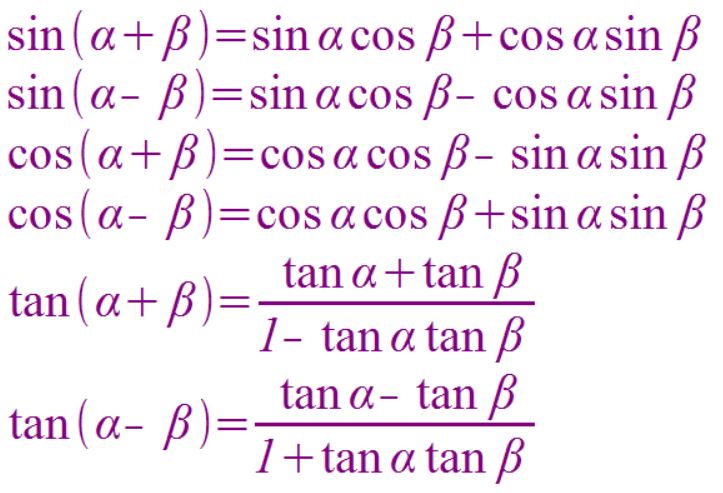1.電力の計測
通常、電力の計測は電圧と電流を測り取ることで可能となります。この二つの値を掛け合わせることで電力の値として計測できることは、「P=VI[W]」の式からも明確です。
さらに交流回路の場合はこれに力率(cosθ)を掛けると有効電力となります。このときの式としては「P=VIcosθ[W]」となります。
ですが、これはあくまで直流回路や単相交流回路での話になります(直流回路に力率の概念はありませんのでご注意ください)。では、三相交流回路ではどのような計測方法になるのでしょうか。この記事では、三相平衡回路における電力の計測について解説していきます。少し数学の知識も必要になりますが、そこは可能な限り丁寧に説明していきます。
数式の読込みにおいてうまく表示できていない場合のために画像も用意しています。クリックやタップで拡大できますのでご活用ください。
2.三相電力でも電圧と電流を計測
前述で、三相電力の計測方法はいったいどのようになるのか、意味深な言い回しをしましたがなんのことはありません。三相回路における電力計測でも電圧と電流を測り取ることになります。では単相交流回路のように一つの相や線間の電圧と一相または一線の電流を測れば勝手に三相回路としての電力計測ができるのでしょうか。
もちろんそうではありません。平衡している三相交流回路で、「力率1」すなわち「cosθ=1」の回路での電力は以下の式になります。なお、添え字の「3p」は単相と区別して三相を表現する意味でつけています。
$(S_{3p}=)P_{3p}=3EI$ [W]
S3p:皮相電力[VA]
P3p:電力[W]
E:電源電圧(相電圧)[V]
I:電流(相電流)[A]
一相分の電力の3倍ということですね。
単純な話ですが、「P=EI[W]」の回路が三つあるので電力も3倍ということです。
さらに力率が1ではない場合はこの値を掛けわせることで有効分の電力が計上されることとなります。その計算式は以下になります。
$P_{3p}=3EI\cos\theta$ [W]
さらにさらに、線間電圧と線電流の組み合わせで計測した場合の計算式としては以下になります。
$P_{3p}=\sqrt{3}V_ℓI_ℓ\cos\theta$ [W]
Vℓ:線間電圧[V]
Iℓ:線電流[A]
3.相電圧や相電流を測る?
先の項目で相電圧や相電流を計測し、それを3倍することで平衡三相回路の電力が計上できることを説明しました。では実際にそのようにして計測されているのでしょうか。答えとしては「そうではない」ということになります。
確かに考えてみると、少しオーバーにはなりますが相電圧や相電流を計測するということは変圧器(トランス)や電動機(モーター)内部に計測用機器(の一部)を埋め込まなければならないということになります。
それはやはり現実的ではないですね。
三相電力の計測において「相」という概念が存在する限り、上記のようなに単純に3倍するだけの方法では少し無理があるということがわかります。そこでこれまでに編み出された計測方法に「二電力計法」というものがあります。この計測方法について解説していきます。
4.二電力計法で三相電力計測
二電力計法は三相電力を計測するメジャーな方法です。二つの単相用電力計器で三相電力を計測できるというなんとも魔法のような計測方法ですが、ちゃんと理にかなっています。
ではこれについて理論から説明していきます。なお、この記事では平衡三相交流回路に的を絞って説明していきます。
1)平衡三相回路の電圧電流ベクトル
二電力計法では「ベクトル合成」によってその電力が計上されます。「ベクトル合成」って何?と思われる方もおられるかもしれませんがここでの説明を読み進めていただければ充分理解してもらえるかと考えます。
以下にa相,b相,c相の相電圧と相電流をベクトル図で表します。
これが各電圧電流のベクトルであり、図示されている各々の矢印が一定の回転速度でくるくる回っていると考えてください。
上記の図ではこの後に説明する計測の結線を見越して、Ea[V]とIa[A]及びEc[V]とIc[A]の位相差についてのみ言及していますが、もちろんEb[V]とIb[A]でもθ°の位相差があります。電圧でも電流でも生じている角度の差を位相差と呼ぶことは力率の理解~交流回路で必須の知識~でも解説しています。
そしてこれらのベクトルを合成していくことで平衡三相電力の計上ができるということです。
2)ベクトル合成のための計器接続
上記のベクトル図は単純に相電圧と相電流についての各相を表現したのみにすぎません。これから三相回路に計器を接続することで各相の電圧ベクトルが合成されることとなり、そこから平衡三相電力計測が可能となります。
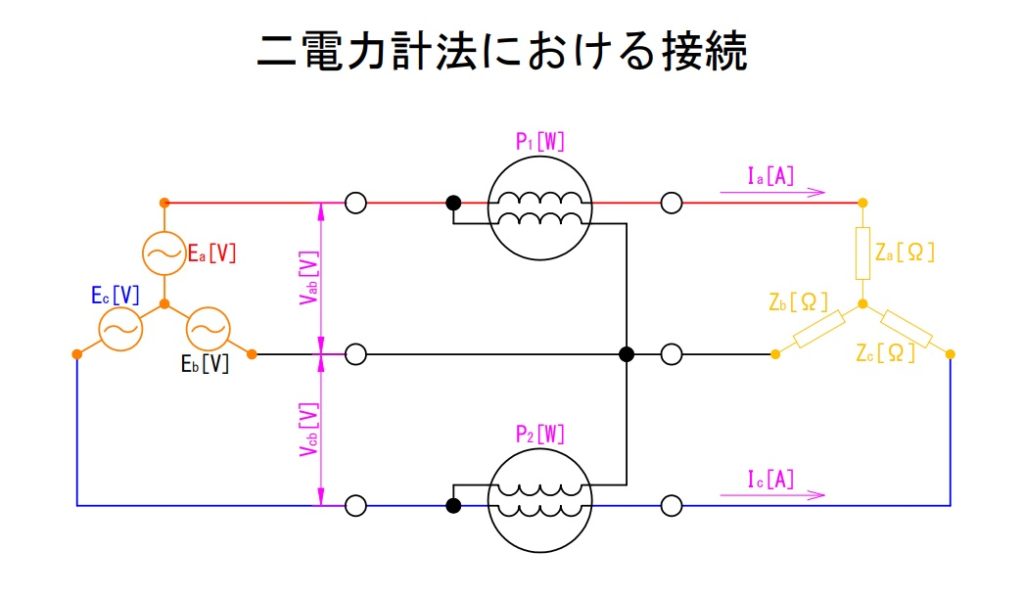
以下は平衡三相回路の電力を二電力計法により測り取るための計器接続図です。この接続により後述のベクトル合成となります。
3)接続によるベクトル合成
前述の計器接続による電圧ベクトルの合成状態が以下の図になります。これにより測り取られる一相ごとの電力の値は以下のようになります。ここで注意すべきはb相の電圧に関しては逆のベクトルを合成してることです。これは、先の接続図においてa-b間,c-b間のいずれもb相にとっては逆向きの電圧であることが起因しています。
なお、a相(ab相間)に接続した計器で測り取った電力をP1[W]とし、c相(cb相間)に接続した計器で測り取った電力をP2[W]とします。
$P_1=V_{ab}I_a\cos(30°+\theta)$ [W]
$P_2=V_{cb}I_c\cos(30°-\theta)$ [W]
合成された結果を各々足し合わせることで最終的に平衡三相電力となります。
5.三角関数の利用
ベクトルの合成までできるとあと一息で平衡三相回路での電力算出ができます。ここで、新たな数学の知識が必要になります。
三角関数という項目なのですが、これを聞いただけでアレルギー反応を起こしてしまう方も少なくないかと思います。ですが、ここでは三角関数の基礎と加法定理の一部しか使いませんのでご安心を!
さらに、実用の方面からこのような数学に触れていきますのでその必要性も理解できる機会としてとらえてもらえると非常にありがたいです。
では説明します。
1)加法定理の利用
三角関数の角度を足し合わせる場合は、加法定理なるものの公式に従って計算します。例えばsin(θ1+θ2)はsinθ1+sinθ2とはなりません。ではどうすべきなのか、公式を以下に記載します。
$\sin(α+β)$
$=\sinα\cosβ+\cosα\sinβ$
$\sin(α-β)$
$=\sinα\cosβ-\cosα\sinβ$
$\cos(α+β)$
$=\cosα\cosβ-\sinα\sinβ$
$\cos(α-β)$
$=\cosα\cosβ+\sinα\sinβ$
$\tan(α+β)=\frac{\tanα+\tanβ}{1-\tanα\tanβ}$
$\tan(α-β)=\frac{\tanα-\tanβ}{1+\tanα\tanβ}$
2)一相ごとの電力足し合わせ
では上記三角関数も活用し、計器で測り取った一相ごとの電力を足し合わせていきます。可能な限り丁寧に記述していきます。前提条件として以下がありますのでこちらもおさえておいてください。
$V_{ab}=V_{cb}=V_ℓ$ [V]
$I_a=I_c=I_ℓ$ [A]
この条件下で計算していきます。
$P_1=V_{ab}I_a\cos(30°+\theta)$
$=V_ℓI_ℓ\cos(30°+\theta)$ [W]
$P_2=V_{cb}I_c\cos(30°-\theta)$
$=V_ℓI_ℓ\cos(30°-\theta)$ [W]
※P1とP2を足し合わせる
$P_1+P_2$
$=V_ℓI_ℓ\cos(30°+\theta)$
$+V_ℓI_ℓ\cos(30°-\theta)$ [W]
※ここで加法定理を適用
$P_1+P_2$
$=V_ℓI_ℓ(\cos30°\cos\theta$
$-\sin30°\sin\theta)$
$+V_ℓI_ℓ(\cos30°\cos\theta$
$+\sin30°\sin\theta)$ [W]
※これを以下のように展開
$P_1+P_2$
$=V_ℓI_ℓ\cos30°\cos\theta$
$-V_ℓI_ℓ\sin30°\sin\theta$
$+V_ℓI_ℓ\cos30°\cos\theta$
$+V_ℓI_ℓ\sin30°\sin\theta$ [W]
※「-VℓIℓsin30°sinθ」と「+VℓIℓsin30°sinθ」は打ち消される
$P_1+P_2$
$=V_ℓI_ℓ\cos30°\cos\theta$
$+V_ℓI_ℓ\cos30°\cos\theta$ [W]
$P_1+P_2$
$=2V_ℓI_ℓ\cos30°\cos\theta$ [W]
※$\cos30°=\frac{\sqrt{3}}{2}$
$P_1+P_2=2V_ℓI_ℓ・\frac{\sqrt{3}}{2}・\cos\theta$ [W]
$P_1+P_2=\sqrt{3}V_ℓI_ℓ\cos\theta$ [W]
※よって三相電力は以下となる
$P_{3p}=P_1+P_2=\sqrt{3}V_ℓI_ℓ\cos\theta$ [W]
上記で導き出された式が「2.」で記載されている式と同じになりました。つまり、平衡三相回路において二つの単相用電力計器で平衡三相電力を計測できるということになります。
6.二電力計法のメリット(知見)
これまで二電力計法により平衡三相回路での電力が計測できることがわかりました。そして実際にこの計測方法は多く利用されています。
ですが、結構計算が面倒であり理解するにも時間がかかりますよね。ではなぜこのような方法が多く使われているのか筆者なりに考えてみました。以下のようなメリットがあると考えられます。
・線間電圧,線電流での計測が可能。
・電流センサー2個で済む。
・センサー数が少なくなることで接続配線も少なくなる
上記が筆者の考えるメリットです。
また、別のメリットとして、この二電力計法は電気数学の理解にもうってつけの方法です。実際、筆者もこの項目の学習を通じて「ベクトルとはどういうものなのか」や「三角関数の活用」について理解が深まったと感じています。
「三角関数他、数学なんて生きていくうえでどう必要なの?」の疑問も少なからず解決してくれました。
学習中の皆さんにもこの解説が大いに役に立てば幸いです。