1.電気回路の計算は難しい?
皆さんは電気回路計算にどのような印象を抱いておられるでしょうか。
「難しい」や「理解しにくい」などの印象も多いことでしょう。物事は分野を問わず深く知れば知るほどレベルは大きく上がり、求められる理解も難しくなっていきます。しかし、【○○界の権威】を目指す場合を除き、でもプロとしてやっていく場合において、ひととおりの理解で充分な場合の方が圧倒的に多いと筆者は考えます。
もちろん知識・理解が多く深いに越したことはありませんが、筆者がもっと大事だと考えるのは「自身の理解度を把握」し「逐次不足している知識を吸収していく」ことです。先ずは基礎や基本といわれることを押さえておき、そこから実務レベルまで引き上げることができればあとはそのときそのときにおいて不足しているものを取込んでいくことのみで多くの問題が解決すると考えます。
そしてその基礎・基本を押さえることに最もエネルギーが必要となります。これは筆者の経験と周囲を観察した結果から言えることです。
「"0"から"1"」が最も精神的にきついと感じますが、"1"を"2"へ、"2"を"10"へという工程は「"0"から"1"」のときより多少楽になるのではないでしょうか。そしていつしか"100"になったときに、そこからの"101","102"へのステップはまた大きなエネルギーを必要とすると考えます。
というわけで、今回は電気回路の計算における簡単なところから解説をし、なんとか「"0"から"1"」の段階でなるべく不要なエネルギーを費やさないためのコツを紹介できればと思い、記事にまとめます。
2.電気回路計算のコツとは
では、電気回路計算に「コツ」なんてあるのでしょうか?
筆者はそれに類するものは「ある」と思っています。これまで、凡人の筆者がある日「ああ、そうか!」と理解したときに掴んだそれは「同じもの探し」ということです。
1)「同じもの探し」とは
ここでいう「同じもの探し」とは「同じ電圧(電位差)」や「同じ電流」,「同じ負荷」等です。これを探し出せれば計算に大いに役立ちます。以下に単純な例を載せます。
a.同じ電圧
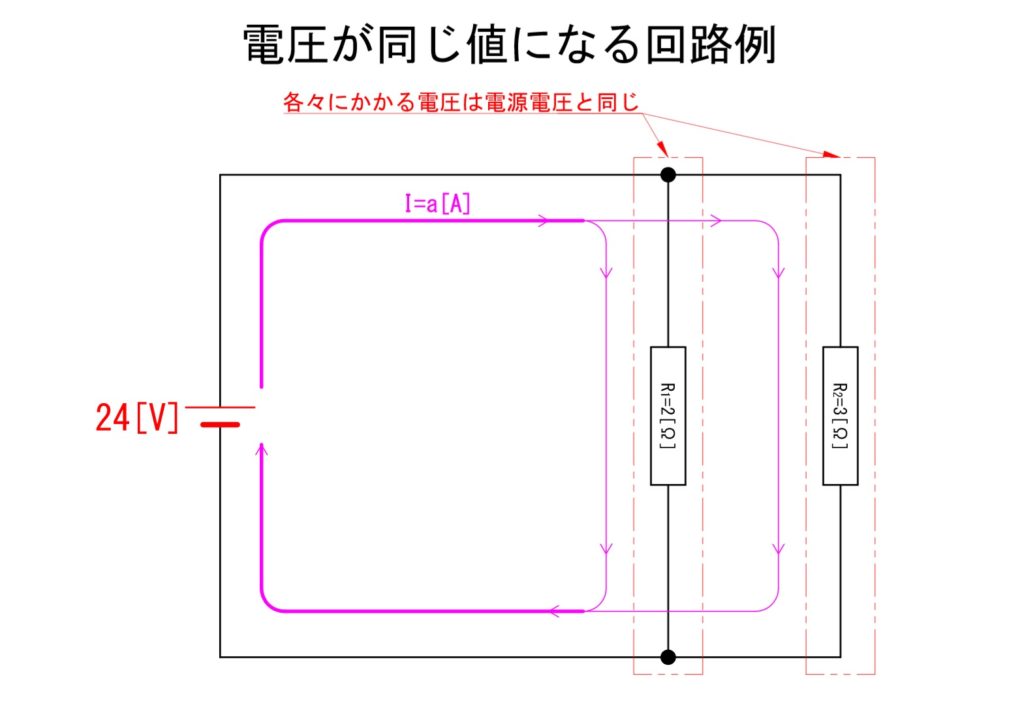
先ずは「同じ電圧」探しです。下の図では抵抗;R1[Ω]と抵抗;R2[Ω]が並列に接続されています。同じ電圧を探して回路の全電流I;[A]を算出してみましょう。
すでに図の中には記載されていますが、この回路の場合、R1[Ω]とR2[Ω]にかかる電圧は電源電圧と同じになります。このコツを理解しているかどうかが計算のやりやすさに大きく関与します。
理由は合成抵抗計算をするか否かにあります。王道はおそらく、合成抵抗を計算しオームの法則から電流計算をする方法でしょう。しかし、「R1[Ω]とR2[Ω]にかかる電圧が電源電圧と同じになる」ことを瞬時に見抜ければ単純な割り算と足し算で計算できます。
実際に上の図の全電流;I[A]計算をします。
R1=2[Ω]で、ここにかかる電圧はV1=24[V]ですので、R1[Ω]に生じる電流;I1[A]を計算すると以下になります。
①I1 = 24/2 = 12[A]
R2=3[Ω]で、ここにかかる電圧はV2=24[V]ですので、R2[Ω]に生じる電流;I2[A]を計算すると以下になります。
②I1 = 24/3 = 8[A]
電流;I1[A]と電流;I2[A]を足し合わせた結果が全電流;I[A]です。
③I = 12+8 = 20[A]
ということで回路に生じる全電流は20[A]という結果が出ました。
これを合成抵抗から求めても同じ電流値になりますが、計算が単純な分上記での方法の方が素早く結果を出せます。「同じ電圧」を探し出せたことで、回路計算を暗算でできるレベルまで引き落としてくることができましたね。
b.同じ電流
続いて「同じ電流」探しです。
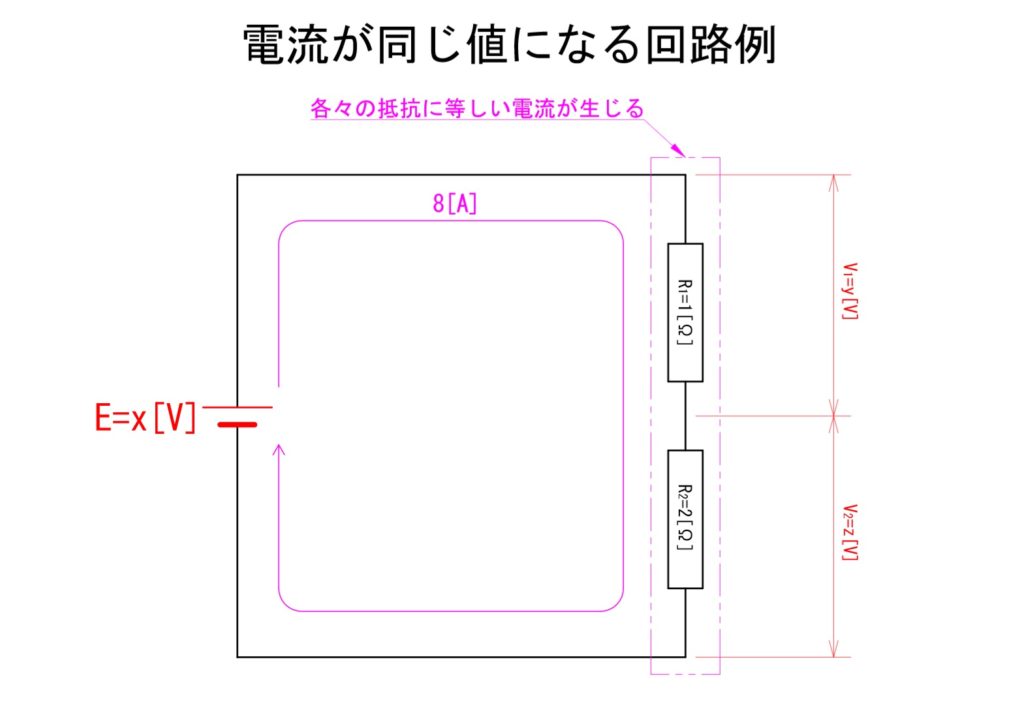
下の回路における電源電圧と各抵抗にかかる電圧を算出してみましょう。
抵抗;R1[Ω]と抵抗;R2[Ω]は直列に接続されています。こちらもすでに図の中には記されていますが、直列に接続された抵抗では同じ電流値となります。
実はこれ、意外と感覚で掴みづらいところなのです。抵抗とは電気の通り難さですから、小さい抵抗と大きい抵抗ではそれらに生じる電流は違うと思いがちです。しかし直列接続においては同じ電流値となります。
下の図の回路で、電源電圧を算出するのは合成抵抗算出後でもなんら問題ありませんが、R1[Ω]にかかる電圧;V1[V]とR2[Ω]にかかる電圧;V2[V]を算出する場合は「同じ電流」であることを利用するとすぐに算出できます。
以下、上の図の回路における各電圧の計算です。合成抵抗を算出しない方法を用います。
全電流をI[A]とすると、R1[Ω]に生じている電流は全電流と同じくI=8[A]ですので、そこにかかる電圧V1[V]は以下となります。
①V1 = 8×1 = 8[V]
全電流をI[A]とすると、R2[Ω]に生じている電流は全電流と同じくI=8[A]ですので、そこにかかる電圧V2[V]は以下となります。
②V2 = 8×2 = 16[V]
電源電圧E[V]は電圧;V1[V]と電圧;V2[V]を足し合わせた結果となります。
③E = 8+16 = 24[V]
ということで電源電圧は24[V]、R1[Ω]にかかる電圧V1[V]は8[V]、R2[Ω]にかかる電圧V2[V]は16[V]という結果が出ました。
これもまた、瞬時に計算が完了しました。
電験など難関資格取得は通信教育もアリ!
思い立ったが吉日!即行動で合格!!
![]()
3.複雑になっても「同じもの探し」は役立つ
先程まではかなり基本的な単純な回路における計算でしたが、回路が少し複雑になってもこの「同じもの探し」は役に立ちます。
その例を以下に挙げます。目的の計算ができるかみていきましょう。
1)回路例1
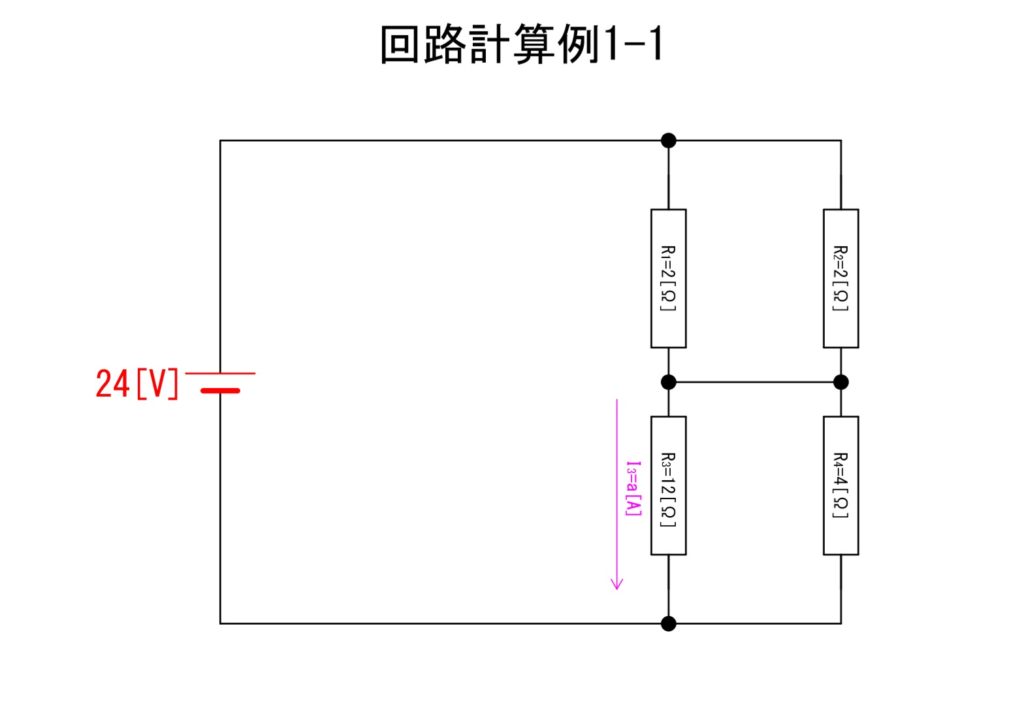
下の「回路計算例1-1」の図におけるI3[A]について、同じものを探しながら算出する工程を解説します。
a.先ずは合成抵抗算出
先ずは、R1[Ω]とR2[Ω]の合成抵抗;R12[Ω]とR3[Ω]とR4[Ω]の合成抵抗;R34[Ω]を各々算出します。以下、計算式です。なお、繁分数の分母部分にある分数につけた括弧はわかりやすさのためのものですので、本来不要です。ご注意ください。
①R12 = 1/{(1/2)+(1/2)} = 1[Ω]
②R34 = 1/{(1/12)+(1/4)} = 3[Ω]
b.さらに合成抵抗算出
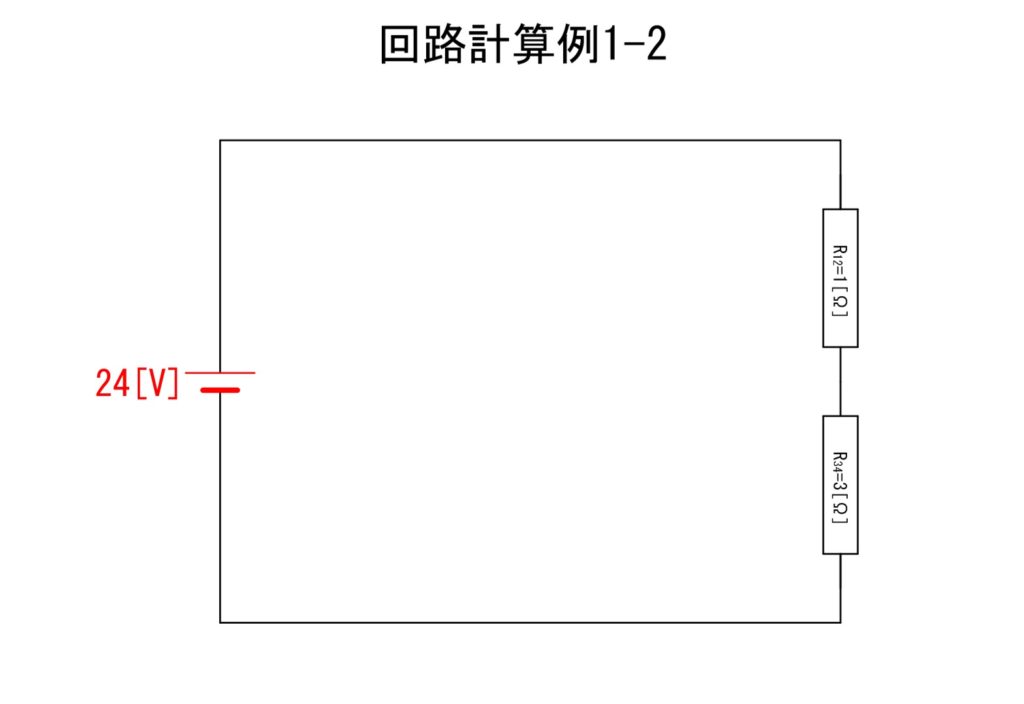
計算結果から図は「回路計算例1-2」のようになります。
さらに合成抵抗;R0[Ω]を算出します。といっても足し合せるだけですね。
③R0 = 1+3 = 4[Ω]
c.全電流算出
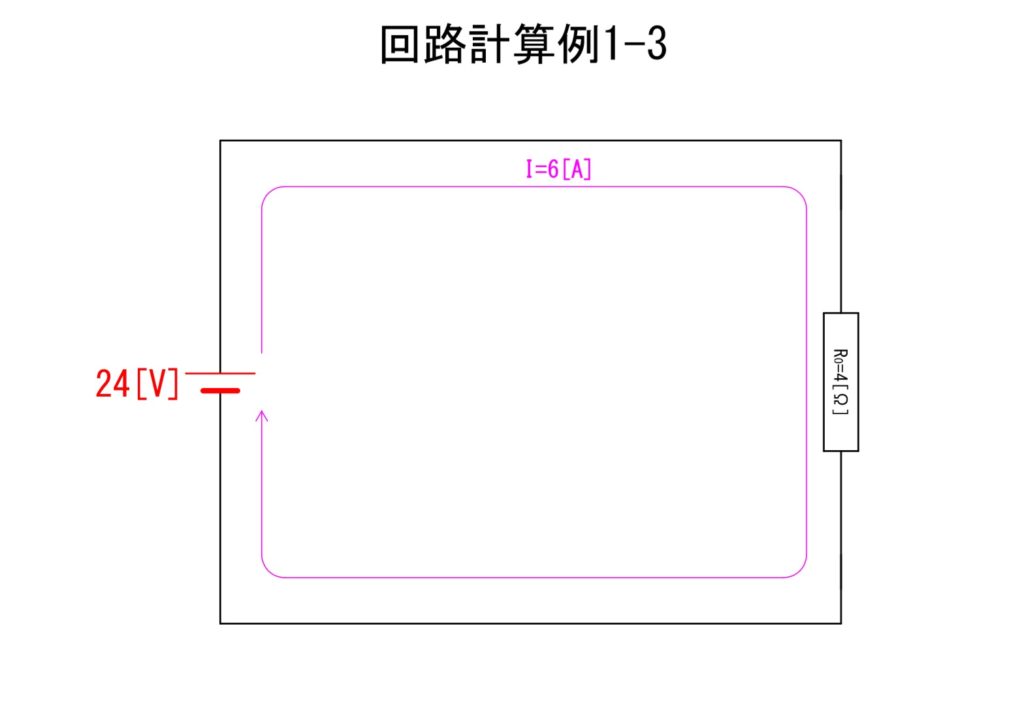
その結果回路は「回路計算例1-3」のように単純化されます。
そしてオームの法則から全電流;I=6[A]が算出されます。
d.各並列接続部の電圧算出
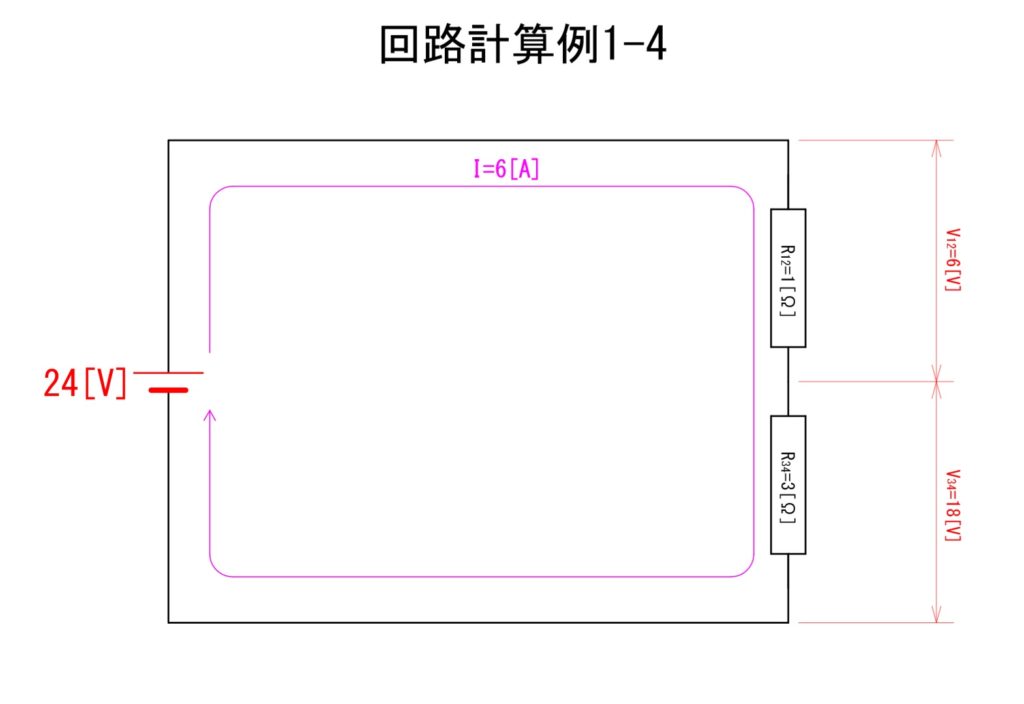
今度は、再びR12[Ω]とR34[Ω]の回路に戻します。ここで、直列接続の各抵抗に生じる電流が同じであることを利用して各々の抵抗にかかる電圧が算出できます。「回路計算例1-4」でのV12[V]とV34[V]の算出は掛け算で可能です。
④V12 = 6×1 = 6[V]
⑤V34 = 6×3 = 18[V]
各々にかかる電圧が算出できました。
e.各抵抗に生じる電流算出
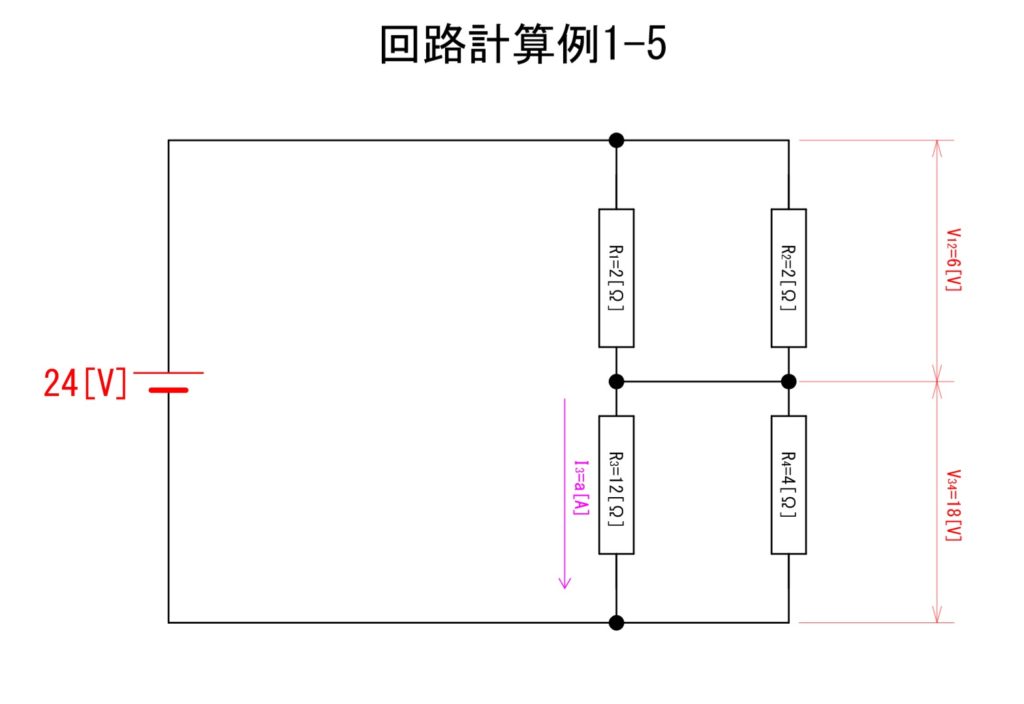
ここで元の回路と算出した電圧を見比べてみます。「回路計算例1-5」にあるとおり、並列接続の抵抗には同じ電圧がかかります。これを利用するとオームの法則で各抵抗に生じる電流が算出できます。念のため全ての抵抗に生じる電流を計算してみます。
R1[Ω]に生じる電流をI1[A]、R2[Ω]に生じる電流をI2[A]、R3[Ω]に生じる電流をI3[A]、R4[Ω]に生じる電流をI4[A]として算出します。
⑥I1 = 6/2 = 3[A]
⑦I2 = 6/2 = 3[A]
⑧I3 = 18/12 = 1.5[A]
⑨I4 = 18/4 = 4.5[A]
今回欲しい値はI3[A]ですので結果は⑧式から1.5[A]となります。
2)回路例2
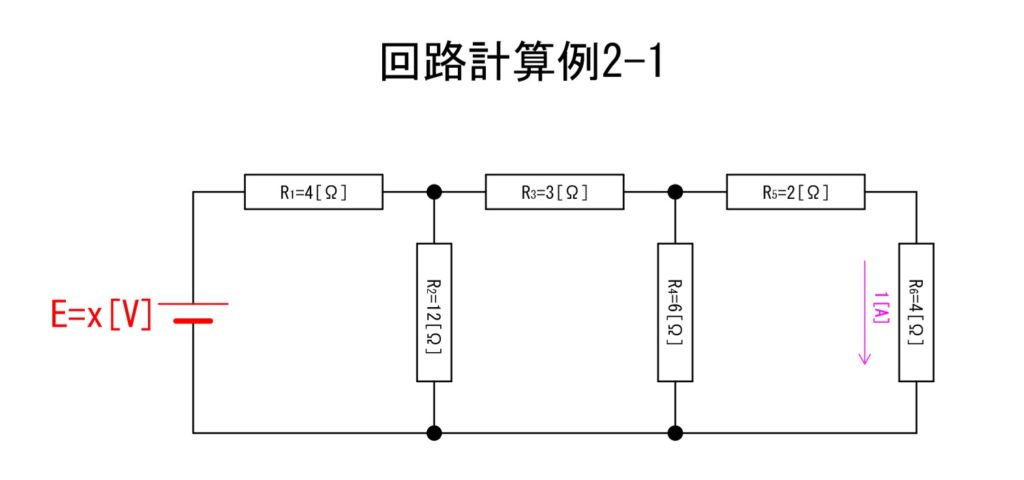
下の「回路計算例2-1」の図における電源電圧;E[V]について、同じものを探しながら算出する工程を解説します。条件は図にあるとおりで各抵抗値とR6[Ω]に生じる電流が1[A]であるということが既知です。オームの法則とキルヒホッフの法則(第一法則=電流則)を利用します。
一見複雑に見える回路ですが、並列接続になっている回路を探していけば同じ電圧として扱うことができ、丁寧に計算することで簡単に算出できます。
a.同じ電流が生じる場所
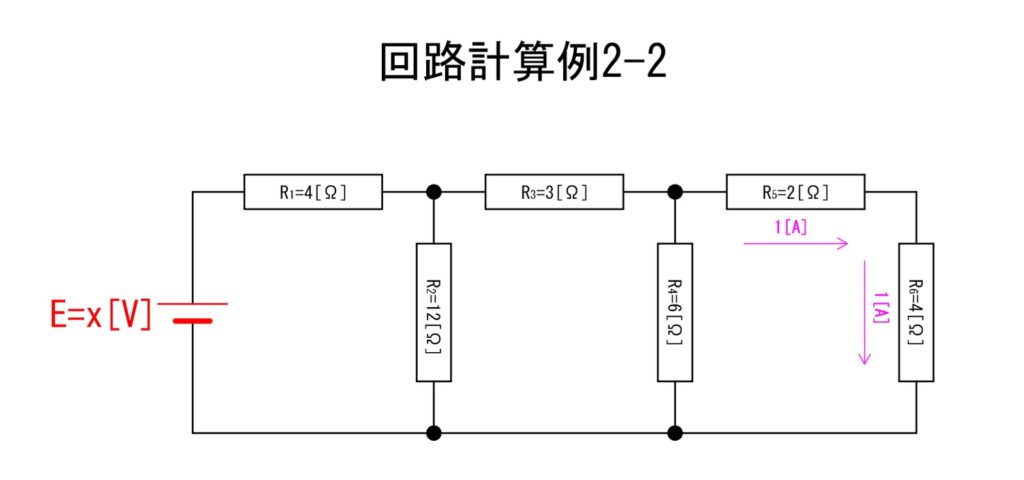
先ずはR6[Ω]に生じる電流が1[A]ということからR5[Ω]に生じる電流も同じ1[A]であることがすぐにわかります。
b.電圧算出①
「回路計算例2-2」にはR5[Ω]に生じる電流を記載しました。
R5[Ω]とR6[Ω]に生じる電流が各々1[A]であることからここにかかる電圧を以下の計算式から算出できます。V56[V]とします。
①V56 = 1×(2+4) = 6[V]
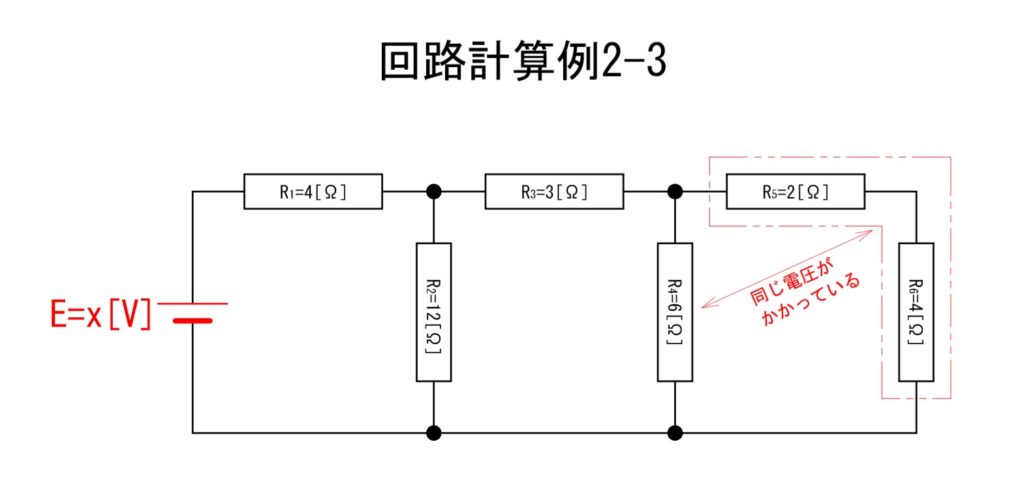
c.同じ電圧があらわれる場所①
ここで算出された電圧;V56[V]はR4[Ω]にあらわれる電圧と同じです。「回路計算例2-3」に図示します。つまりR4[Ω]には6[V]がかかっているということです。
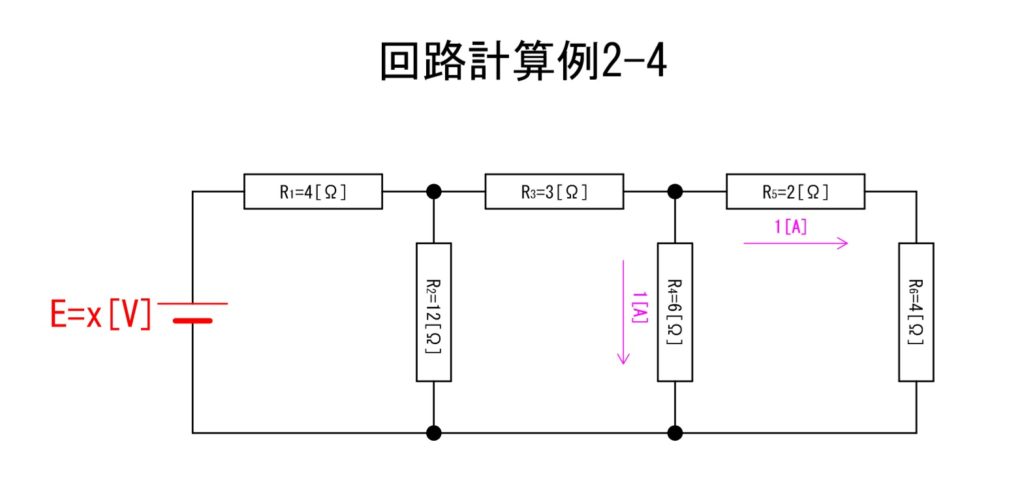
d.電流算出①
R4[Ω]には6[V]がかかっていることから生じる電流;I4[A]が算出できます。以下、計算式です。
②I4 = 6/6 = 1[A]
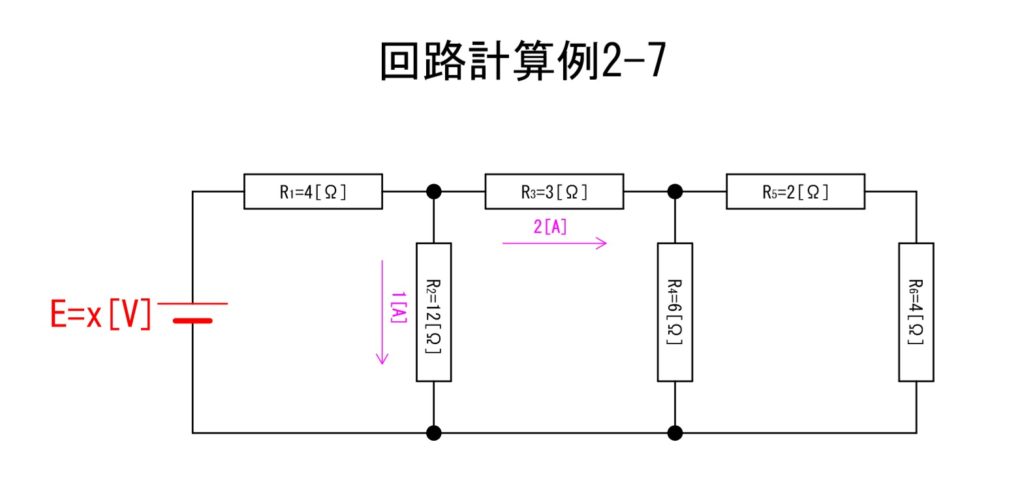
ここで、キルヒホッフの第一法則の「流入電流と流出電流が等しい」ことからR3[Ω]に生じる電流;I3[A]が算出できます。
③I3 = 1+1 = 2[A]
R3[Ω]とR4[Ω]に生じる電流が算出できました。
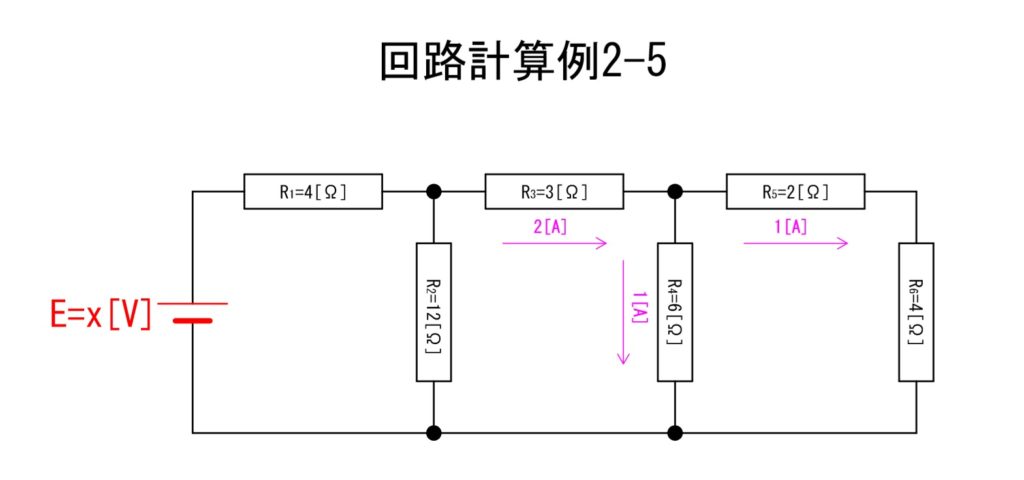
e.電圧算出②
R3[Ω]にはキルヒホッフの第一法則から2[A]の電流が、R4[Ω]には1[A]の電流が生じていることから、ここにかかる電圧を以下の計算式で算出できます。V34[V]とします。
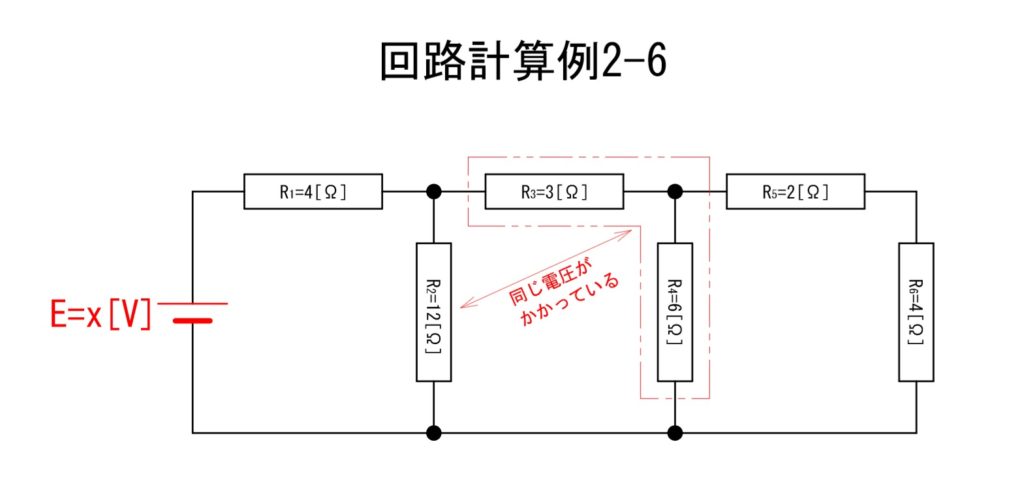
「回路計算例2-6」の赤い二点鎖線が囲う位置の電圧;V34[V]の算出式は以下のとおりです。
④V34 = 2×3+1×6 = 12[V]
f.同じ電圧があらわれる場所②
V34[V]はR2[Ω]にあらわれる電圧と同じですので、R2[Ω]に生じる電流もオームの法則から算出できます。
⑤I2 = 12/12 = 1[A]
g.電流算出②
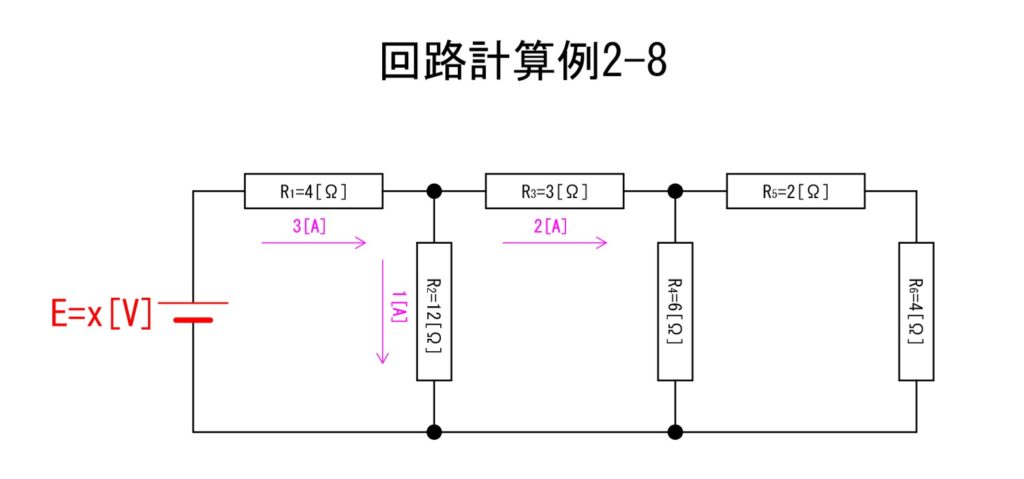
再び、キルヒホッフの第一法則からR1[Ω]に生じる電流;I1[A]が算出されます。
⑥I1 = 1+2 = 3[A]
R1[Ω]とR2[Ω]に生じる電流が算出できました。
h.電圧算出③
R1[Ω]には3[A]、R2[Ω]には1[A]が生じているということになります。ここにかかる電圧を以下の計算式で算出できます。V12[V]とします。
⑦V12 = 3×4+1×12 = 24[V]
i.電源電圧の算出完了
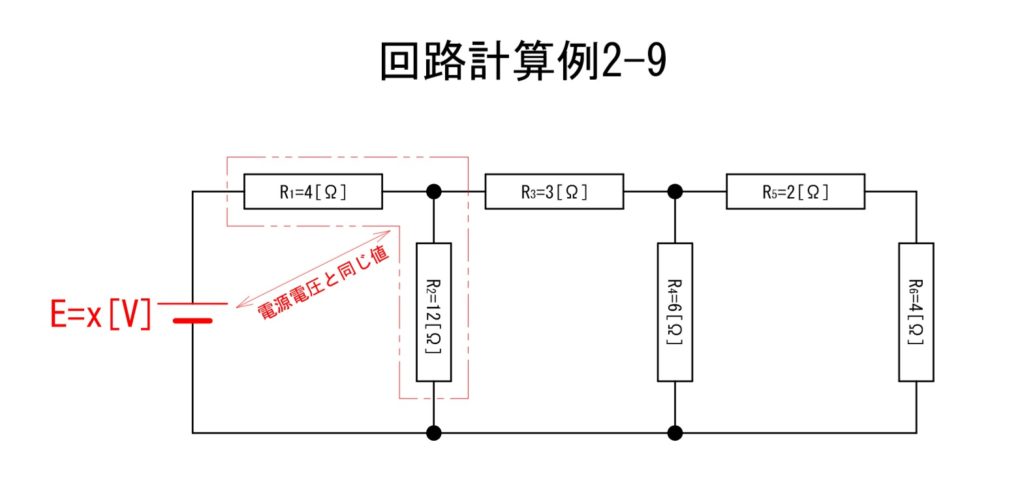
「回路計算例2-9」の赤い二点鎖線が囲う位置の電圧;V12[V]は電源電圧;E[V]と同じになります。
⑧V12 = E = 24[V]
以上、24[V]がこの回路での電源電圧となります。
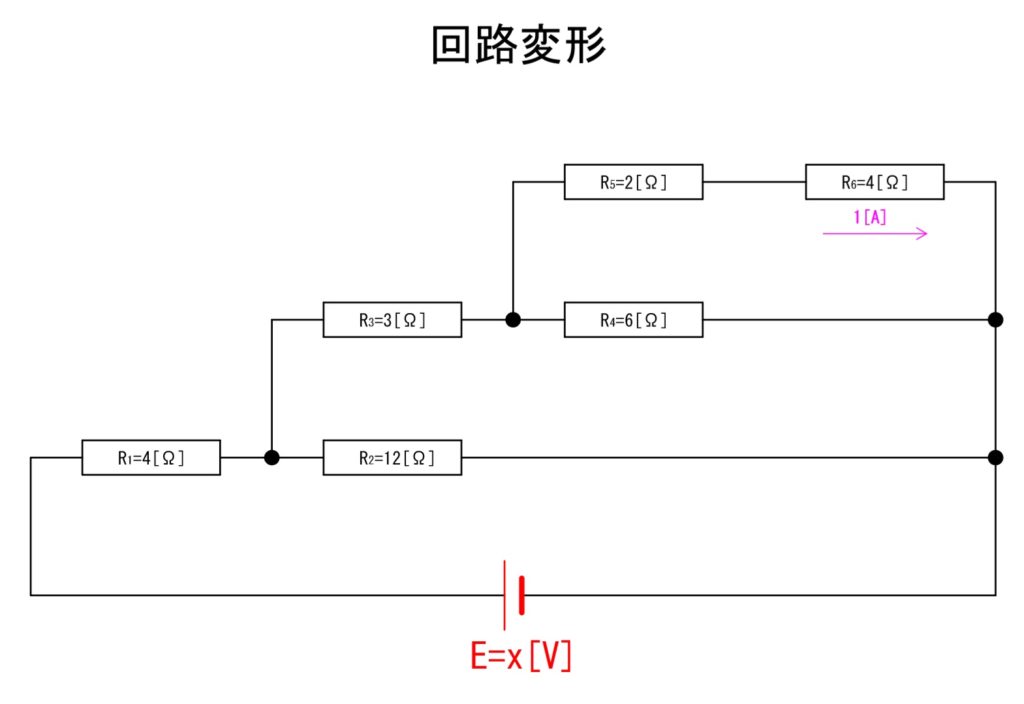
j.回路変形(より考えやすく)
ちなみに参考ですが、この回路を等価のまま変形した図を以下にのせておきます。こうすることで並列接続が見やすくなるとおもいます。
4.回路の理解を深めていく
以上、電気回路計算における要領をコツ的なものと一緒に解説しました。試験でも実務でも、回路をじっくりみることで、目的とする数値を容易に算出できる場合も多く存在します。そのためには電気回路における現象や性質を知っておく必要があります。
電気回路を理解するためにはより多くの電気図面をみてよんでいくこととその実配線を見比べていくことが近道なのではないかと考えます。最初はよくわからない状態でも不明点をひとつづつ消化していくことで知らぬ間にそのスキルは向上します。同じ意味の図面でもだれがひいた図なのかどの企業,メーカーでの図面なのかで表現も異なる場合があります。それすらも戸惑うことなく読めていけるようになれば電気に関する知識が深まっている証拠です。
もちろん回路に限らず、電気のエネルギーとしての現象や性質もひとつひとつ着実に理解を深める必要もあります。学び始めの方はまだまだ先が長いように感じるでしょうが焦る必要はありません。着実に学習等を継続していくことで自身の成長が手に取るようにわかる時期が必ず来ます。
筆者も知識と経験の積み重ねを止めるつもりは全くありません。一緒に頑張りましょう!