1.短絡電流は算出可能
電気事故の代名詞的な現象として「短絡事故」というものがあります。これは電路に接続された機器やその接続に使用する配線などを過熱させ破壊する非常に危険な現象です。このときの被害は電路上の機器や配線にとどまらず、建造物の焼損に至ることもあります。
短絡と漏電の記事でも説明していますが、短絡事故時の電流値はキロアンペア([kA])クラスにもなります。これは、電源からみた短絡点までのインピーダンスが電圧に対して非常に小さいために生ずるものとなります。短絡事故においてインピーダンスが非常に小さくなる理由は、対極が負荷を介さずに電気的に接触してしまうことに起因します。
1)単純なオームの法則で算出可能?
ではこの短絡電流、あり得ないほどの電流値ということですが、いったいどれほどの値なのでしょうか。事故によるものなので、もはや算出など不可能ではないかと考える人も少なからずいるでしょう。しかし短絡電流による電気事故と言えど物理現象であり、電気理論の範疇をこえることはありません。ですので、有名な電気の法則であるオームの法則などを用いて算出可能です。
ただし短絡電流の発生時はなにも純抵抗のみの場合とは限りません。というよりも、コイルなどによるリアクタンスの成分が多く含まれることがほとんどです。ですので負荷についてはインピーダンスとしての値を用います。その部分以外はオームの法則の適用となんら変わりはありません。短絡電流を「IS [A]」として以下に式を記載します。

なにも特別なものでもないということがわかります。短絡が発生した回路での電圧と短絡点までのインピーダンスがわかれば、たとえ短絡電流のような大きな値でも算出できるということです。
2)関係あるのはインピーダンス
短絡事故時の大きな電流値であってもオームの法則で算出することが可能ということはわかりましたが、現実的に算出する場合そのような単純なものなのでしょうか。
結論から言うと、厳密に算出しようとするのであれば面倒な手順をたどる必要があります。理由は簡単で、先ほどから出てきている「インピーダンス」が関係してくるからです。インピーダンスが関係する電気的数値の算出にはその多くで「複素数」での計算が必要となります。これが関わってくるだけで計算は複雑になり難易度が大きく上昇します。例えば変圧器と配線の合計インピーダンスを算出するだけでも実数と虚数に分けて考える必要があり、さらにその大きさについては「三平方の定理」が必要となります。このことは抵抗,コイル,コンデンサ〜インピーダンス〜の記事で説明していますのでこちらも参照してください。
系統の電圧や容量が変化する場合などでは、なおのことインピーダンスが関わることによる計算の複雑化が顕著になります。
2.パーセントインピーダンス(%Z)法
前述のような理由から、算出工程が複雑になるインピーダンスが関わる計算ですが、こと変圧器などにおける短絡電流に関しては簡略化した計算方法があります。「パーセントインピーダンス(%Z)法」という考え方です。用いられるシーンとしては変圧器を含む電源回路等においてです。これによる複雑さの回避には目を見張るものがあります。先人の知恵というものは凄いですね。
ではこれから上記にある複雑さ回避の計算方法であるパーセントインピーダンス法について説明しますが、これには前提条件があります。「抵抗成分がリアクタンス成分に比べ無視できるほどに小さい」ということです。これがパーセントインピーダンス法が前述の「変圧器などの短絡電流算出」で有利となる条件でもあります。抵抗の値が無視できないくらいの大きさである回路ではパーセントインピーダンス法による計算であっても複素数による計算を避けて通ることはできません。とはいえ、このパーセントインピーダンス法が用いられるのは変圧器とそこに接続される配線に関してがほとんどですので大きな抵抗成分が絡んでくることはあまり考えなくても良いです。
1)%Z法の公式
パーセントインピーダンス法における公式を以下に記載します。基本公式は以下ですが、この式から複数の別の式へと導出が可能です。公式が説明しているのは「相電圧に対する電圧降下の割合(百分率)」です。このときの「Z [Ω]」は変圧器の内部インピーダンスや配電線のインピーダンスを表しています。負荷のインピーダンスではありませんので注意してください。
パーセントインピーダンスの数値の意味は、定格電流が生じている回路上での内部インピーダンスによる電圧降下を相電圧で除した値、すなわち「比」となります。文字におこせば少しややこしいですが数式にしてみるとなんのことはありません。
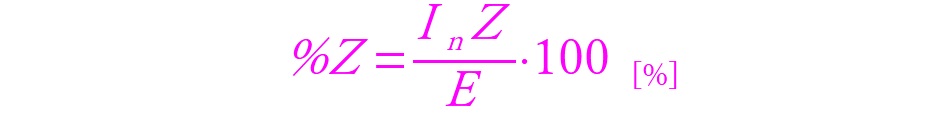
%Zが明らかである前提で、電圧や容量がわかっている場合または電圧やインピーダンスがわかっている場合など条件に応じて各種数値の算出に利用できる、非常に扱いやすい便利な式です。
2)容量に比例
パーセントインピーダンスは変圧器などの容量に比例します。このことにより、インピーダンスが関係する計算であっても必要以上に複雑にならずに済むということです。
ですが、いきなり「容量に比例」などといわれてもなぜそのような考え方が必要であるのかについて根拠が欲しいところです。そしてこのことは短絡電流他を算出する際に非常に大切な事項となります。
ではなぜ「容量に比例」するのかについて説明します。
例えば、変圧器が複数台で負荷に電源供給している回路においてその二次側で短絡がおきた場合の短絡電流を算出するとき、各変圧器の%Zを単純計算するわけにはいきません。なぜ単純計算では成立しないのかについては以下の式で明らかです。以下の式は前述のパーセントインピーダンスの式を変形したものになります。この変形導出に関しては後述します。
非常に単純な式ですがここにとても大切な要素が含まれていることを理解してください。なお、パーセントインピーダンスは変圧器などが主体となりますのでそれらの容量を「P[VA]」として表しています。また電圧の記号においては端子電圧の「V[V]」を使用していますのでここには少し注意が必要です。
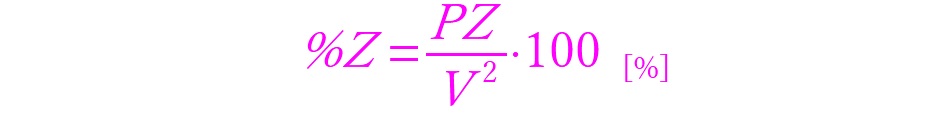
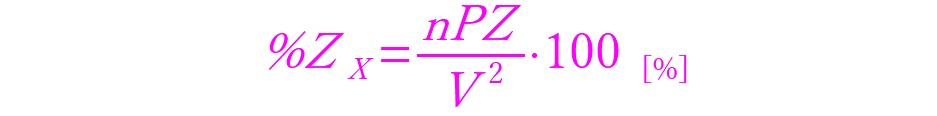
上記において「%Z」を基準としたうえで、例えば変圧器の容量が「n」倍となった時の「%Zx」がどうなるのかについてみていきます。


![]()
上記の式が容量P[W]が「n」倍になった場合のパーセントインピーダンスの変化を表した簡単な式です。これによると容量:P [W]が「n」倍になったならば、パーセントインピーダンスも「n」倍になるということがわかります。式にしてみると、とても単純です。
この過程(容量に比例)を経た後でならばパーセントインピーダンスの数値を単純計算で算出することが可能となります。直列に接続されたものであれば加算で、並列に接続されたものであれば「逆数の和の逆数」で合成抵抗の計算と同じように扱うことができるようになります。もちろん「抵抗成分がリアクタンス成分に比べ無視できるほどに小さい」という前提は外せませんので、これも意識しておくべき条件となります。充分注意してください。
3.短絡電流の算出
前項でパーセントインピーダンスの容量との関係について説明しましたが、そこで説明されていたことを見落とさなければ短絡電流の算出も容易になります。以下に短絡電流を算出するための式への導出とその利用方法について解説します。
1)短絡電流の式を導出
短絡電流の算出について解説します。パーセントインピーダンスの基本公式を変形すると以下のような式を導出することができます。

導出の過程は以下のようになります。まずは「2.1)」で出てきた式の分子分母に「Z」を乗じます。



ここで「IS = E/Z [A]」

短絡電流を算出するための式が導出できました。
2)短絡電流算出
パーセントインピーダンスと短絡電流の関係式を導出できたならば、ここからの短絡電流算出は非常に単純な作業となります。既知のパーセントインピーダンスと定格電流を代入し算出するだけということです。
具体的に短絡電流がどのようになるかを以下の式で表します。
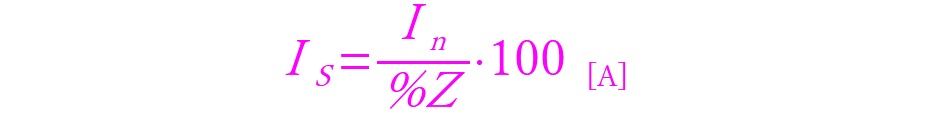
定格電流をパーセントインピーダンスで除するだけですね。非常に簡単です。
4.他要素も算出可能
これまでの説明でも明らかではありますが、パーセントインピーダンス法を用いることで短絡電流だけでなく他の要素も算出が可能となります。ここではその具体例を説明します。
1)容量や電圧
パーセントインピーダンス法から容量や電圧の関係式を導出することが可能です。これは前述の「2.2)」で出てきた式になります。パーセントインピーダンスが既知である前提で、回路の電圧と内部インピーダンスがわかれば容量を算出することが可能となり、内部インピーダンスと容量がわかれば、回路の電圧を算出することができます。まずはパーセントインピーダンスの基本公式です。
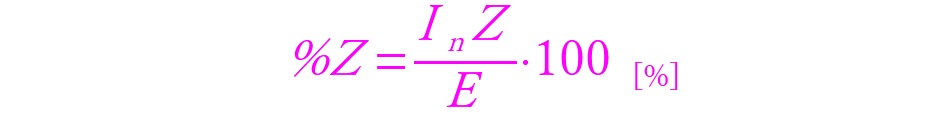
単相交流回路であれば「E=V[V]」ですので以下のようにも書き換えることができます。

この式の分子分母に「V」を乗じます。



ここで「P = VIn [VA]」

容量や電圧に関する式が導出されました。なお、ここでは単相交流回路を例に「P = VIn [VA]」を使用しましたが、三相交流回路での変圧器容量は「P = √3・VIn [VA]」となります。Y結線では「E = V/√3 [V]」,「ILn = IPn [A]」を、Δ結線では「E = V [V]」,「ILn = √3・IPn [A]」を用いれば上記の式が同様に導出されます。「E[V]」は相電圧,「V[V]」は線間電圧,「IPn[A]」は相電流,「ILn[A]」は線電流です。
2)負荷分担からの算出も可能
これまでと同じく抵抗成分がリアクタンス成分に比べ無視できるほど小さいという前提のもとで、変圧器が並列に接続されている場合を考えてみます。この場合でもパーセントインピーダンス法は数値の算出において非常に有効な手段となります。
以下の単線結線図のような系統の回路において、各々の変圧器がどれくらいの負荷を担うのかをパーセントインピーダンス法で算出します。
図内の各変圧器では変圧器AがPA[VA],変圧器BがPB [VA]となっており、各々%ZA[%],%ZB[%]となっています。回路の全電流はI0[A]です。
また変圧器Bは変圧器Aの「n」倍の容量となっています。つまりPB = nPA [VA]ということです。
パーセントインピーダンスは容量に比例するのでまずは各変圧器の容量を同じ値に合わせます。変圧器Aの容量PA[VA]を「n」倍することで変圧器Bの容量PB[VA]と同一になります。
このときの変圧器Bの容量PB[VA]を基準容量といいます。基準容量は任意の値で示される場合もありますが、変圧器自身の容量を基準とする場合は自己容量基準ということになります。
各変圧器Aの容量を基準容量PB[VA]に合わせましたので「2.2)」にあるとおり、%ZA[%]も同様に「n」倍する必要があります。こうすることでn・%ZA[%]と%ZB[%]を通常の抵抗値と同じように扱うことができるということになります。
今回は各変圧器の負荷分担を知りたいということですので分流の式を適用します。変圧器Aが負担する電流値:IA[A]は以下のようになります。
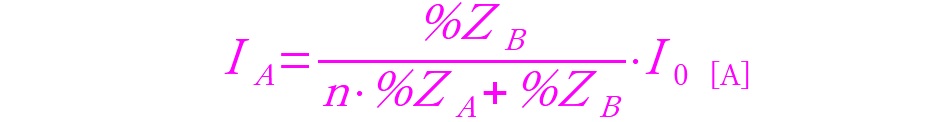
変圧器Bが負担する電流値:IB[A]は以下のようになります。
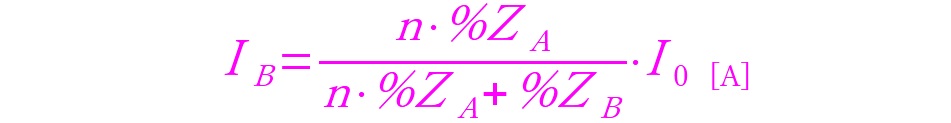
このようにパーセントインピーダンスの値と、これが容量に比例するという法則を利用することで負荷の分担電流を速やかに算出することが可能になります。
3.パーセントインピーダンスと実務
これまでパーセントインピーダンス法により知り得る数値的情報やその導き方について解説してきました。ではこれらの知識は実際の現場ではどのように使われるのでしょうか。パーセントインピーダンスの値がどこに記載されているのでしょうか。そのような実務上の疑問を解決していきます。
1)%Zはどこに?
パーセントインピーダンスの値なんて、知りたくても見たことがないという人も多いのではないでしょうか。実際によく目にするのは変圧器です。変圧器の銘鈑には「短絡インピーダンス」という項目で記載されていることが多いです。
画像の銘板でも短絡インピーダンスという名目で記載があります。赤枠で囲んだ数値がこの記事のテーマであるパーセントインピーダンスと同じ意味となります。
なお、同じ変圧器でも制御盤内で制御電源用に用いられる単相変圧器などではこのような記載はあまりみられません。あくまでも動力や電灯用の変圧器での数値であるようです。
2)計算方法(短絡電流)
銘板にパーセントインピーダンス(=短絡インピーダンス)が記載されていることはわかりましたが、実務上この数値をどう取り扱えば良いのかについて説明します。
「1)」の画像を例に短絡電流を算出してみましょう。上記画像内での数値は「3.5[%]」と記載されています。
この値は変圧器のどのような状態のときのことを言っているのでしょうか。一次側なのでしょうかそれとも二次側なのでしょうか。さらに、基準容量はいくつなのでしょうか。
筆者はこれらのことについて過去に二社ほどに問い合わせをしました。その結果変変圧器銘板に記載されているパーセントインピーダンスの数値は「自己容量基準」であり「一次側も二次側も共通の値を用いる」ということがわかりました。
ですので今回これらの情報をもとに例として一次側の短絡電流を算出してみます。これはどれくらいの遮断容量をもつ遮断器を選定や配線の短時間許容電流の算出などに役立ちます。
まず変圧器一次側の定格電流を算出します。以下の式から定格電流を求めます。
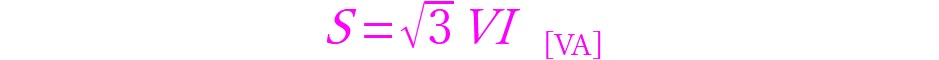
容量:Sは銘板の画像から200×103[VA]であり、電圧:Vは3300[V]であることがわかります。このことから以下のように数値を代入します。

これを解きます。
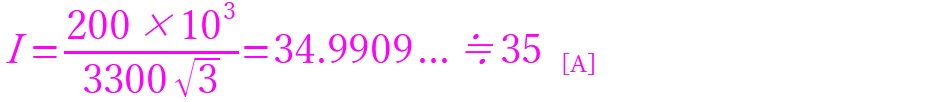
実はこのことは銘板にも記載があります。「定格電流 一次」という項目で値としては計算結果と同じ35[A]が記載されています。
一次側の定格電流がわかれば、あとはパーセントインピーダンスの値で除するのみで短絡電流が算出できます。下に再度公式を記載するとともに計算も記載します。
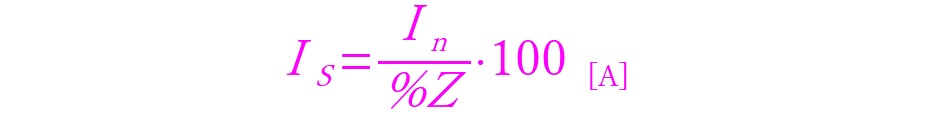
上記の式に各々の値を代入します。Inは35[A]です。%Zは自己容量基準ですのでこのまま利用できます。ですので3.5[%]をそのまま代入することが可能です。

![]()
上記から変圧器における短絡電流が算出されました。
これをもとに遮断器における遮断定格の決定や配線の短時間許容電流の算出などが可能となります。もちろんこれだけではなく配線のインピーダンスなどが絡んでくる場合などパターンはいくつもあります。回路の構成には充分注意が必要です。
4.電気保安のために
今回は短絡電流を中心にその算出方法のひとつであるパーセントインピーダンス法を交えて解説をしました。パーセントインピーダンス法は意味をしっかりと理解していれば非常に利便性の高い手法です。確実な電気保安を実現することも電気技術者の大切な責務です。そのために複雑な計算を回避して現実的な道を辿るのもありだと考えます。
配線が簡単に損傷しないため、また保護機器が確実にはたらくためなどその他細部に目を配ることができるように知識を蓄えることはとても大切です。
これまで知り得た知識にこの知識も加えてより確実な電気保安に役立ててください。






