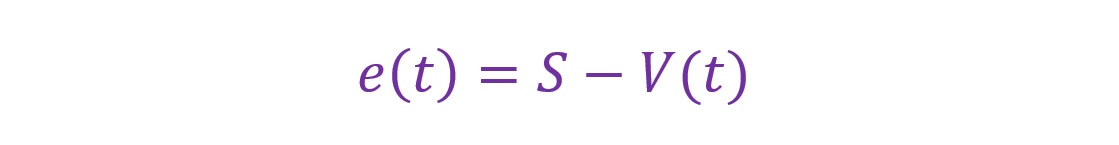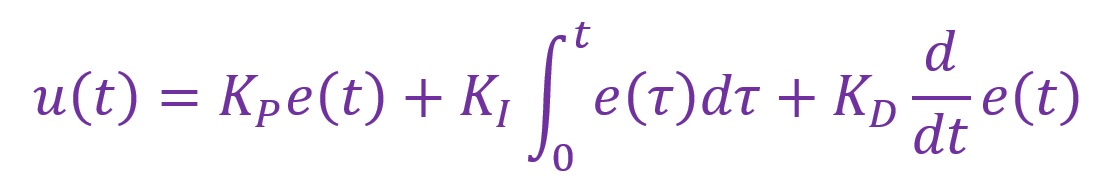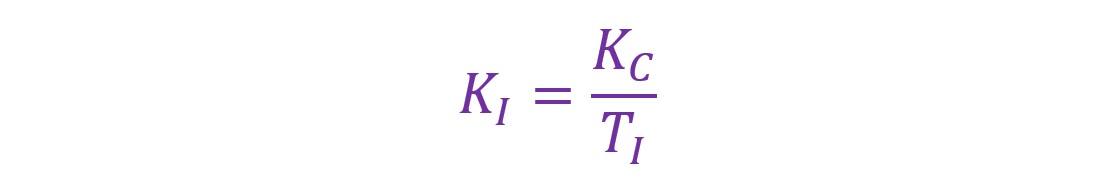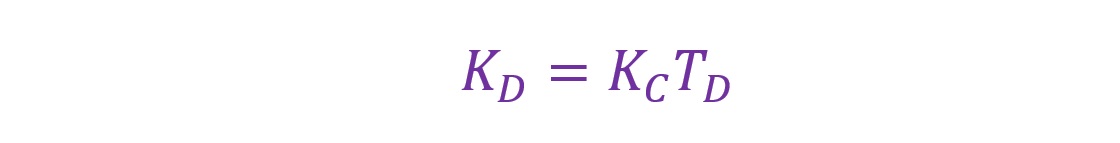1.ちょうどいい制御が目的
温度や流量その他圧力や電動機を制御するときどのようなプロセスの制御を用いて目的を達成するのが良いのでしょうか。
設計者側からみて最も簡単なのはON/OFF制御でしょう。しかしそうはいかない場合、つまりON/OFF制御では目的を達成できないケースは数多く存在します。
1)ON/OFF制御でもよい場合
まず、ON/OFF制御でも全く問題がないケースとはどのようなものなのでしょうか。温度制御を例にみてみます。
温度をコントロールするにあたって、ON/OFF制御でも良いケースというのは『A[℃]以上を保てば良い』や『B[℃]以下を保てば良い』などです。『100[℃]以上を保つ』制御ならば例えばですが、105[℃]で加熱制御を停止し102[℃]以下で再開するようなサイクルでONとOFFを繰り返すようにすれば目的を達成できそうです。熱伝導率や熱媒の温度、または加熱対象の量などで加熱の停止温度や再加熱温度は変動するかもしれませんが、条件自体に余裕がありますので設定の合わせ込みもそう難しくはありません。
これ以外でも、例えば『150±10[℃]を保つ』制御であったとしても許容の幅が広いのでON/OFF制御で充分対応可能ではないかと予測できます。もちろん先の熱伝導率等の条件にも左右はされますが、よほど少量のものや熱伝導率の高いものでなければ問題ないでしょう。
ただし、ON/OFF制御の場合は必ずといっていいほどハンチングという設定値に対するオーバーシュート(行き過ぎ)とアンダーシュート(戻り過ぎ)を繰り返すこととなり、制御対象は振動することとなります。それもそのはず、ONとOFFを繰り返すこと自体が繰り返し動作となりますので対象の制御結果が振動するというのはごく自然なことです。
そしてこの振動現象は高精度な制御を必要とする系では致命的な欠陥となります。またエネルギー使用の合理化の観点からも不利といわざるを得ません。
2)ON/OFF制御よりも精度よく素早く
ON/OFF制御ではハンチングという振動現象を抑制できないということはわかりました。ですが、もっと高精度に制御する方法は無いのでしょうか。例えば温度制御において、せめて±1[℃]に収めたい場合やもっと高精度に制御したい場合などの手法というのは実現不可能なのでしょうか。
いえ、そんなことはありません。すでに確立している制御の手法に「PID制御」というものがあります。PID制御は「フィードバック制御」のひとつというより既に代名詞といっても過言ではない制御手法となります。これは先のON/OFF制御の大きなデメリットとなる振動現象を抑制しつつ速やかに目標に到達させるということを目的とした制御方法です。「フィードバック」というくらいですので、制御対象の数値情報を演算器に戻し、そこから目標値と得た実測値の偏差を割り出して操作量を決定します。
応用幅は広く、先に挙げた温度や流量の制御はもちろんステアリングの制御やインバータとの連携による回転数を制御することによる圧力などの制御等に用いることも可能です。設定を工夫することで追従制御としての応用も可能です。
ここからは、この「PID制御」がどのような手順を踏んでどのような結果をもたらすのかについて説明します。
2.PID制御は制御動作の組み合わせ
では、具体的にPID制御がどのようにして制御対象を目標に到達させるのかについてみていきます。
この制御では3種類の計算が実行されて最終的な操作量となっています。その3種類は以下のものとなります。
①比例制御(P制御)
②積分制御(I制御)
③微分制御(D制御)
①〜③は各々、「proportional(比例)」「integral(積分)」「differential(微分)またはderivative(導関数)」でこれらの頭文字をとってPID制御です。
1)偏差
PID制御はフィードバック制御ですので、常に実測値を取得(フィードバック)し目標値と照らし合わせてその差異を割り出したうえでアクションします。
ですので、最初に行われるのは目標値と実測値の引き算です。この引き算の結果が後の比例制御,積分制御,微分制御に影響してきます。
なお、この偏差は数値記号としてよく「e」と表され、その関数は時間と共に変動することから「e(t)」と表現されることが多いです。
上の式では目標値を「S」とし、実測値を「V」としています。式の意味するところは「目標値に対するある時間における実測値の差異を偏差とする」という意味です。
2)比例制御(P制御)
比例制御の作用について説明します。
比例制御の目的とするところはいち早く目標値に近づけるということと振動の抑制にあります。偏差に対して素直に偏差の分だけを操作量とするよりも、そこに係数をかけることで偏差の倍数として操作量を決定します。そうすることで実測値の目標値への接近が早くなります。
式で表すと以下のようになります。操作量を「u」としています。
このときの「KP」を比例ゲインといいます。
比例制御により目標値(付近)にいち早く近づきかつ振動の抑制は可能となりました。しかし、この比例制御には致命的な欠陥があります。それは「目標値からズレた状態で安定してしまう(オフセット)」ということと、「短期的ではあるものの大きなオーバーシュートとアンダーシュートが発生する」ことです。これらは必ず解消すべき欠陥です。
3)積分制御(I制御)の追加(PI制御)
比例制御の欠陥のひとつであるオフセットを抑制するための制御方法がこの積分制御という方法です。
比例制御によって発生したオフセットと目標値の偏差を定められた時間で積分して得られた操作量を比例制御で得られた操作量に加算することでオフセットの解消をねらいます。
比例制御に積分制御が加わるのでPI制御といわれる制御方法となります。
計算式は以下のとおりです。比例制御に積分制御を加えていることがわかります。このときの「KI」を積分ゲインといいます。計算式に「τ」という記号が出てきていますがこれは「タウ」とよみます。定積分の積分範囲ですでに「t」が使用されていますので混乱を避けるためにこの記号を使用していますが、同じ時間を表現するτに置き換えているだけであると考えてください。
この方法は偏差に伴った計算値を加算することとなりますので、オフセット数値を単純に加算するより目的に沿ったものとなりまた時々刻々変化する偏差にも対応できます。
ここで注視すべきは先ほどの比例制御のときよりハンチングが大きくなってしまっているということです。当然と言えば当然なのですが、比例制御によって発生したオフセットを解消するために制御量を追加していますのでその影響がハンチングの増加傾向という形で発生してしまったということになります。これではオフセットがなくなったとはいえ理想的な制御とは言い難いです。
次の項ではこのハンチングを解消するための制御動作について説明します。
4)微分制御(D制御)の追加(PID制御)
比例制御で発生し積分制御の追加であろうことか増加傾向になってしまったハンチングについて改善するための制御が微分制御となります。偏差の変化を微分してこれまでのPI制御で算出された制御量に足し合わせます。
以下はPI制御に微分制御を足し合わせたPID制御の計算式です。「KD」を微分ゲインといいます。
これでPID制御における制御上の計算式が完成したことになります。ここまで説明した三つの動作の和を最終的な制御量として出力することで目標値にいち早く近づきかつピタッと落ち着く制御が可能になりました。外部の機器を動作させる場合はもちろん制御量を電気信号に変換する必要があります。ですのでここから先は信号変換という別の作業となります。
グラフイメージは以下になります。各ゲインの調整にもよりますが下のイメージのような制御を実現することも難しくありません。うまく調整できればもっと理想的な制御も可能です。
ここで「あれ?」となる人も多いのではないでしょうか。ハンチング抑制のための微分制御ということですが計算式では微分制御も加算されていることに違和感を覚えたのではないでしょうか。もし本当にただ単純な加算であればハンチングはさらに増加傾向になってしまうのではないかという疑問です。
このような疑問に回答します。
PID制御は三つの制御動作においてどれも「偏差」に対しての挙動となります。制御の目的はこの偏差を「0」にするというところにあります。ということは、偏差は時間が経つにつれ減少していくはずです。いや、減少させなければいけません。これが大前提です。
微分の数学的な目的は関数のある時間における傾き(接線)の割り出しにあります。これを合わせて考えると、時間と共に減少していく数値(差)の傾きを算出するということになります。
つまり、右肩下がりになる関数の傾きを算出して加算するということです。これは結果的にマイナスの値を加算することになります。こうして微分制御は抑制動作としてはたらきかけることとなるのです。
とはいえ、オーバーシュートのときを考えると「偏差は増えていくんじゃないの?」という疑問も湧きますね。そのとおりです。
今まさにオーバーシュートしているという場合はそもそもの偏差の式「e(t)」がマイナスの値として算出されます。ということは比例制御と積分制御がマイナスで算出され制御量を減らす方向つまり「0[%]方向」に働きます。同時に微分制御もマイナス方向に偏差が増加しますので制御量を減らす方向へ働きます。しかし、実測値が頭打ちして再び目標値へ近づきはじめたら比例制御と積分制御が依然、制御量減少方向へ働いていても微分制御だけはいち早く制御量を減らし過ぎないように抑制する働きに変わります。
このようにしてPID制御は「素早く目標値に近づくように」かつ「オフセットが発生しないように」そして「ハンチングをしないように」バランスをとりながら操作量を算出決定します。
3.調節計の実際
ここまでPID制御の概要と理論について説明をしてきましたが、調節計でPID制御を使用して何かしらの機器を動作させた経験のあるひとならば以下のような疑問をもつかもせれません。
「『比例ゲイン』『積分ゲイン』『微分ゲイン』なんて項目を変更したことはないぞ…代わりに『比例帯』『積分時間』『微分時間』なら触ったことがあるけど。」
そうなのです。PID制御の理論はこれまでの説明でよいのですが、実際の調節計では上記のPID制御の式を変形して利用しています。このことについて簡単ですが触れておきます。
1)調節計でのPID制御の式
いきなりですが調節計で使用されている式を以下に記載します。
上式の「MV」は制御量です。そして「KC」は比例帯、「TI」は積分時間、そして「TD」は微分時間という係数になります。調節計でのPID制御ではこの三つの項目を変更することで最適な制御を実現します。
以降でなにをどのように変更したら上記の式になるのかを説明します。
2)PID制御の式の変形について
上記は既出のPID制御の式です。この式に対して以下の式を各々代入し、くくりだす(因数分解する)ことで先の「MV=…」の式が導出されます。
3)動きへの影響
調節計内部での演算式について説明をしましたが、では具体的な動きとしての影響はどうなるのでしょうか。ひとつずつ簡単ですが説明します。
まず「KC」についてです。この値を大きくすると偏差に対する操作量が大きくなります。その結果ハンチングも大きくなります。オフセットは残りますが小さくなります。
続いて「TI」についてです。この値は小さくするとその影響が大きくなります。結果、オフセットはなくなりますがハンチングの振幅が大きくなりと抑制までの時間が長くなります。
そして、「TD」です。この値を大きくすると、その影響は大きくなります。これにより目標値への到達時間は伸びますがハンチングを抑制する影響も大きくなります。
4.オートチューニング
PID制御を実行するのにとても便利な、調節計の「オートチューニング」について説明します。
1)勝手に算出
ここまで説明したPID制御の各係数に関して全てを理解し都度計算してから決定していくには非常に手間がかかります。ですが、各調節計には必ずといっていいほどオートチューニングという機能があります。これは、実際にPIDによる制御を実行しながら最適な係数を自動計算で決定してくれるとても便利な機能です。
その操作方法は機器ごとに違いますのでこれに関しては取扱説明書をみてください。ほぼ必ず載っているはずです。
2)オートチューニングが終わらない!
オートチューニングは、たいていサンプリングと計算が完了すると各係数を自動で登録してそのまま制御を続行してくれます。
しかし、いつまで経ってもこのオートチューニングが完了しない場合があります。それが「目標値で安定してしまってから開始したチューニング」です。
偏差がほとんど無い状態でしかもそれ以降の変化も乏しい状態でチューニングを開始してしまうと偏差を元に計算するPID制御の情報が不足してしまい、結果いつまで経っても完了しないことになります。
各調節計にはPIDの初期値というものがあり、実績などからある程度常識的な値が登録されています。一度定常状態に入ってからチューニングを開始した場合、これまでどんなに時間がかかっていたとしてもそれはデータとしてとり上げられることは無くこれ以降の情報でしか演算できません。そうするといつまでもオートチューニングが終わらないことになってしまうおそれがあります。
オートチューニングは必ず制御開始と共に始めるようにしましょう。
5.負荷とのバランス
これまでの説明で「なんだかPID制御って賢い」というイメージが湧いてしまいます。しかし、そうではありません。
少しの操作で大きすぎる変化をしてしまうものには追従が非常に難しくなります。また、操作量100[%]でも目標値まで到達できない能力の機器の場合は制御不可能となります。
当然のことながらではありますが、負荷に対してちょうどいい出力をもつ機器の選定が必須であるということです。