1.三平方の定理と三角関数
電気を理解しようとしたとき、多くの場面で数学における知識を求められることがあります。そして電気に関する理解を深めようとすればするほどにこの数学の壁が立ち塞がります。
そのような切っても切り離せない数学の中でも、今回は「三平方の定理(ピタゴラスの定理)」と「三角関数」について説明します。これらは、電気を扱う中でも「交流回路」を理解するうえでの必須知識となります。
三平方の定理を理解せぬままでは交流回路計算の初歩的な段階でつまづくこととなります。実務上でも悩まされることが想像に難くありません。
そして、三角関数も同様です。そもそも交流回路(電源)には時間と共に極性が入れ替わるという特徴があり、電圧や電流の時間的変化が「正弦波」という形のグラフで表されます。そのため交流回路での電圧や電流の瞬時値(ある瞬間の値)を知ろうとする場合、必ず三角関数の概念を必要とします。また、交流回路では「位相」や「力率」という考え方が必要になりますが、ここでもことごとく三角関数が絡んできます。さらに、「電動機を動作させるためにはどれくらいの電力を供給すべきか」や「電力有効利用のためのコンデンサ容量計算」など、この他にも様々な場面で三角関数の理解を求められます。電気を扱うのであれば是非とも手に入れておきたい知識になります。
2.三平方の定理(ピタゴラスの定理)
ここで説明する「三平方の定理」は別名「ピタゴラスの定理」ともいわれ、このあとの「三角関数」へ進むための大切なステップとなります。三平方の定理を理解せずに三角関数のみを理解しようとしても、単純に計算できなかったり、得られた値を目的に合わせて利用できなかったりと非常に不便この上ない状態に陥るのみです。
焦ることなく大切なこのステップから理解していきましょう。
1)c2=a2+b2
見出しの式「c2=a2+b2」が三平方の定理の全てです。もうここでの結論が出てしまいました。ですが、これでおしまいというにはあまりにも説明不足なので、もう少し話を進めます。
先ず、三平方の定理は大前提として「直角三角形」について述べています。このことを見落としたまま先へ進むと迷宮へまっしぐらとなるだけですのでこの約束を失念しないように気をつけてください。
大切なことなのでもう一度言います。
「三平方の定理は直角三角形が前提」です。
この前提を踏まえたうえで、先ほど出てきた式が何を表しているのか説明します。
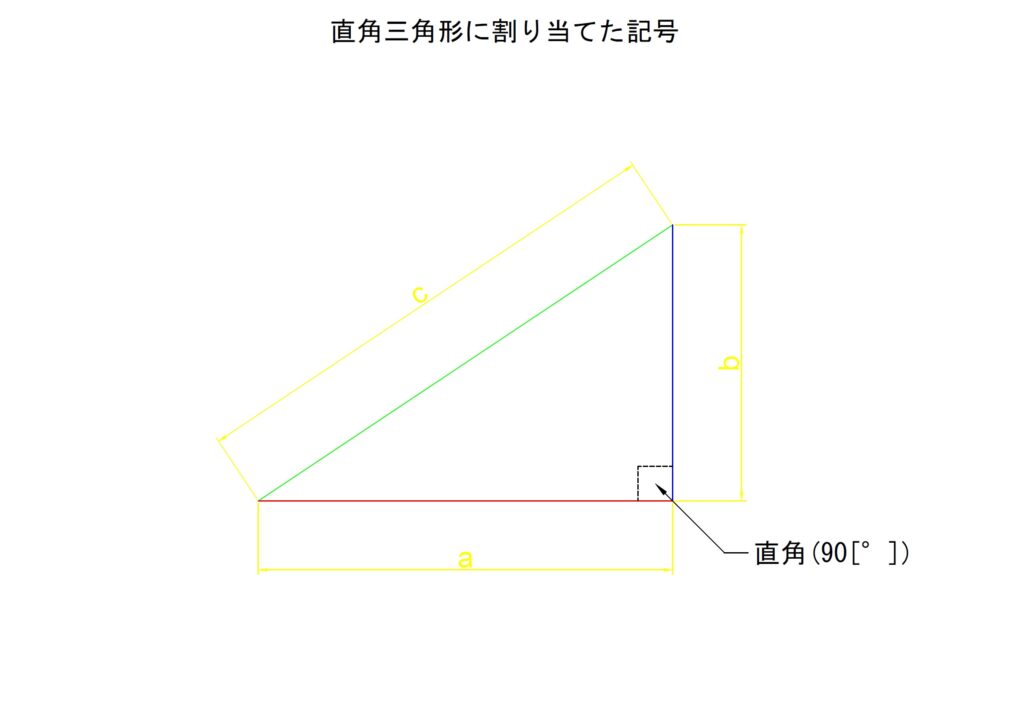
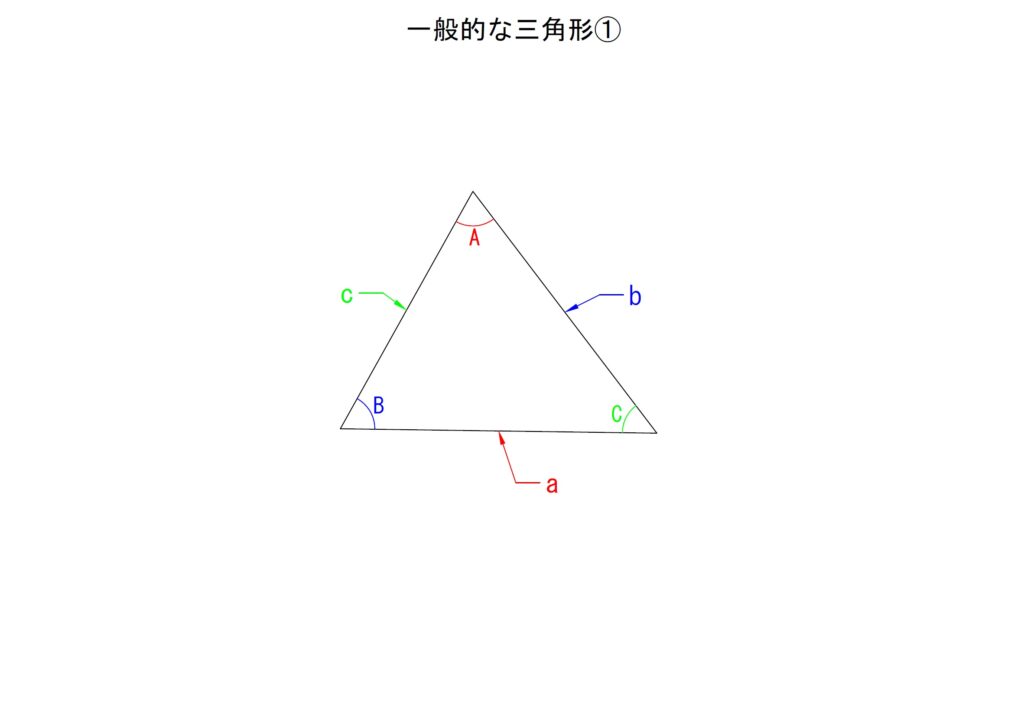
以下の図をみてください。単純な直角三角形です。ただ、この三角形の各辺には各々「a」「b」「c」と記号が割り当てられており、これらは同時に長さも表すこととなります。これでピンとくる人もいるでしょう。
先ほどの式にあった「a」「b」「c」はそのまま図の各辺「a」「b」「c」に対応します。
つまり「c2=a2+b2」では、最も長い辺を2乗したものは残りの辺を各々2乗して足し合わせた値と等しいことを表しています。
2)各辺の名称
各辺には名称があります。
三平方の定理における演算時に部位を取り違えないようにしたり、この後に出てくる三角関数で部位を取り違えたりしないようにするためには、なるべく短い文字でどの辺のことを指すのかを特定できる方が便利であり、より確実です。
①基準になる角
先に、各辺には名称があると述べましたが、三角形を含む様々な図形は視点がどこにあるかで特定するものが変わってしまいます。ですので誰がみても統一できるようにする必要があります。
三角形はその名のとおり三つの角から形成され、結果三つの辺を有する単純な図形になります。
このような単純な図形であっても、数学で用いる場合は角度や辺の長さを数値で正確に知る必要があります。そして割り出された数値が何を表すのかも短時間で正確に伝わるようにする必要があります。先程述べたように、間違いや見た人の解釈によって取り違えることがあってはいけません。
三平方の定理や三角関数など数学的に用いる直角三角形には各辺に名称がつけられています。これにより、説明や証明でどこのことを指しているのか特定できるようにしています。そしてそのためには基準となる何かが必要となります。そしてこの基準となるのが「ある角」となります。
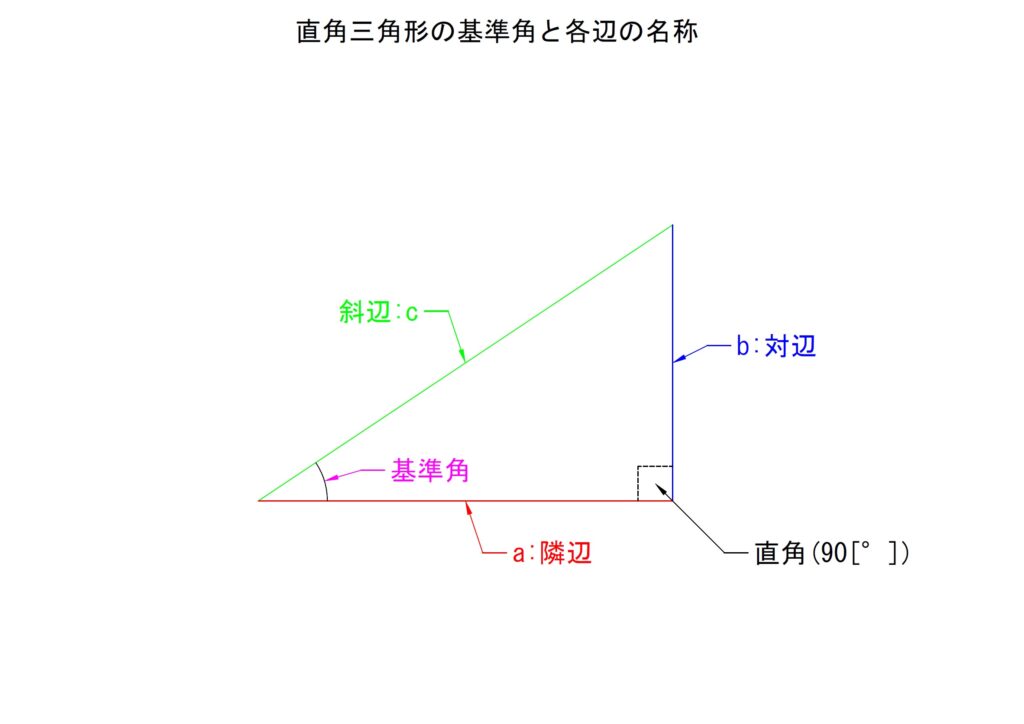
この記事内では基準となる「ある角」を「基準角」とします。
三平方の定理で用いる直角三角形において、基準角は直角以外の角のいずれか一つと定めます。
はじめのうちは、基準角を常に左側にもっていき、その反対側に直角をもってくる形で慣れてください。理由は、多くの説明でこの位置が採用される為です。
②辺の名称
基準の角が定まったら各辺の名称が決定されます。以下の図をみてください。
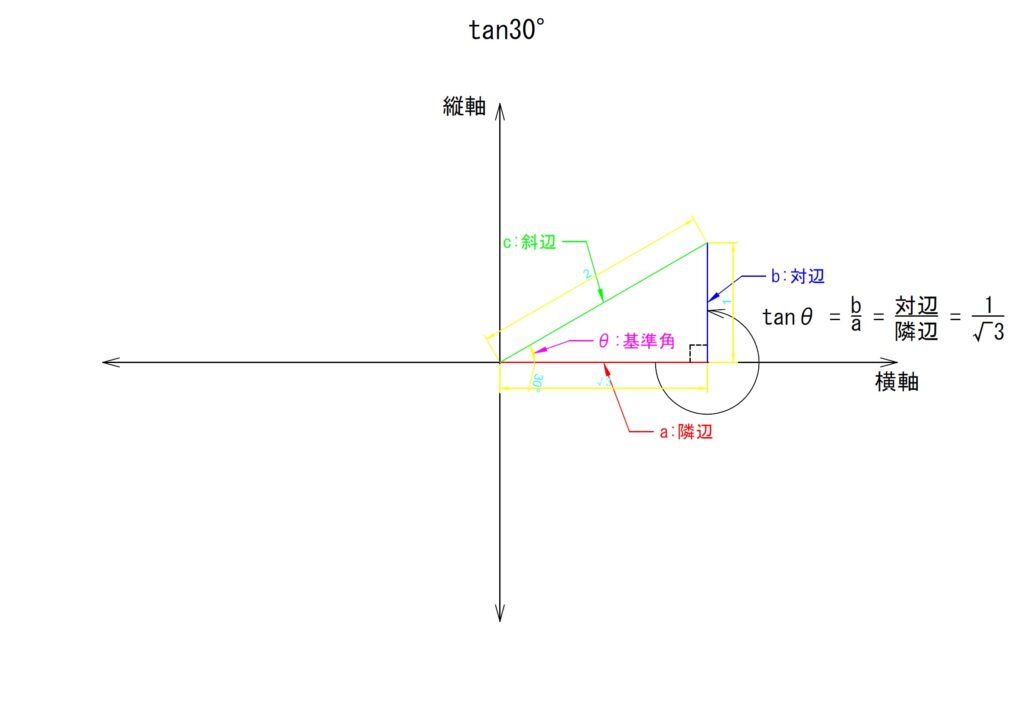
基準角から斜めに立ち上がる直線を「斜辺」といいます。そのままです。基準角から直角三角形の直角に向かう直線を「隣辺」といいます。基準角に対して向かい合う位置にある辺を「対辺」といいます。このように固定された名称を割付けることで記号より確実な特定を可能とします。
③「c2=a2+b2」の実際
基準角と各辺の名称を明確にしたところで、三平方の定理の実際をみてみます。2~3例あげて本当に式(c2=a2+b2)が成立するのか試してみます。
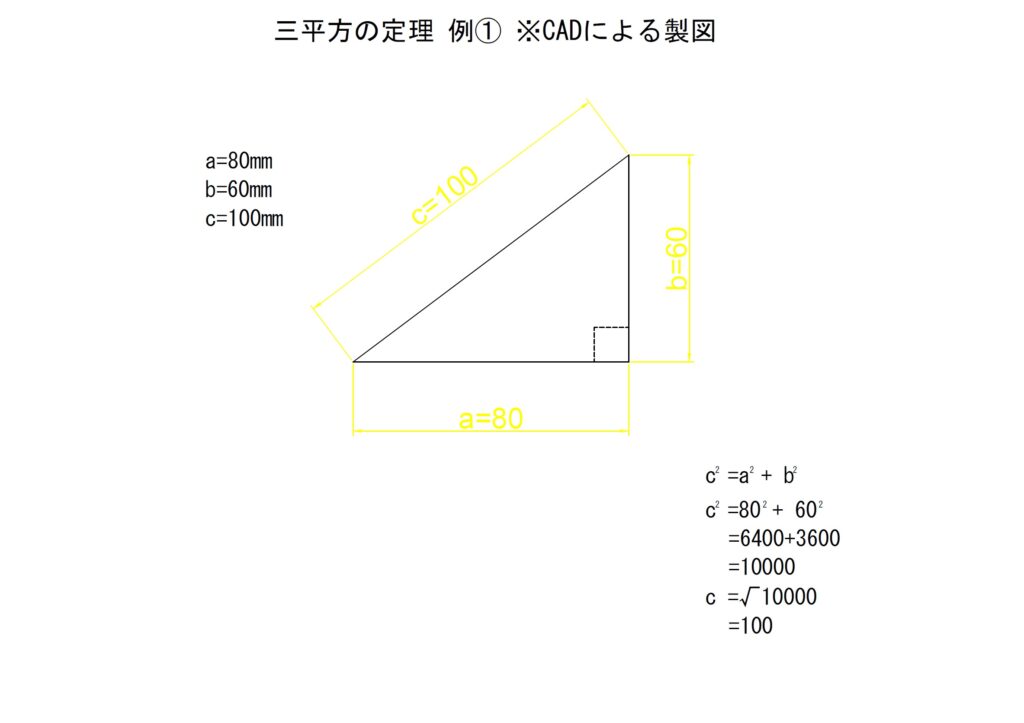
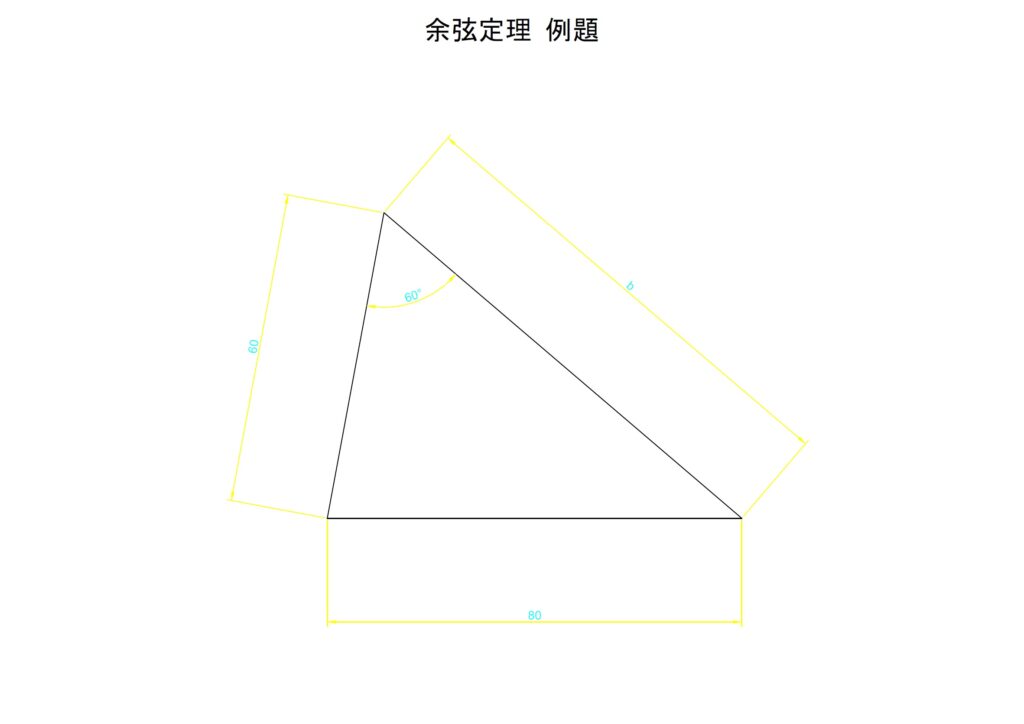
例① a=80,b=60
例の一つ目では隣辺aを80[mm],対辺bを60[mm]として斜辺cを算出します。以下に計算結果を記載します。
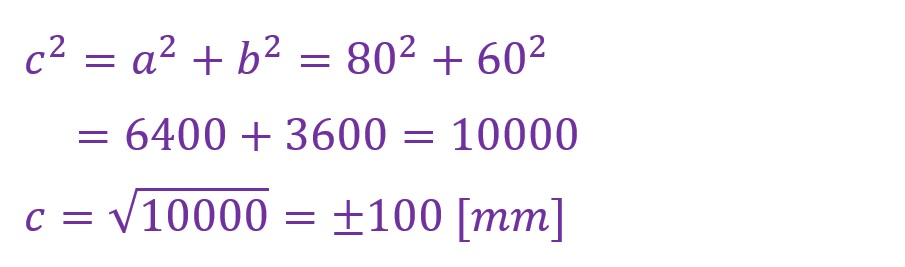
以下にCADで描いた直角三角形の寸法を記載します。きっちり斜辺が「100[mm]」になっていることがわかります。なお、負の数は逆方向の直線を形成するので考慮には含みません。
なお、この計算が合っているかどうかはセオリーのとおりに逆算(確かめ算)で確認できます。例えば対辺を逆算してみます。この結果が60[mm]になれば良いということです。
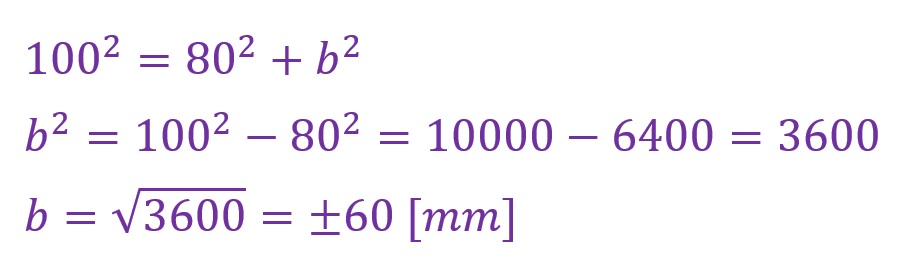
ねらったとおりに「60[mm]」が算出されました。これは隣辺で確認しても成立します。
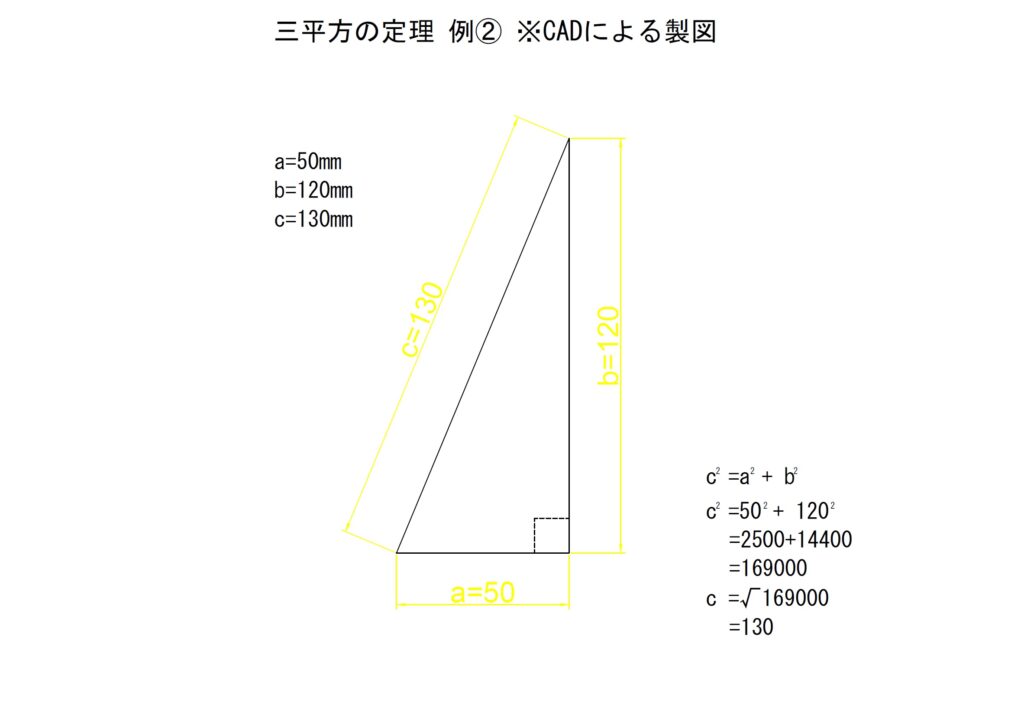
例② a=50,b=120
例の二つ目では隣辺aを50[mm],対辺bを120[mm]として斜辺cを算出します。以下に計算結果を記載します。
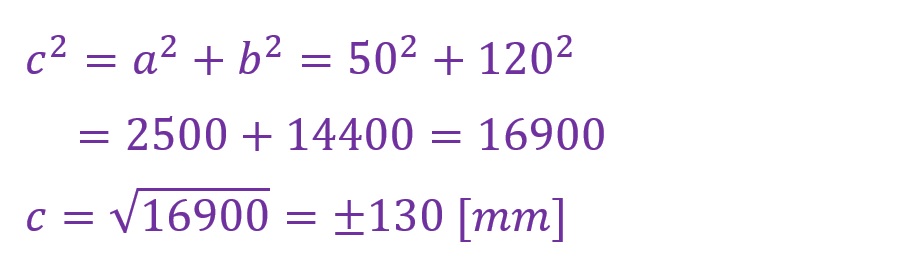
以下にCADで描いた直角三角形の寸法を記載します。斜辺が計算したとおりに「130[mm]」になっていることがわかります。負の数に関しては例①と同様です。
逆算で確認してみます。対辺を逆算します。この結果が120[mm]になれば良いということです。
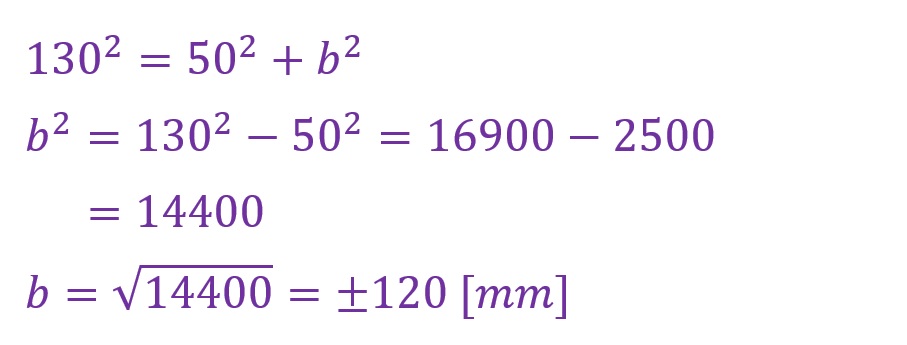
ねらったとおりに「120[mm]」が算出されました。
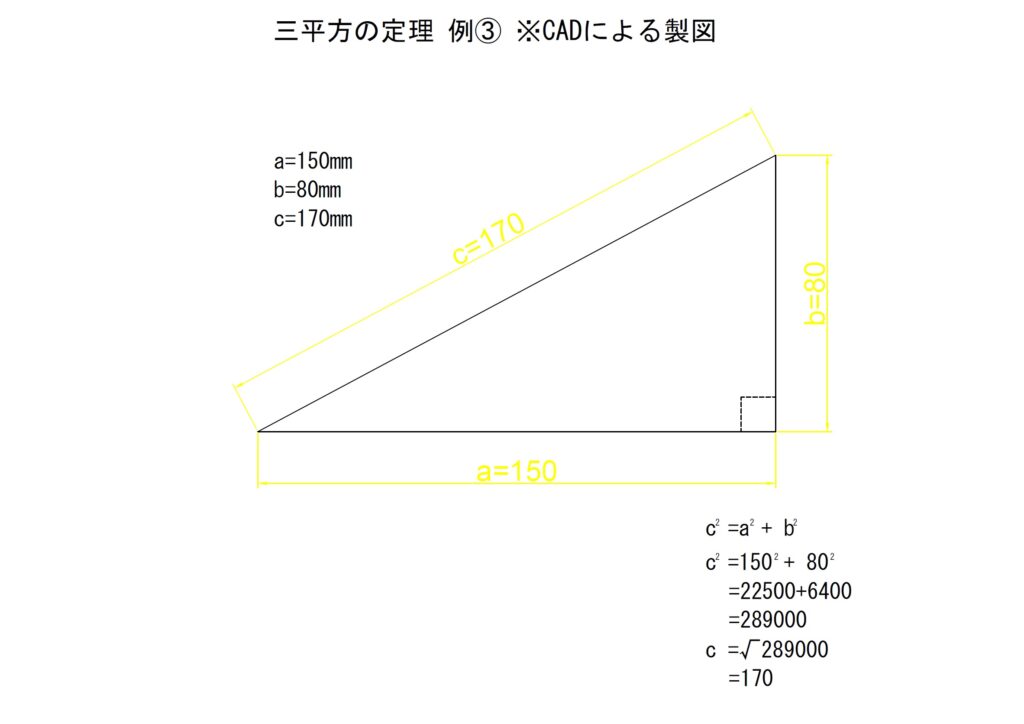
例③ a=150,b=80
例の二つ目では隣辺aを150[mm],対辺bを80[mm]として斜辺cを算出します。以下に計算結果を記載します。
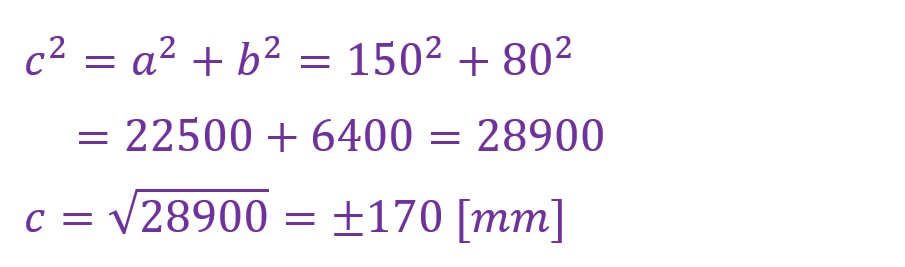
以下にCADで描いた直角三角形の寸法を記載します。斜辺が計算したとおりに「170[mm]」になっていることがわかります。負の数に関しては例①と同様です。
逆算で確認してみます。対辺を逆算します。この結果が80[mm]になれば良いということです。
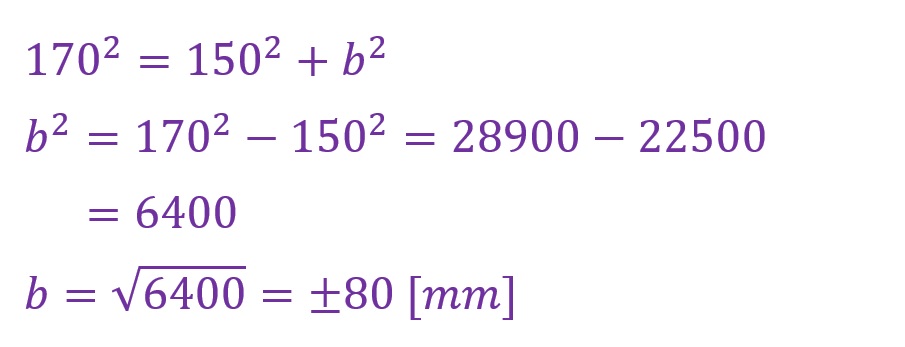
ねらったとおりに「80[mm]」が算出されました。
3)三平方の定理の証明
先の例から、如何なる直角三角形においても「c2=a2+b2」がおそらく成立しそうであるこということがわかります。
ここでは三平方の定理がなぜ成立するのかについての証明を試みます。
比較的わかりやすく有名な方法を用います。
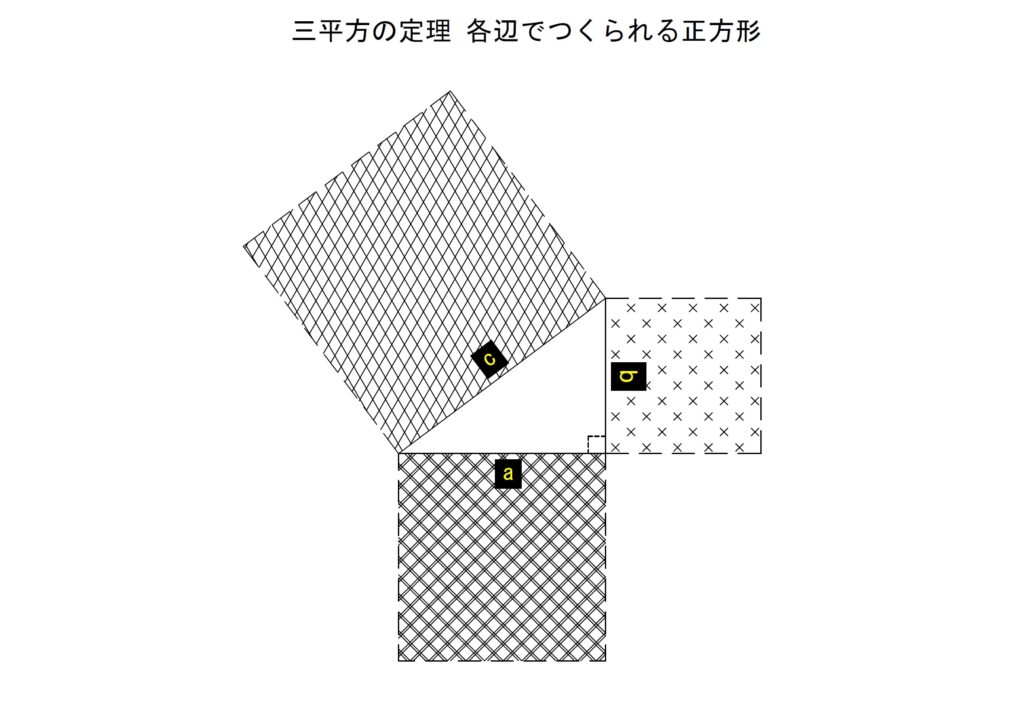
先ず「a2」「b2」「c2」は各々正方形の面積を表すと理解してください。この考え方が証明の理解を促します。
三平方の定理が述べているのは、斜辺cにより形成される正方形の面積が、隣辺aと対辺bにより各々形成される正方形の面積を足し合わせたものと等しいということです。
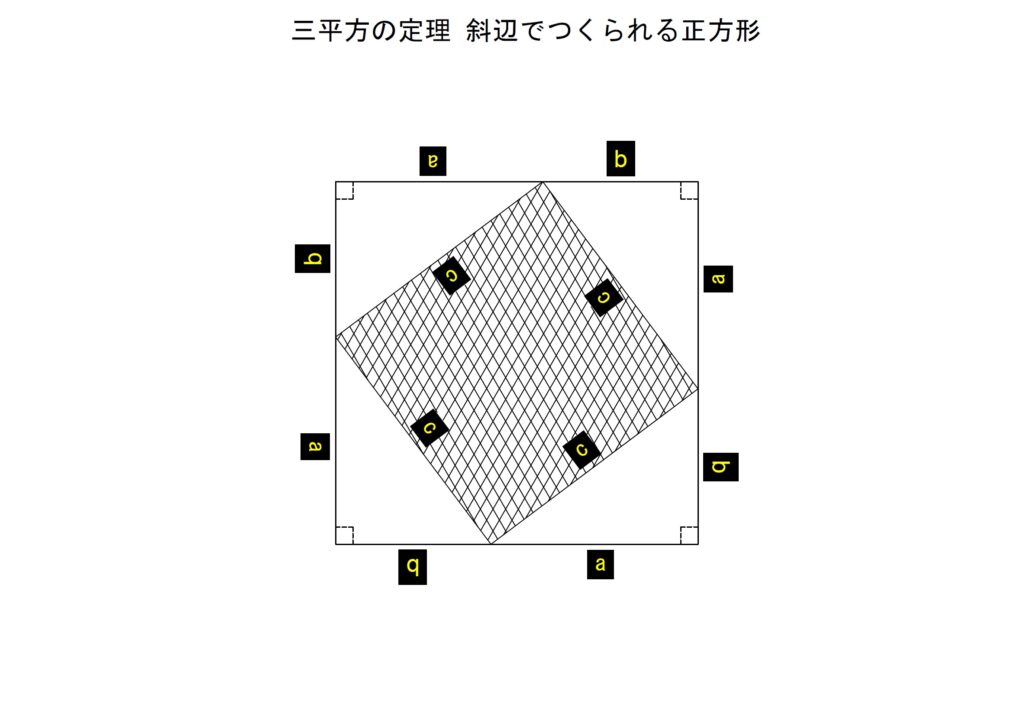
上の図の斜辺cで形成される正方形のみに着目した場合、以下の図のように表現することができます。
上の図では、内側に斜辺cにより形成された正方形と、外側に隣辺a+対辺bにより形成された正方形ができることとなります。
このことから外側の正方形の面積から周辺四つの直角三角形の面積を差し引き(減算)したときに内側にある斜辺cで形成される正方形の面積が得られます。その結果が「a2+b2」であればこの定理は成立するということになります。以下がその証明の式となります。直角三角形一つ分の面積を「Sd」とし、隣辺a+対辺bにより形成される外側の正方形の面積を「Ss」とします。更に、「Ss」から四つ分の「Sd」を差し引いた面積、つまり斜辺cでつくられる正方形の面積を「Sc」とします。
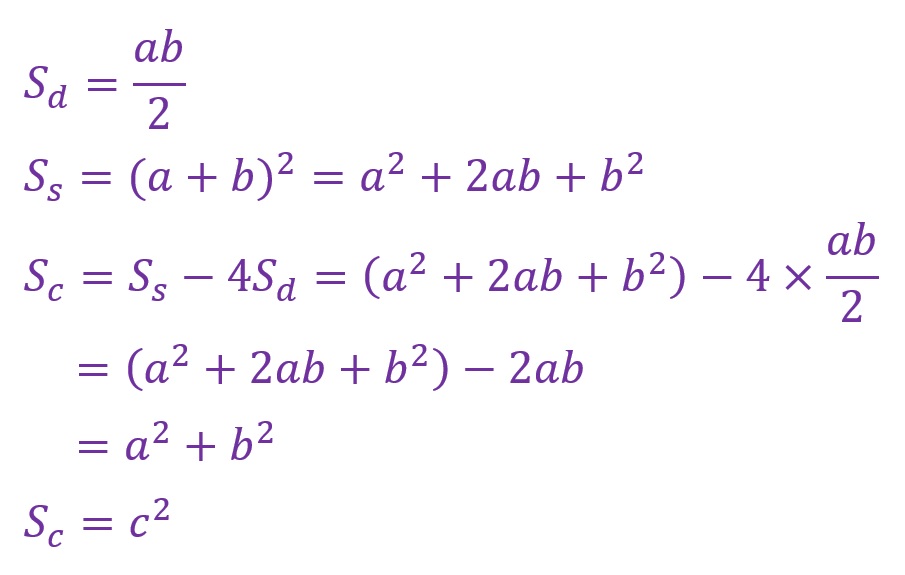
「Sc=a2+b2」が算出されたことにより、三平方の定理が証明されました。(式中の括弧はわかりやすさのために付加したのみです。)
三平方の定理の証明はいくつかの手法があるようですが、今回はそのうちのおそらく最もわかりやすく、かつ有名な一つを説明しました。
3.三角関数
三平方の定理をしっかり理解できたならば次は三角関数へのステップアップとなります。
三角関数を理解することにより、交流回路で電圧や電流がどのように変化しているのかを把握したり、供給された電力がどれくらい有効利用されているかについて算出することが可能になります。
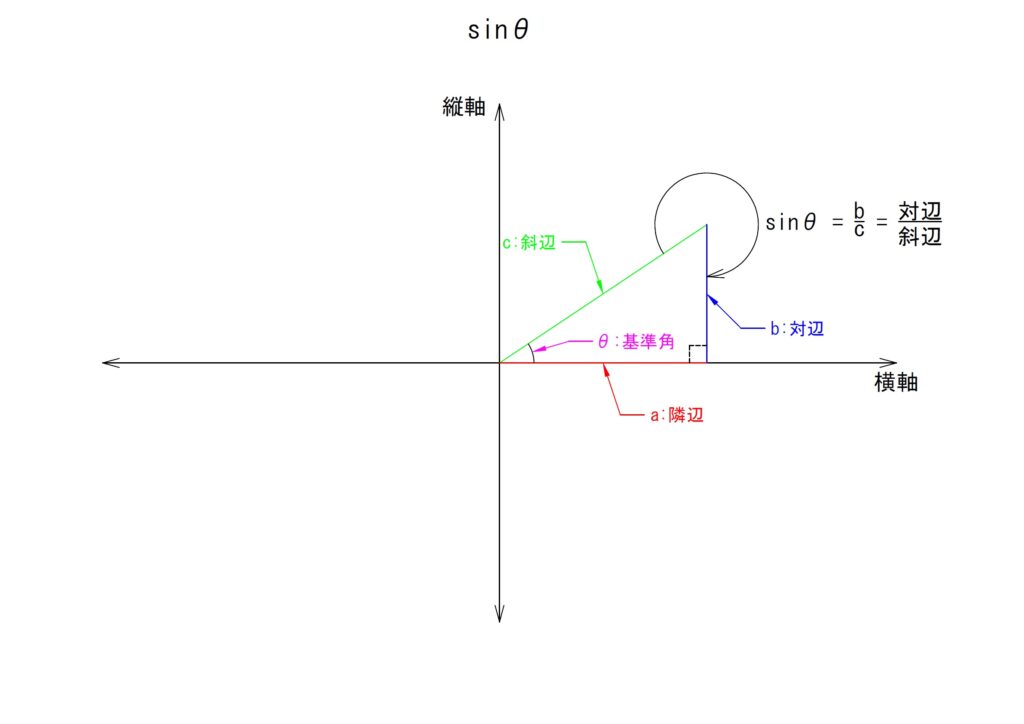
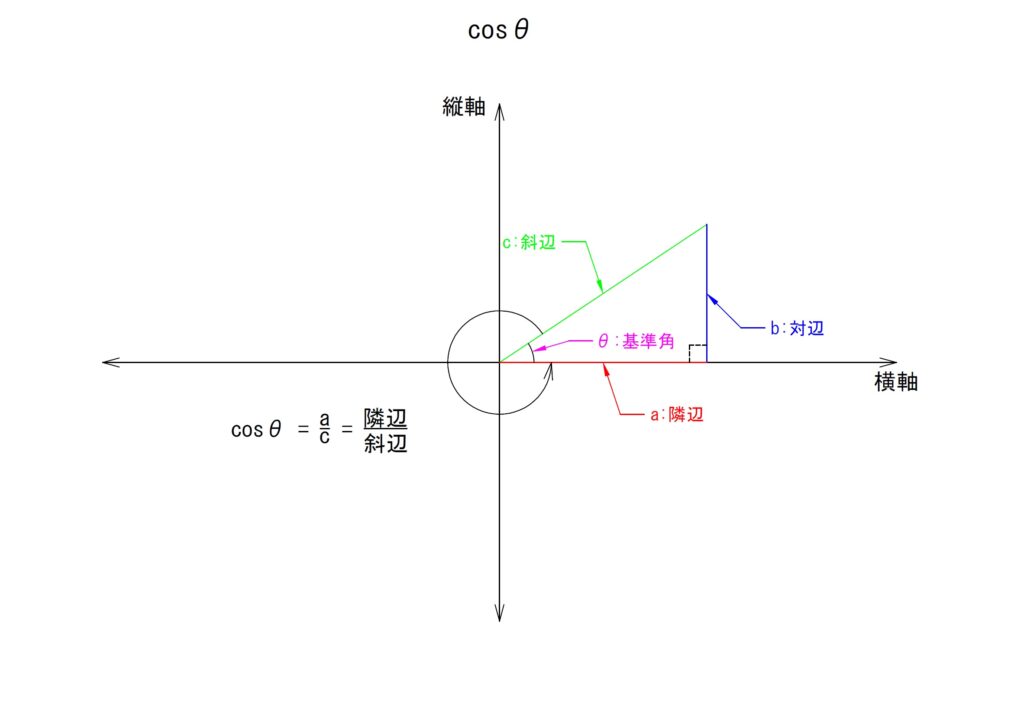
1)ここでも直角三角形を使う
三角関数においても、基本的には三平方の定理と同様に直角三角形を前提とした説明になります。例外的なテクニックはあるものの原則は直角三角形での説明あることを失念しないように気をつけてください。
また、三平方の定理の項で説明済みの各辺の名称は三角関数でこそ必要になってきます。どの辺を何と呼称するかをしっかりとおさえておいてください。
2)基準角と平面
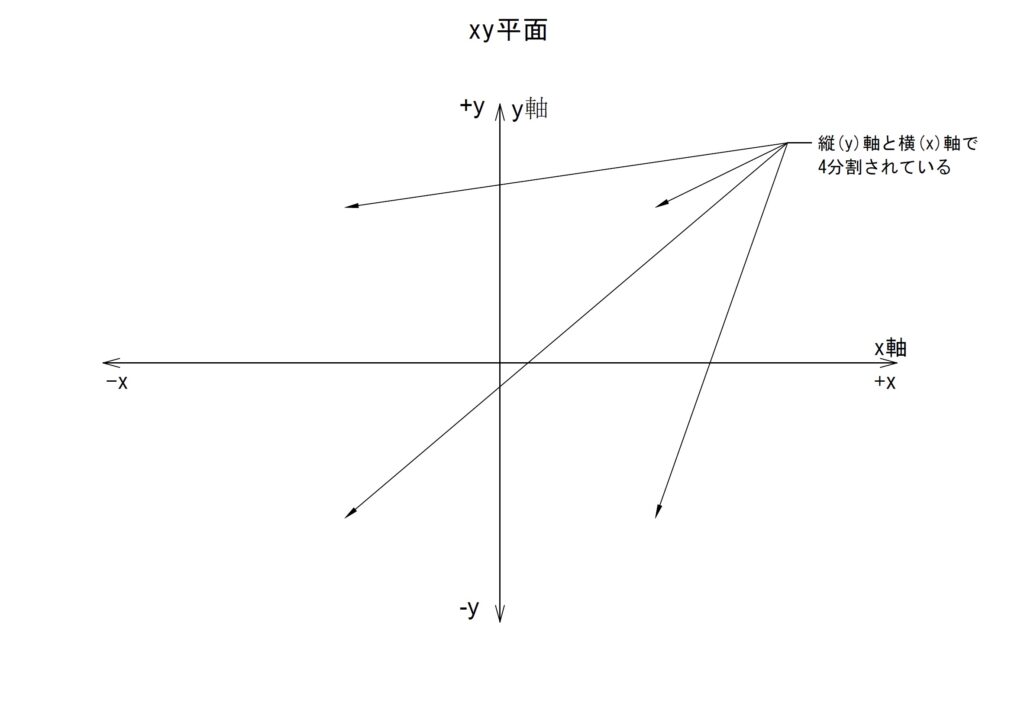
三角関数は他の関数同様に2軸の平面上での話となります。2軸は各々縦軸と横軸になります。一般的には縦軸を「y軸」とし、横軸を「x軸」とします。このことからこの平面を「xy平面」とよぶことがあります。
軸への記号割り付けについては、基本的には任意であり、必要に応じて関数や値の意味を表しやすいものを割り付ける場合もあります。
また、xy平面における各軸(x軸,y軸)が交わる一点を「原点」といいます。原点は数値でいうところの「x=0,y=0」のポイントとなります。座標として表現すると、「(x,y)=(0,0)」となります。
平面の構成や原点に関しては三角関数以外の関数やグラフにおいても共通です。
xy平面に関しては、このような概念があることを充分に理解してもらえれば大丈夫です。ここで大切なことは縦(y)軸と横(x)軸に正負の概念があることと平面が軸で4分割されているということです。これは後述の「象限」の項で必要となってきます。
3)各辺の比
三角関数は各辺の比率を表します。これが三角関数の主旨となります。基準角がある角度にある場合の各辺の比を表現したものが三角関数となります。
三角形を形成する直線は三つあり、そのうちの二つを取り出してその比を計算します。ですので、三角関数では基本的に六つの比が得られることとなります。六つの比は以下のとおりとなります。






特に「イ」〜「ハ」が頻出の比であり、「イ」を「サイン」、「ロ」を「コサイン」、「ハ」を「タンジェント」といいます。また、記号で「サイン」を「sin」、「コサイン」を「cos」、「タンジェント」を「tan」と書き表します。
上記には日本語での名称もあり、「sin」で表されるものを「正弦」,「cos」で表されるものを「余弦」,「tan」で表されるものを「正接」といいます。
ただし、これらには必ず角度の概念を必要とします。そしてこのときの角度は基準角のものを指します。基準角としての角度が決まらないということは直角三角形が形成されていないということとなり、そこには比べる辺も存在しないということとなります。
つまり「sin」「cos」「tan」は、それらのみが単独で値を特定できるものではなく、角度の情報とともに成り立つということです。
例えば基準角を「θ」とすると各々「sinθ」「cosθ」「tanθ」という形になります。そしてこれらは基準角が「θ°」のときに形成される直角三角形における各辺の比として決定される値になります。以下の図にて「θ=30°」のときの各値を記載します。



なお、「ニ」〜「ヘ」は「イ」〜「ハ」の逆数と考えて差し支えはありませんが、一部「0」が関わる場合は注意が必要です。(例えば「cosec90°」など)。
「ニ」を「コセカント」、「ホ」を「セカント」、「ヘ」を「コタンジェント」といいます。また、記号で「コセカント」を「cosec(csc)」、「セカント」を「sec」、「コタンジェント」を「cot」と書き表します。



4)弧度法
新しい単語が出てきました。「弧度法」というものですが、これは角度の表現方法の一つです。
通常、角度を扱う場合にその単位として「度」を用います。しかし、関数(特に三角関数)で角度を扱う場合、他の要素に対してその指標が違い過ぎるため同じ基準下で扱うことが難しくなります。例えば「長さ」に対して「角度」を割り出すなどです。そしてこのようなときに役立つのが弧度法という角度表現方法です。
①弧度法の定義
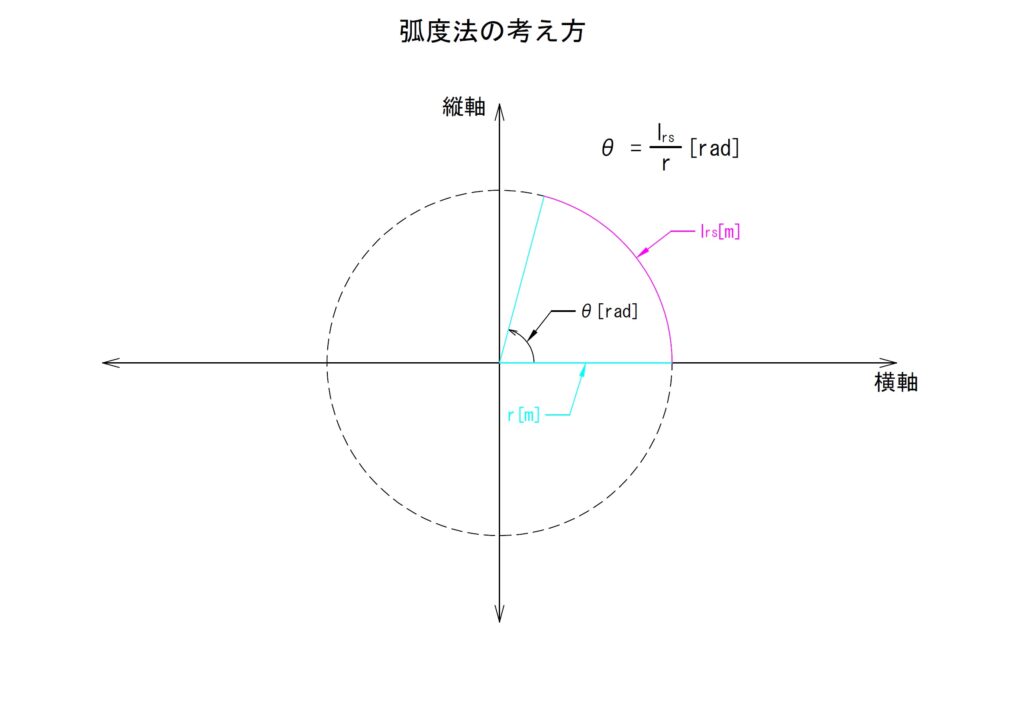
弧度法の定義は「扇形の半径と弧の長さが等しいとき、その角度を「1[rad]」とする」というものになります。言い換えると「扇形の半径を「1」とするとき弧の長さが「lrs」ならば、その角度を「lrs[rad]」とする」となります。
以下に定義式を記載します。ここでの弧度法による角度を「θr[rad]」とします。単位のよみは「ラジアン」です。
弧度法の定義式

弧度法で定義されていることを図で表すと以下のようになります。
上の図からもわかるとおり、弧度法によって、角度を「弧と半径の長さの比」で表現することができています。
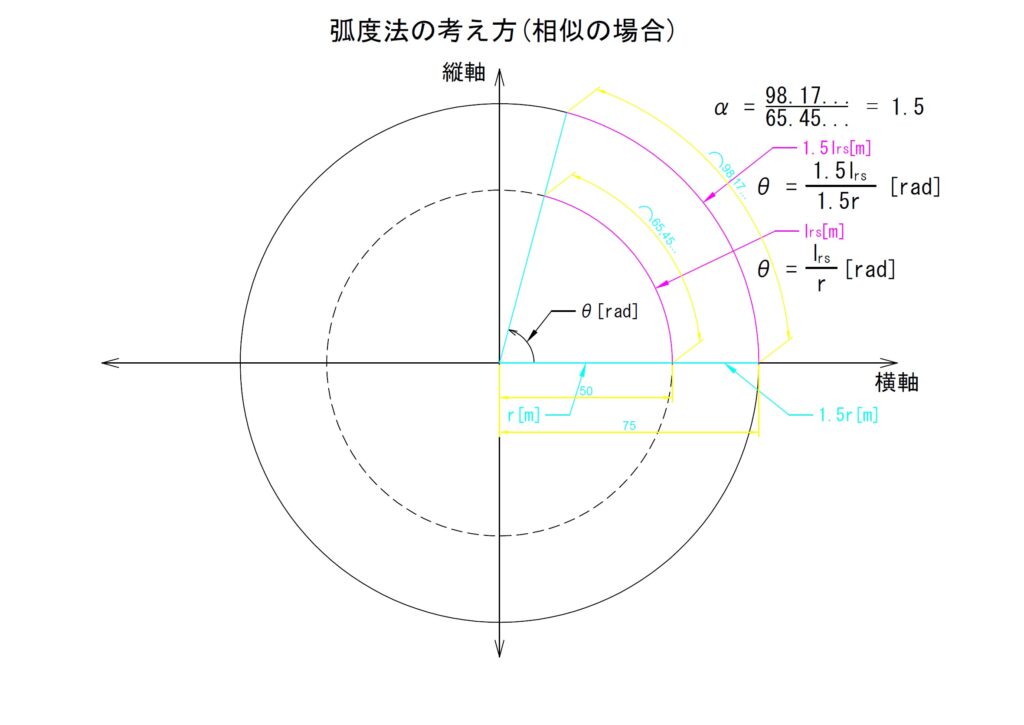
そしてこの「θr」は、あくまで半径と弧の比であり、半径の長さのみに直接影響をうける値ではないこと、つまり相似形の扇形でも「θr」の値に変化が無いということもわかります。それは弧度法が角度の表現として成立していることを意味します。
②単位円
上記から弧度法では「単位円」という考え方が多用されます。単位円というのは半径「r」を「1」とする考え方です。単位は「m」でも「cm」でも良いです。そのとき扱うスケールで構いません。
場合によっては任意の基準長を「1」としても良いです。ただしこの場合は任意の基準長を弧の長さにも適用する必要があります。
いずれにしても単位円を用いて「r=1」とすることで弧度法はよりわかりやすくなります。
つまり「r=1」のとき「lrs=1」ならば「θr=1[rad]」となり、「lrs=2」ならば「θr=2[rad]」となりさらに「lrs=3」ならば「θr=3[rad]」となります。
定義式に「r=1」を代入することで上記がよくわかります。



③弧度法と「π」
弧度法ではしばしば「π」という記号が出てきます。この「π」が弧度法をよりわかりにくくしているのではないでしょうか。
「π」はみなさん知ってのとおり「円周率」というものです。値としては通常「3.14」として学習します。また「率」なので単位はありません。
なぜ弧度法にはこの「π」の表現が多いのでしょうか。それには円周の長さの算出が関係します。円周の長さを「lr[m]」としたとき、これの算出のための公式は以下のとおりです。

扇形の弧の長さは上の式に角度の割合を乗じたものとなります。注意すべきは下の式での「θ」は360°に対する割合であり度数法によるものです。単位は必然的に「°(度)」となります。

このことからわかるとおり、円弧を利用する弧度法では円周と密接な関係をもつ「π」を必然的に利用することとなります。
④弧度法と度数法の換算
弧度法の定義と円周率「π」との関係を説明しましたが、いくら表現方法が違っていたとしても、弧度法と度数法はいずれも角度を表現する方法ですので、相互に換算することが可能です。
弧度法の計算式と先程出てきた扇形の弧の長さの計算式から導くことが可能です。

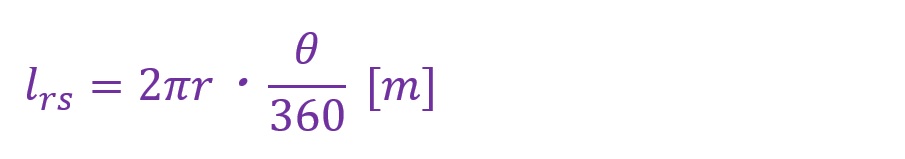
弧度法の式に扇形の弧の長さの計算式をそのまま代入可能ですので、これを計算します。

ここで得られた式が弧度法と度数法の変換式となります。度数法の「θ°」に「π/180」を乗じたものが弧度法の角度表現になるということが、式からよみとれます。
三角関数では、なにかとこの弧度法を用います。弧度法で表記された角度がどれくらいなのか感覚でわかる程度まで理解できると、これからの計算が楽になります。
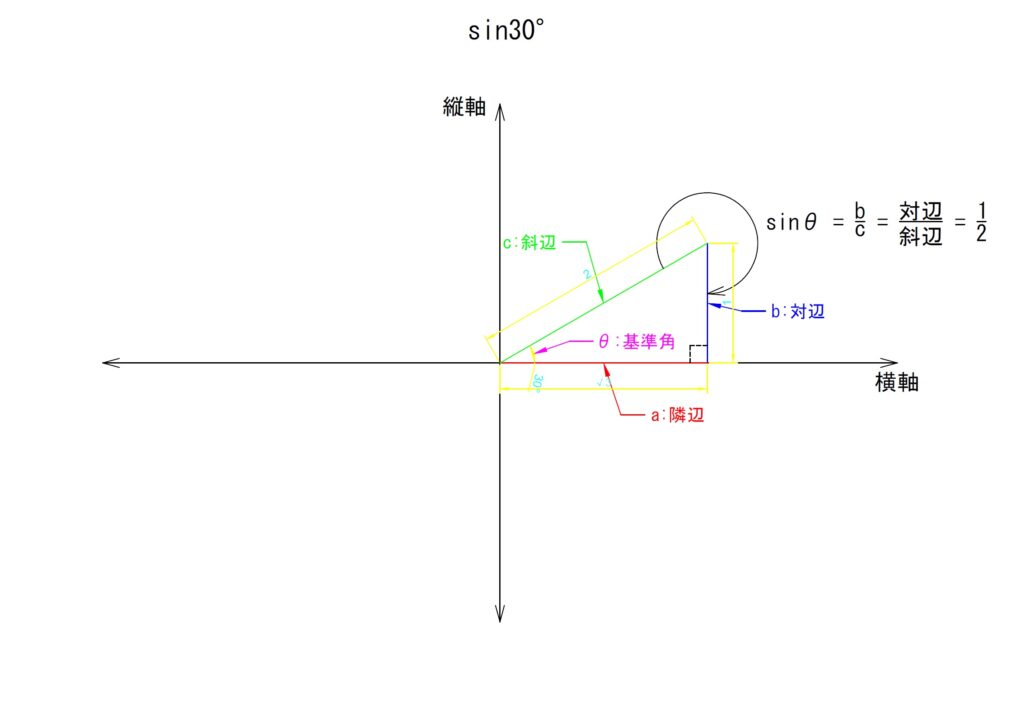
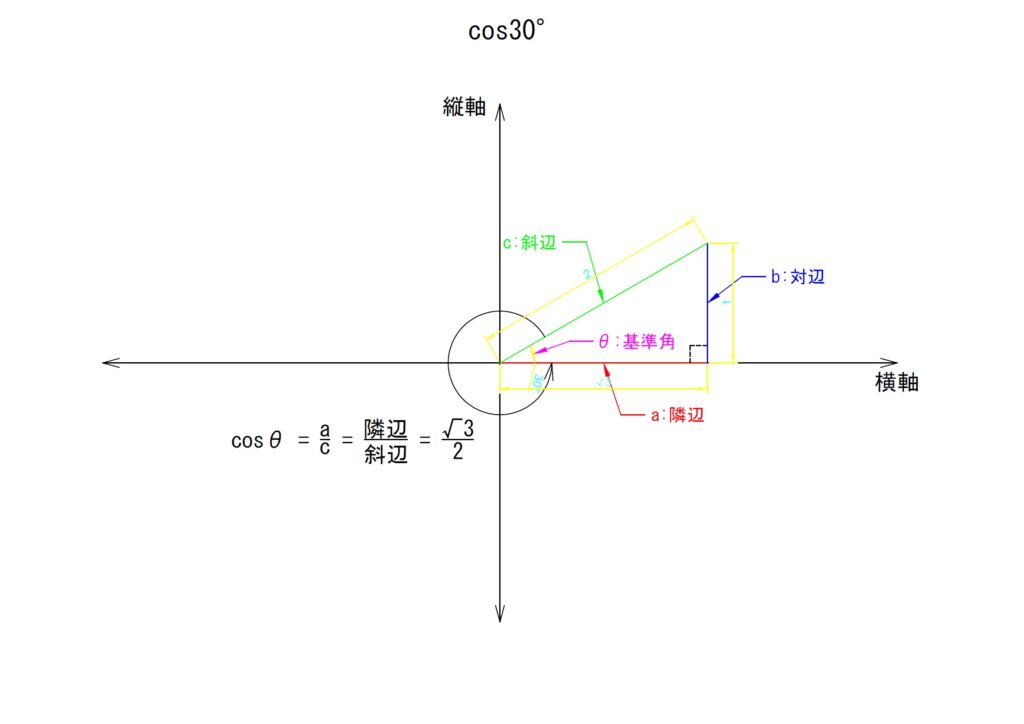
5)頻出の角度
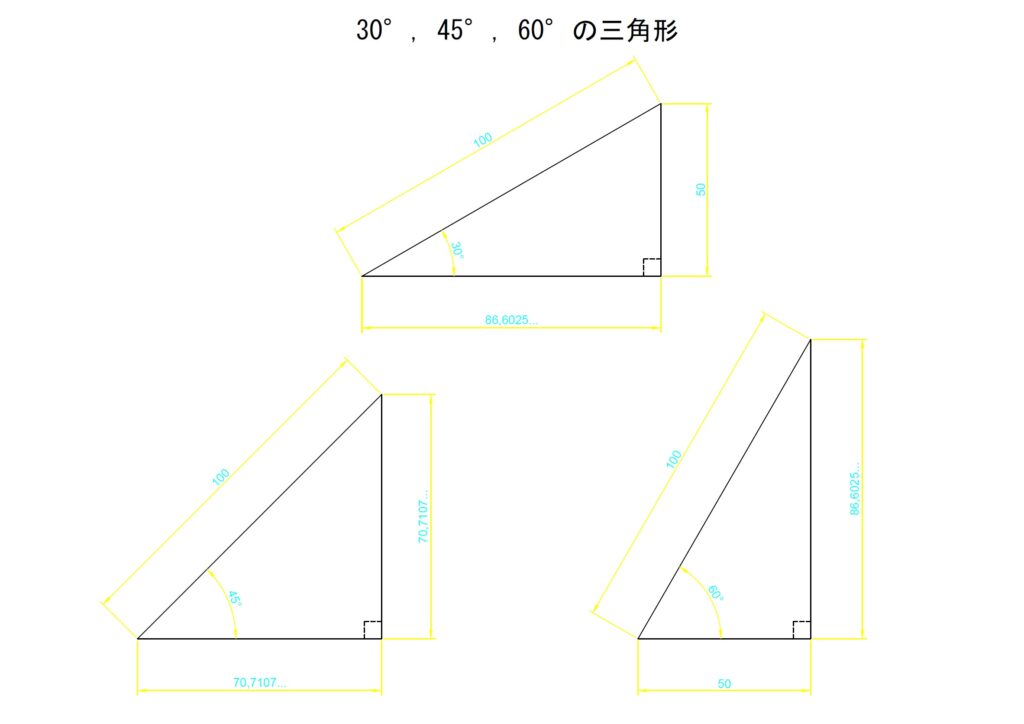
三角関数を学習するときに非常に頻繁にとりあげられる角度があります。それが「30°」「45°」「60°」の角度です。これらは三角関数を取り扱うときに頻繁に例にあげられる角度であり、必ずと言っていいほど学習の導入部とされます。
「学ぶうえでの角度なんて何でもいいんじゃないか…」と思う人もいるかもしれませんが、以下の直角三角形では三角関数においてきりが良く(?)覚えやすい値となります。
これらの角度は表現上非常に都合が良いです。
まず、弧度法での表記ですが、先にあげた角度は以下のようにすっきりとした表現に収まります。



次に、三角関数の各値でも平方根こそでるものの、かなりシンプルにまとまった形となります。以下、列挙します。
30°について
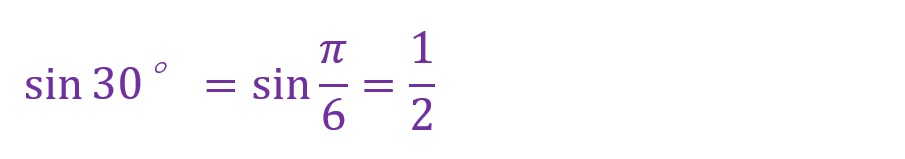
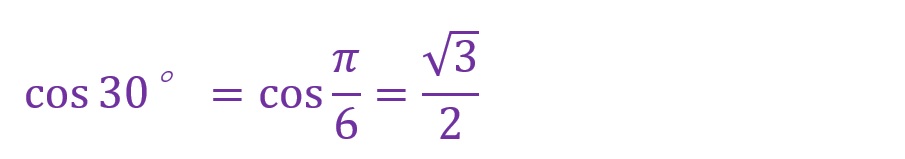
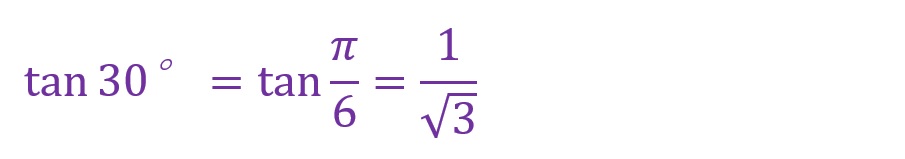
45°について
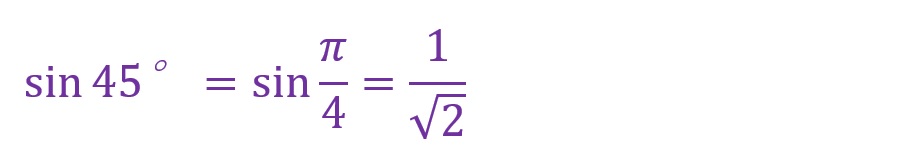
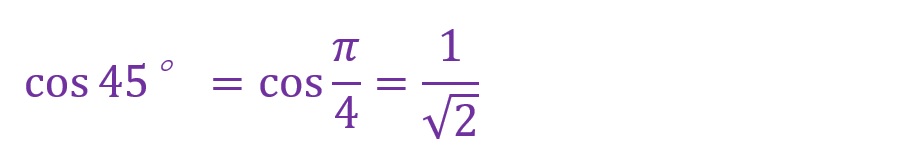
60°について
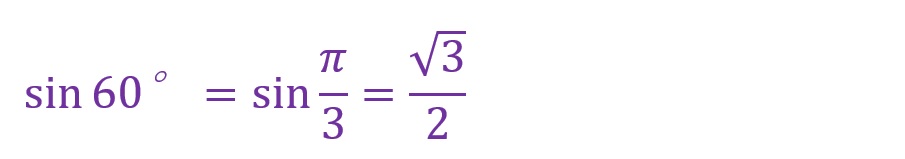
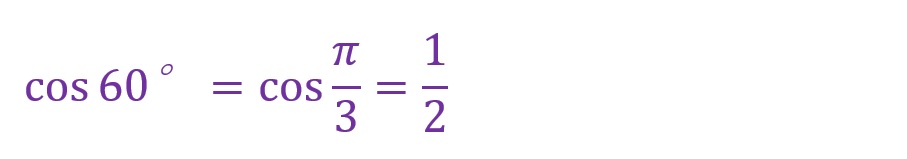
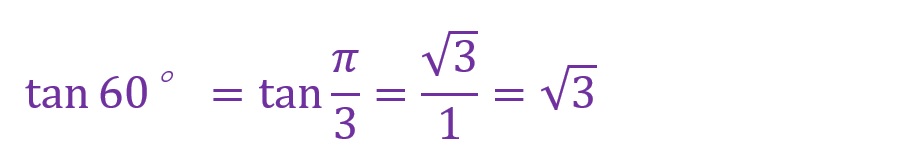
少しくわしく表しても1行に収まるくらいシンプルです。弧度法でもすっきり、三角関数でもすっきりな角度はこれらくらいです。
他の角度では平方根ですら表しきれないような煩雑な値となり、三角関数を学習するにあたって、上記のような角度ほど適してはいません。
また、今とりあげた角度に加えて0°と90°での三角関数を把握することで三角関数自体がどのような性質のものなのかをつかむことができます。
0°について

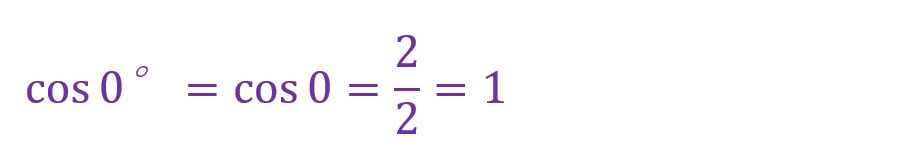
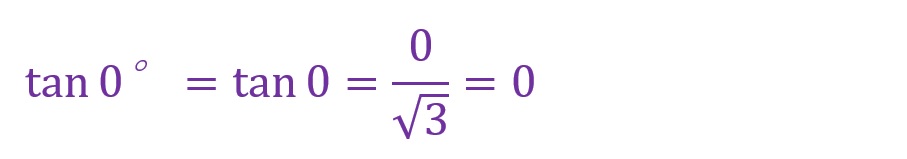
90°について
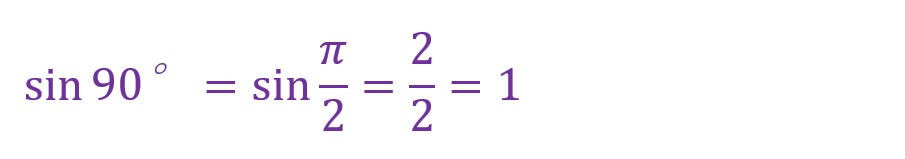
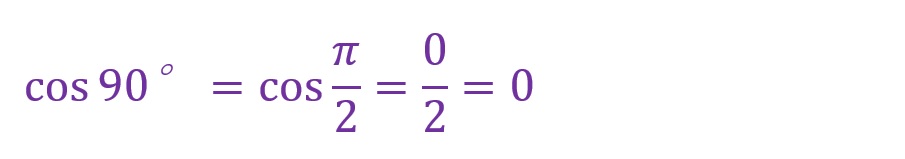

tan90°は分母が「0」になるため定義はできません。
ここまでにとりあげた角度における三角関数に対して理解していくことで、まず「三角関数がなにを言わんとしているのか」や「三角関数をどのように扱えばいいのか」といったことは充分に読み取れるでしょう。
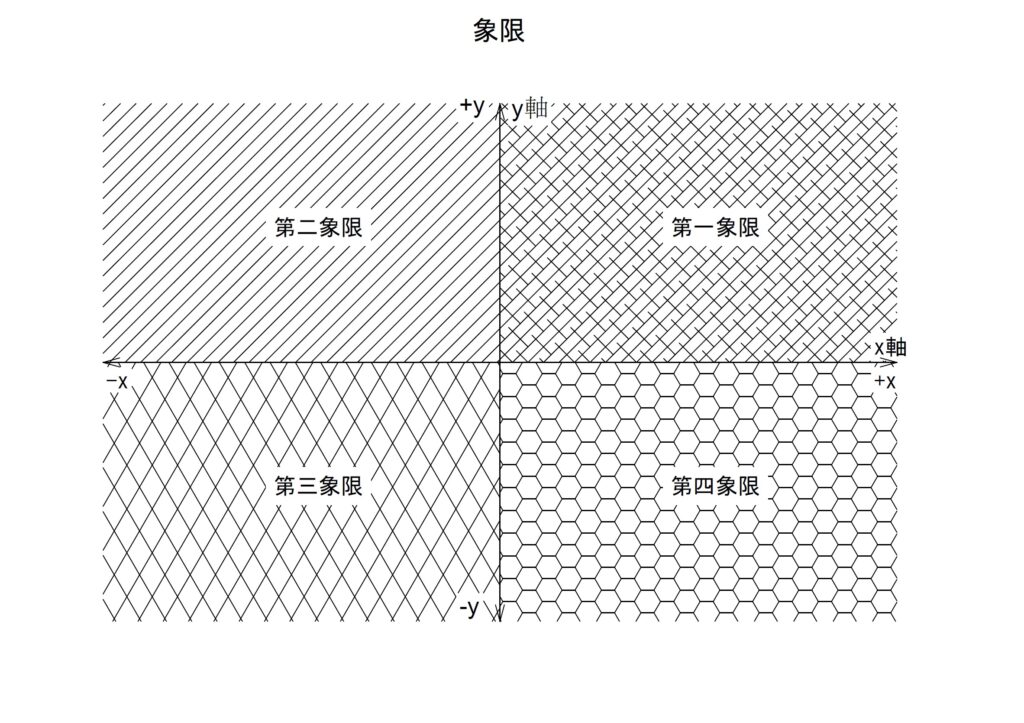
6)象限
基準となる角で形成される直角三角形をもとに比を割り出す三角関数では「象限」という概念が必要になります。この考え方はこの他に「複素数」などでも必要になります。
「象限」には四つの区分けがあります。グラフなどでよく見かける、縦軸と横軸で十文字に区切られた各区画を象限として扱います。
各々「第一象限」「第二象限」「第三象限」「第四象限」となります。直角三角形の斜辺がどの象限にあるかが計算結果の「符号」に影響します。
象限の順番はそのまま角度の増加方向と一致します。つまり左回りに「第一象限」「第二象限」「第三象限」「第四象限」となっています。
以降、各象限での値の変化をみていきます。わかりやすさのために「θ=30°」の整数倍の角度で各々の値を追いかけていきます。さらに、わかりやすさのために円の半径を「2」として計算を実行します。
なおここからは弧度法の表現を中心に表記します。つまり「θ=30°=π/6[rad]」を使用します。
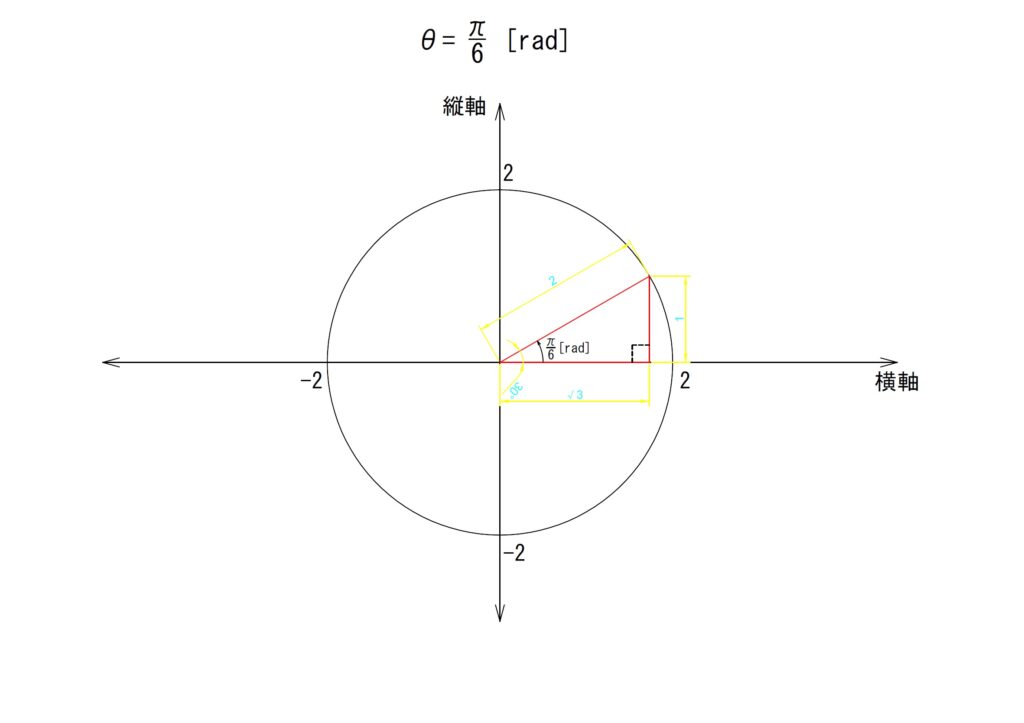
a.θ✕1
倍数は「1」つまり「θ=π/6[rad]」をみてみます。
第一象限の範囲に収まる角度です。単純に計算できます。



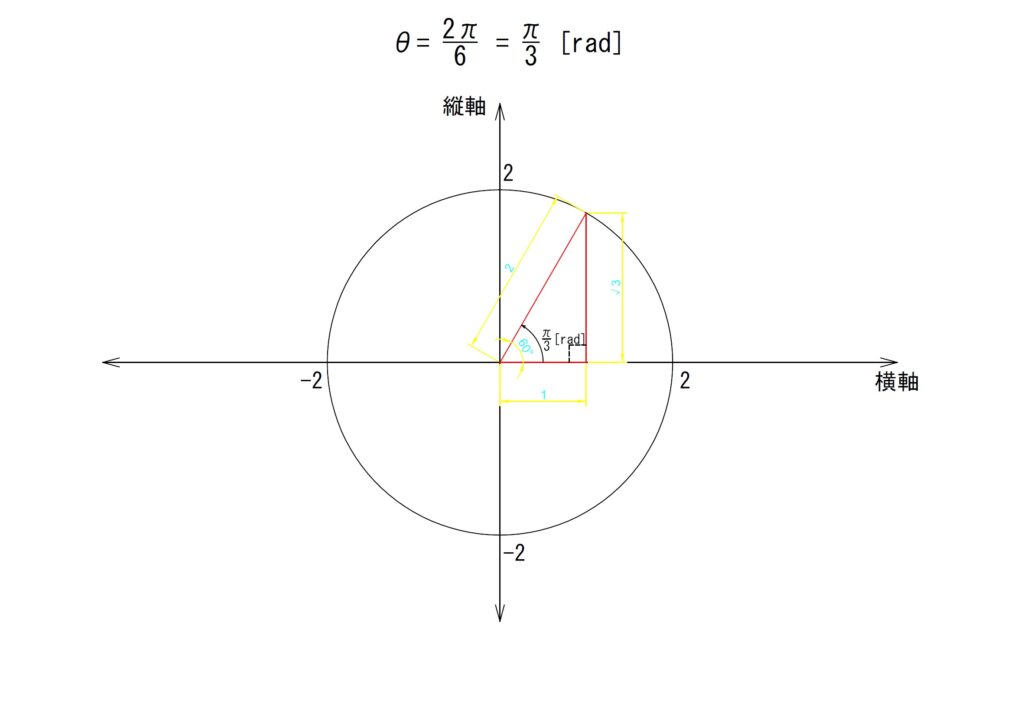
b.θ✕2
角度を2倍します。「θ=2✕(π/6)=π/3[rad]」となります。
まだ、第一象限内に収まっています。単純に計算します。
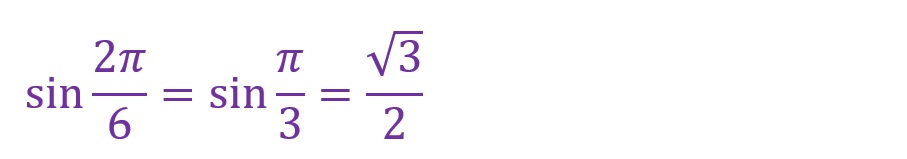
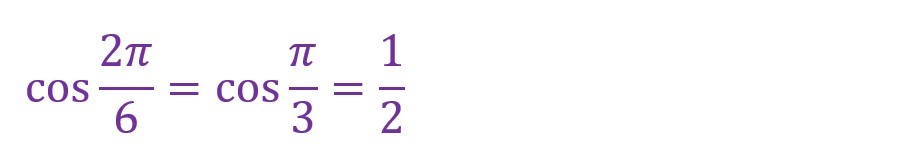
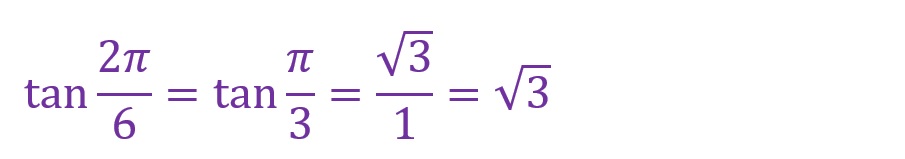
c.θ✕3
角度を3倍します。「θ=3✕(π/6)=π/2[rad]」となります。度数法では90°になる位置で、第一象限と第二象限の中間、つまり縦軸上に重なる角度です。見た目には三角形がありませんが、隣辺が「0」になったものと考えてください。
これも今までの計算と変わりありません。
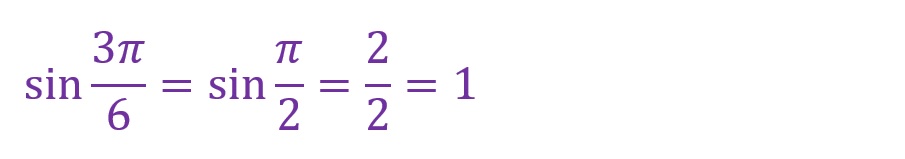
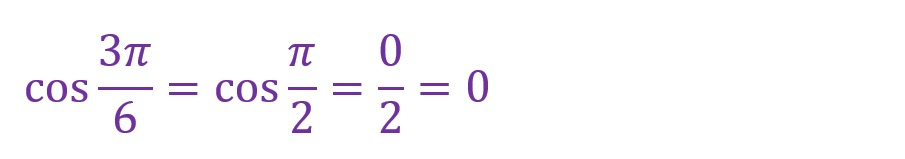

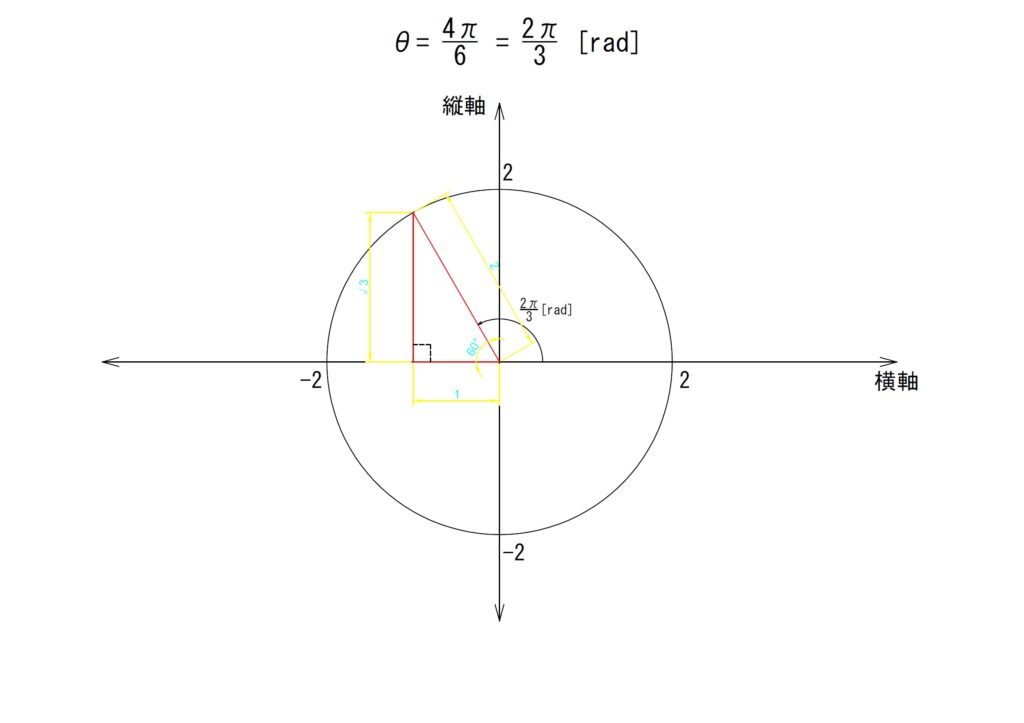
d.θ✕4
角度を4倍します。
「θ=4✕(π/6)=(4π)/6=(2π)/3[rad]」となります。第二象限内に斜辺がくることとなりました。この場合直角三角形はどのようになるのでしょうか。
結論としては単純であり、最寄りの横軸からの垂線を以て直角三角形を形成します。以下の図のようになります。
では、角度はどのようにみれば良いのでしょうか。「(2π)/3[rad]」は「π/2[rad]」以上であり直角三角形の外の角度になってしまいます。
こちらも最寄りの横軸からの角度をみると良いです。すると、「π/3[rad]」の場合と同じ形で向きだけが違う直角三角形が形成されていることがわかります。
上の図では横軸成分が負方向(マイナス側)で縦軸成分が正方向(プラス側)の長方形内に直角三角形が形成されています。斜辺には正負の概念はありません。「sinθ=対辺/斜辺」「cosθ=隣辺/斜辺」「tanθ=対辺/隣辺」ですので「θ=(2π)/3)[rad]」では以下の計算となります。
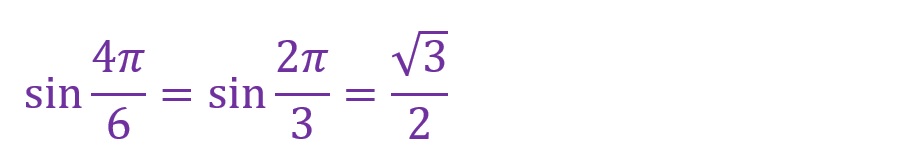
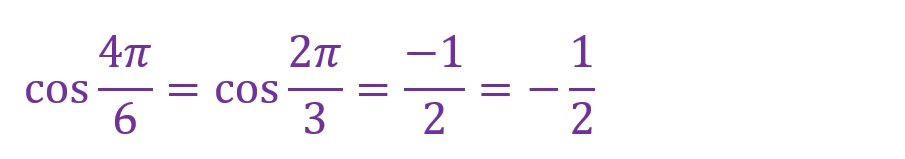
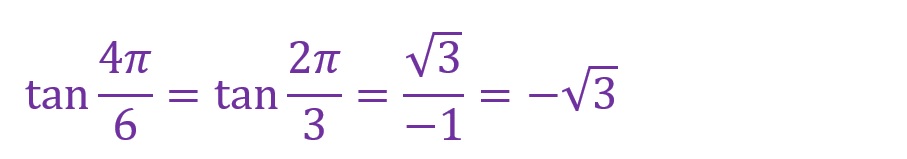
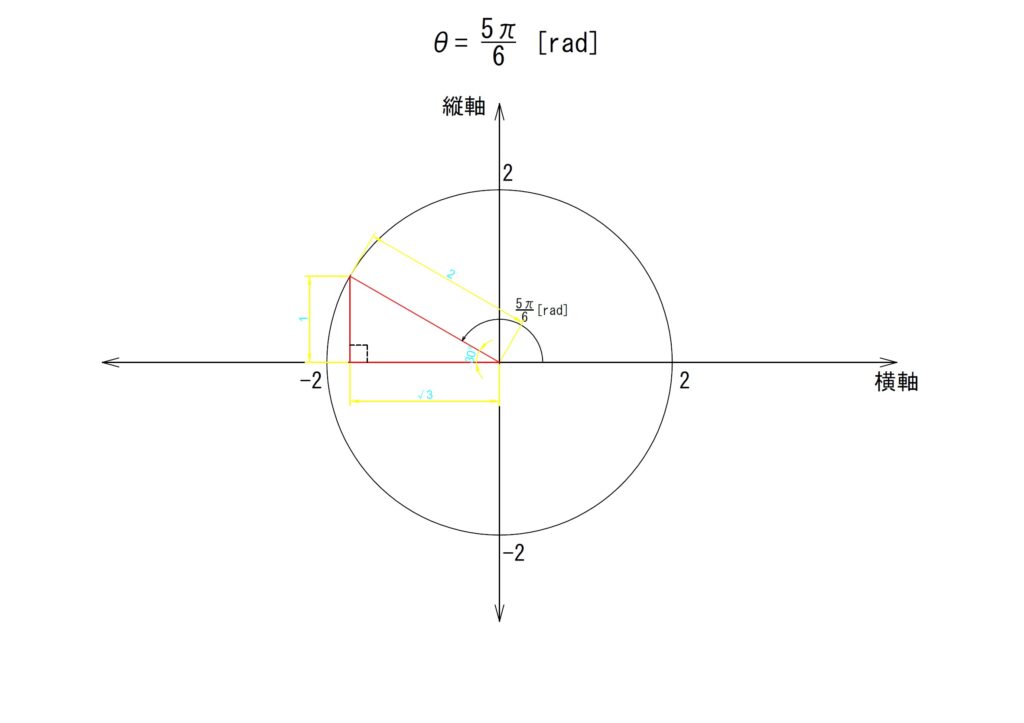
e.θ✕5
角度を5倍します。
「θ=5✕(π/6)=(5π)/6[rad]」となります。第二象限内に斜辺がくることとなりました。4倍のときと同様に横軸からの垂線を以て直角三角形を形成します。
最寄りの横軸からの角度をみると、「π/6[rad]」の場合と同じ形で向きだけが違う直角三角形が形成されていることがわかります。
上の図でも「4倍」のときと同様の考え方です。横軸成分が負方向(マイナス側)で縦軸成分が正方向(プラス側)の長方形内に直角三角形が形成されています。斜辺には正負の概念はありません。「sinθ=対辺/斜辺」となることから「θ=(5π)/6)[rad]」では以下の計算となります。

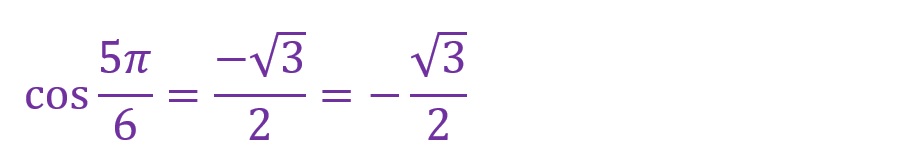
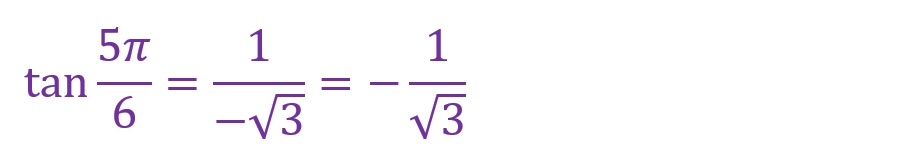
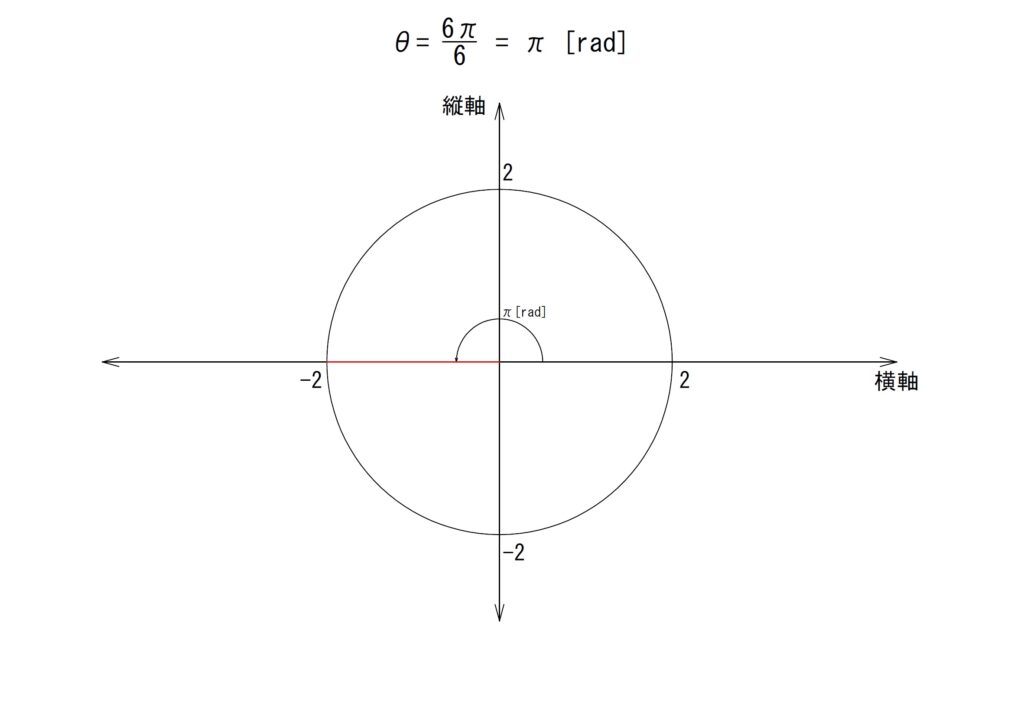
f.θ✕6
角度を6倍します。
「θ=6✕(π/6)=π[rad]」となります。ちょうど180°の位置であり、横軸に重なる角度となります。見た目には三角形がありませんが、対辺が「0」になったものと考えてください。
横軸に関する部分が負方向であることを失念しないように気をつけます。
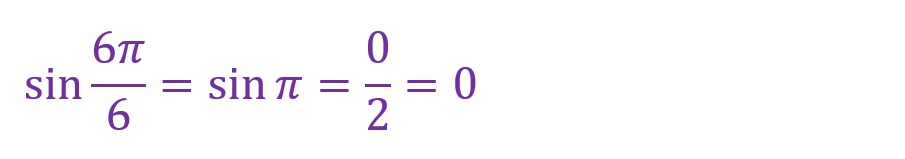
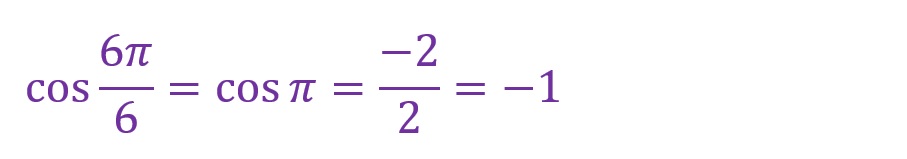
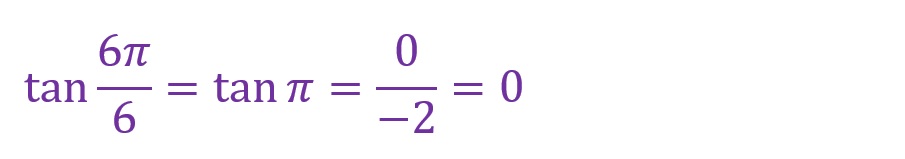
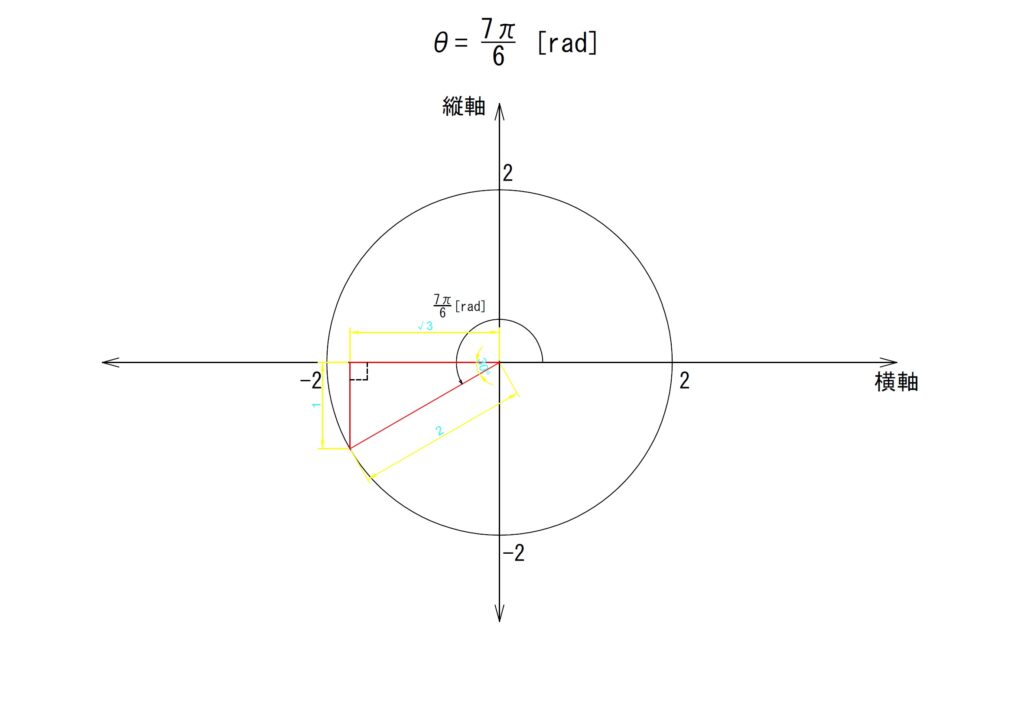
g.θ✕7
角度を7倍します。
「θ=7✕(π/6)=(7π)/6[rad]」となります。第三象限内に斜辺がくることとなりました。これまでと同様に横軸からの垂線を以て直角三角形を形成しますが、垂線は紙面(画面)の下方向へ伸びることとなります。
最寄りの横軸からの角度をみると、「π/6[rad]」の場合と同じ形で上下左右の向きが違う直角三角形が形成されていることがわかります。
上の図でも「4倍」や「5倍」のときと同様の考え方ですが、横軸成分が負方向(マイナス側)であることに加え、縦軸成分も負方向(マイナス側)の長方形内に直角三角形が形成されています。縦横軸のどちらにおいても負の値になることに注意してください。
結果、「θ=(7π)/6)[rad]」は以下の計算となります。
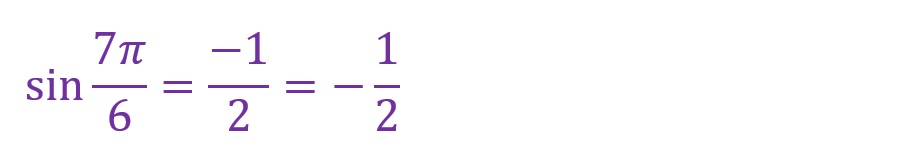
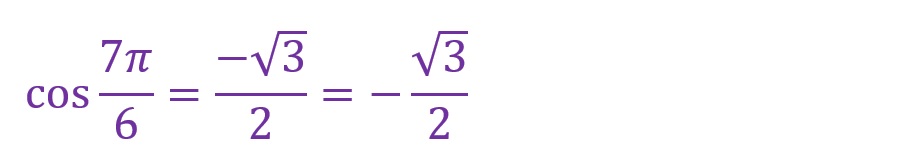
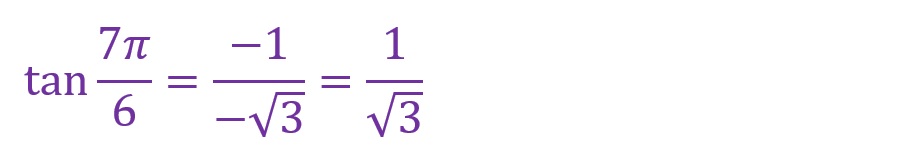
h.θ✕8
角度を8倍します。
「θ=8✕(π/6)=(8π)/6=(4π)/3[rad]」となります。ここでも第三象限内に斜辺がくることとなりました。考え方は「7倍」のときと同じです。
最寄りの横軸からの角度をみると、「π/3[rad]」の場合と同じ形で上下左右の向きが違う直角三角形が形成されていることがわかります。
計算方法も「7倍」のときと同様です。
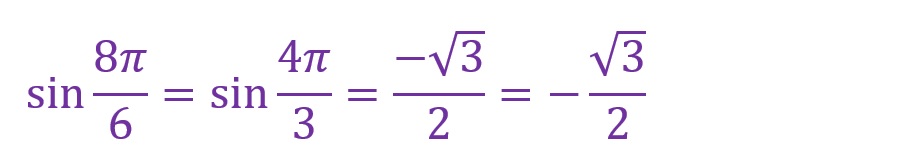
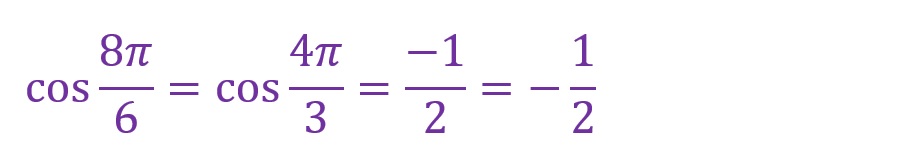
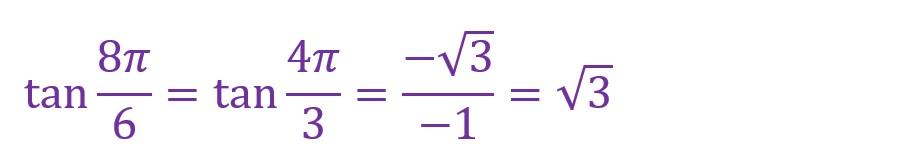
i.θ✕9
角度を9倍します。
「θ=9✕(π/6)=(9π)/6=(3π)/2[rad]」となります。度数法で表すと270°です。縦軸に重なる角度です。見た目には三角形がありませんが、隣辺が「0」になったものと考えてください。
縦軸に重なり、負方向へ伸びる直線となります。
符号に注意して計算します。斜辺と対辺が同一であることから以下の計算になります。
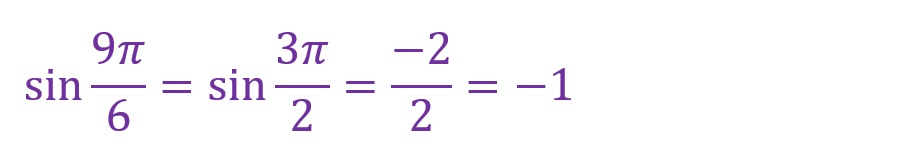
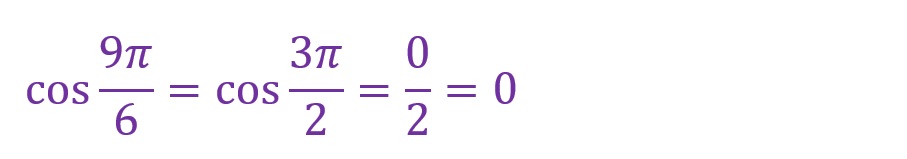

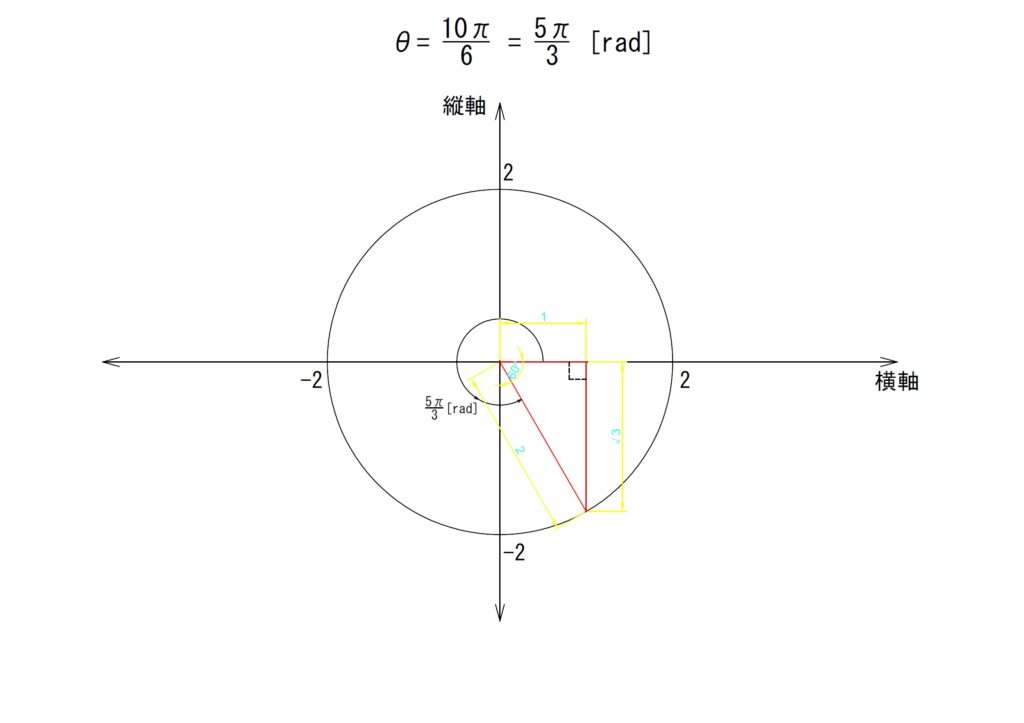
j.θ✕10
角度を10倍します。
「θ=10✕(π/6)=(10π)/6=(5π)/3[rad]」となります。斜辺は第四象限にくることとなりました。
最寄りの横軸からの角度をみると、「π/3[rad]」の直角三角形と横軸で線対称の直角三角形が形成されていることがわかります。
結局はここでの計算も第三象限のときと同様です。ただし、縦軸成分のみが負方向であり、横軸成分は正方向であることに注意してください。
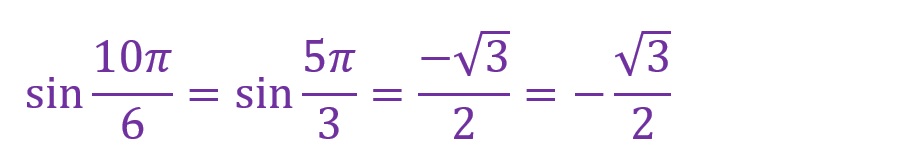
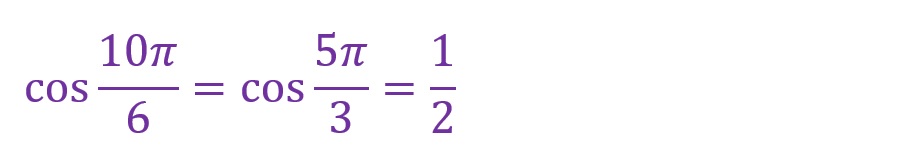
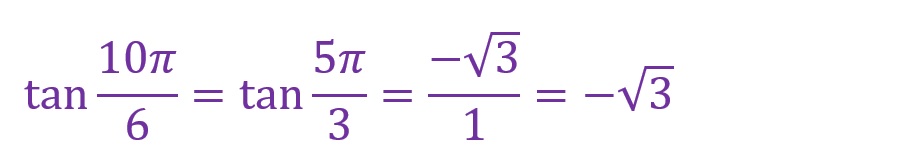
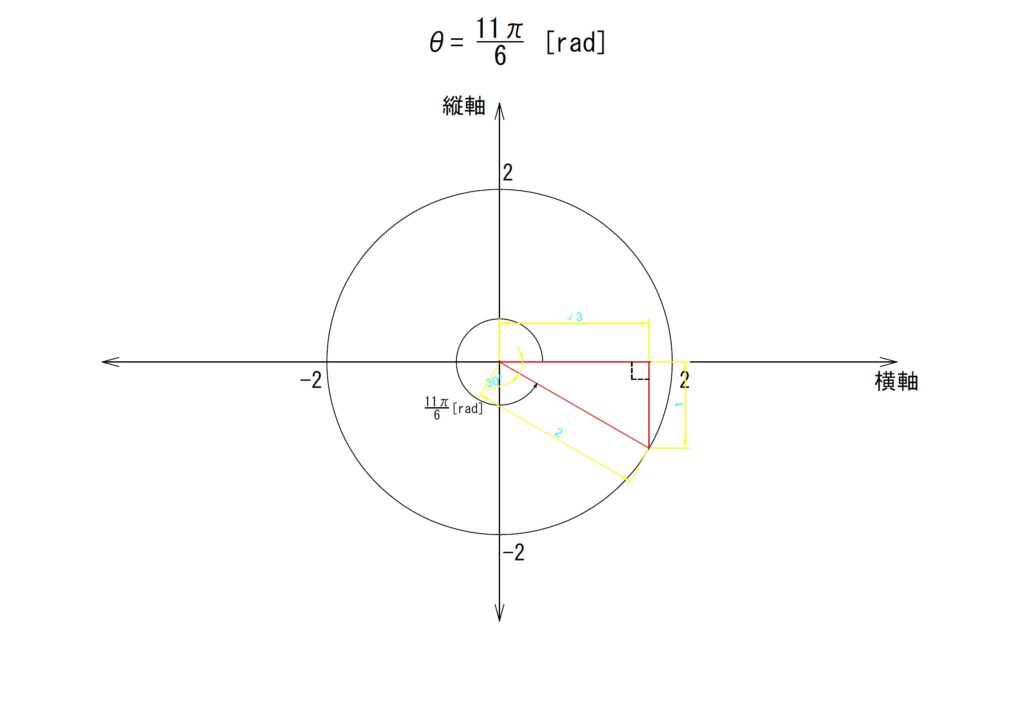
k.θ✕11
角度を11倍します。
「θ=11✕(π/6)=(11π)/6[rad]」となります。斜辺は依然第四象限にあります。
最寄りの横軸からの角度をみると、「π/6[rad]」の直角三角形と横軸で線対称の直角三角形が形成されていることがわかります。
縦軸成分のみが負方向です。計算結果は以下です。
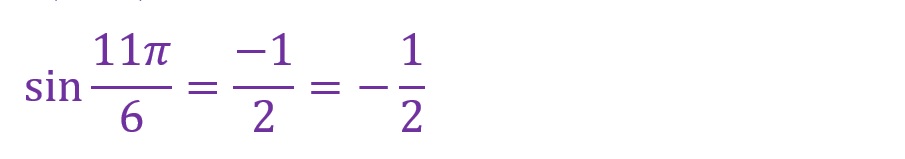

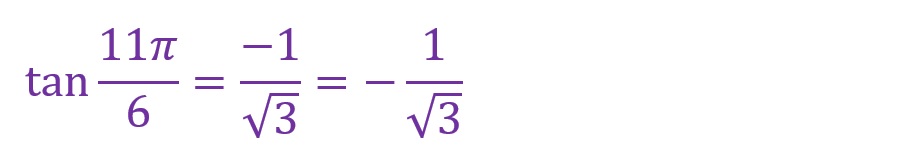
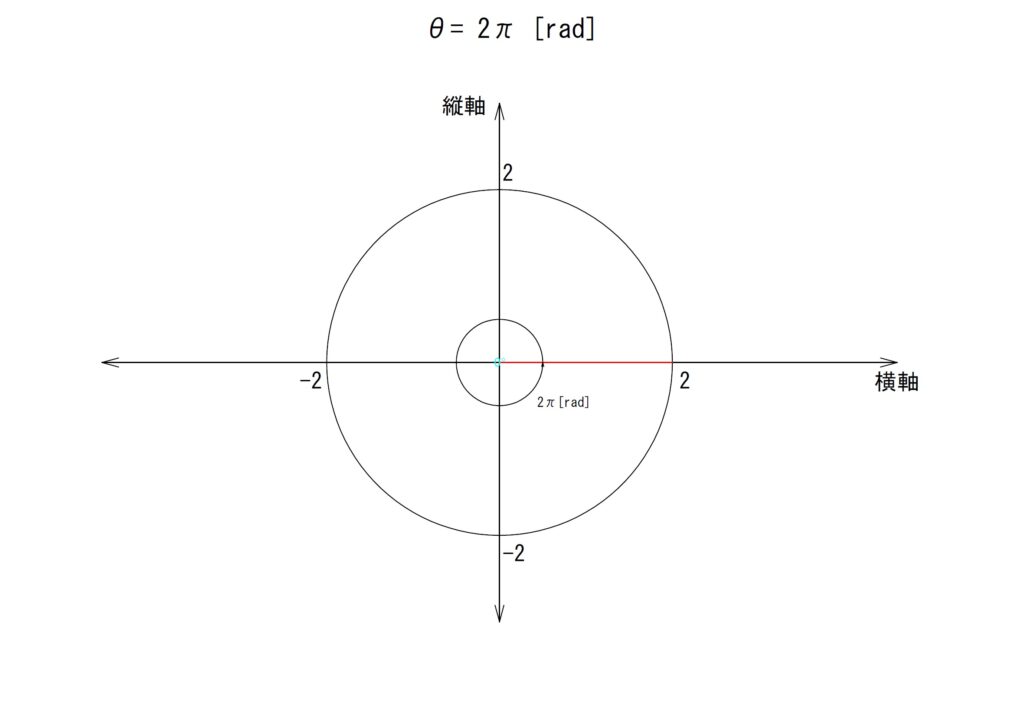
l.θ✕12
角度を12倍します。
「θ=12✕(π/6)=(12π)/6=2π[rad]」となります。斜辺が一周したことになります。角度として「2π=0[rad]と考えることができます。見た目には三角形がありませんが、対辺が「0」になったものと考えてください。
斜辺は横軸と重なる位置にあります。横軸に重なるのは「6倍」のときもそうですが、この場合とは方向が逆です。
計算としては以下のようになります。
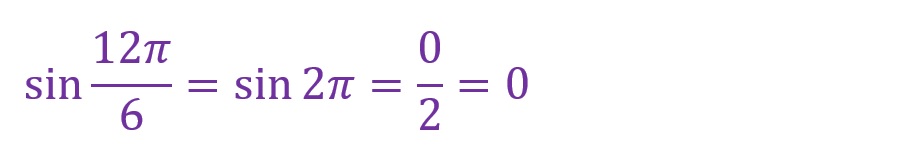
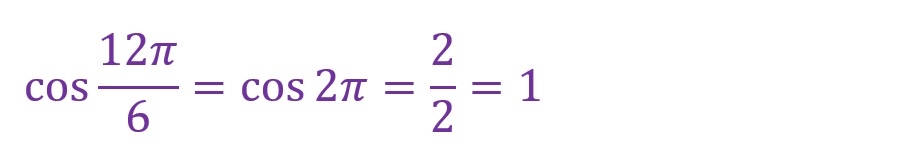
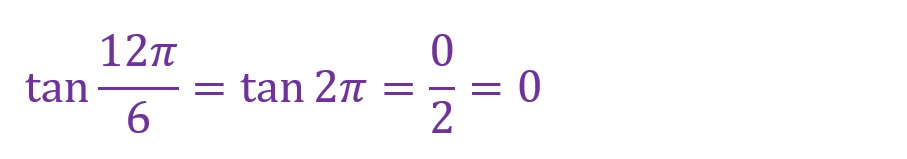
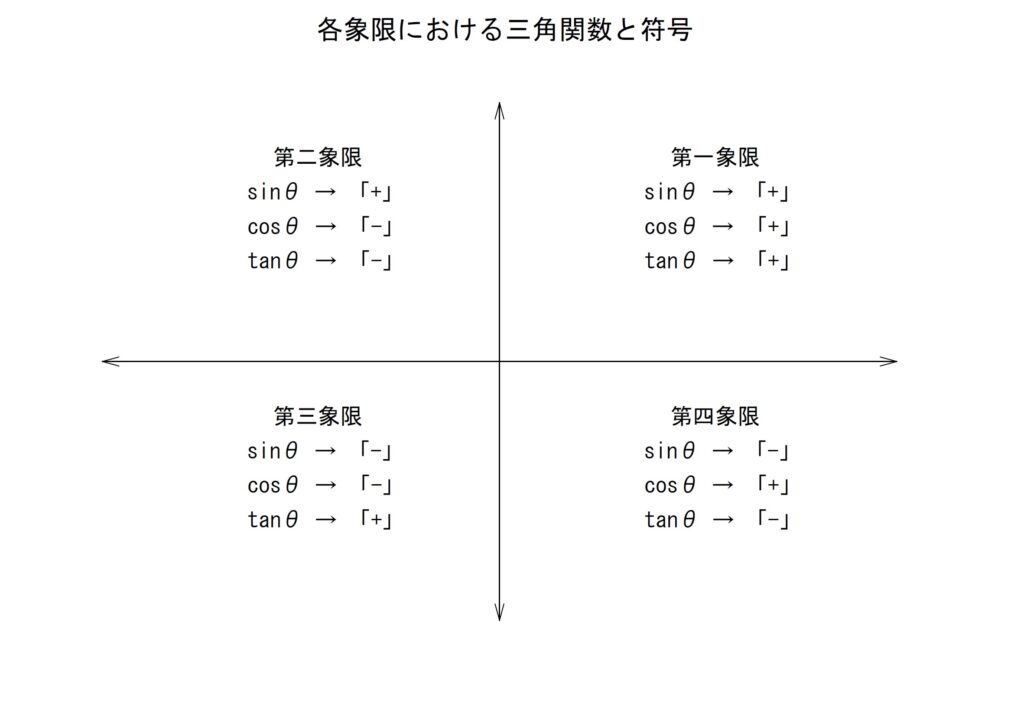
7)各象限での符号
ここまで三角関数の象限における変化を追いました。どの象限の角でどの三角関数を求めるかによって符号が変化しました。符号の変化を象限と三角関数で分けると以下の図のようになります。
縦軸成分と横軸成分の符号が影響することはこれまでの結果から明らかです。
8)三角関数グラフ
三角関数において、その計算方法および象限による符号の変化について説明しました。
ここまでを理解すると、各三角関数をグラフに表すことが可能になります。せっかくですので、前の項「7)」で算出した値をグラフ化してみます。
4.三角関数応用
ここまで三角関数の基礎部分を説明しました。特に直角三角形を前提とした「π/6[rad](=30°)」や「π/4[rad](=45°)」または「π/3[rad](=60°)」など、有名角といわれる角度を例に挙げた説明でした。
では、三角関数は直角三角形の有名角でしか使えない関数なのでしょうか。
もちろんそんなこともなく、三角関数は応用することで直角三角形以外でも有名角以外でも利用可能です。
三角関数を応用することで計算可能となる幅が広がります。ここではそのような三角関数の応用方法について説明します。
1)正弦定理と余弦定理
三角関数で利用する三角形は直角三角形であるということをこれまで説明してきました。これを逆にいうと、直角三角形でなければ一辺の長さや辺の比が算出できないということになります。
しかし、直角三角形でなくても三角関数を応用することで一辺の長さや辺の比を算出することができます。それが以下に説明する「正弦定理」と「余弦定理」になります。
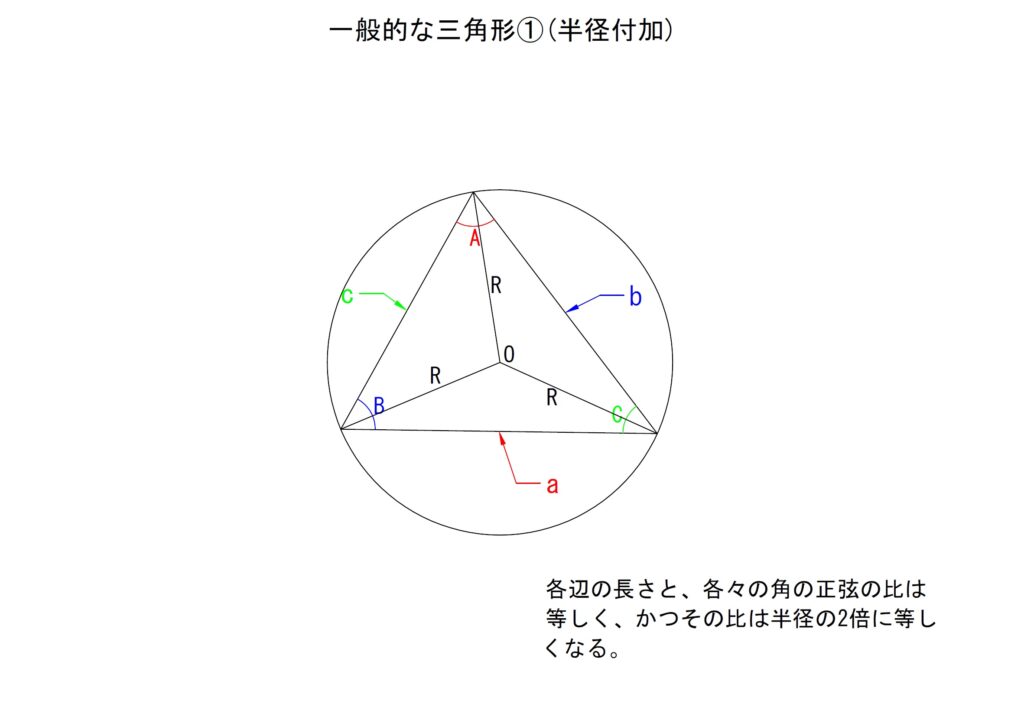
a.正弦定理
以下の図のような三角形があるとします。
上図の三角形は直角三角形ではありません。このような三角形における各辺と角度の関係がわかると三角関数を応用することができるようになります。
先の三角形に以下のように図を付け加えます。
上図と円周角の定理から以下の式が導き出されます。
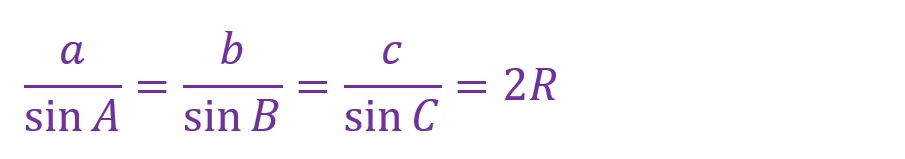
上の式で表される定理を「正弦定理」といいます。なお、「A」「B」「C」は三角形の各々の角を、「a」「b」「c」は各々の辺を表します。さらに「R」は外接円の半径を表しています。
この式の意味するところは、『各々の角における正弦(sinθ)と向かい合う辺の比は各々等しく、またその比は外接円の半径の2倍(直径)に等しい』ということです。
この定理の使い方を以下の例題にて記載します。長さの単位は「ミリメートル[mm]」とします。
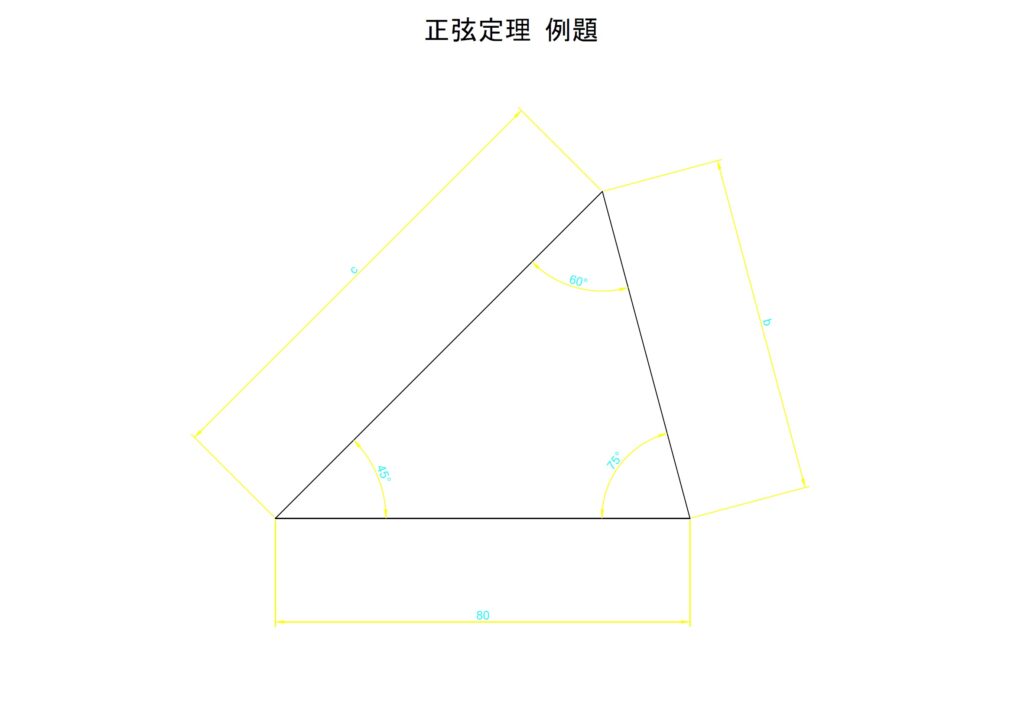
例題
下の三角形におけるbの長さを算出
上の三角形でまずわかることは∠Aの正弦(sinA)とaの比です。まずはsinAを計算します。
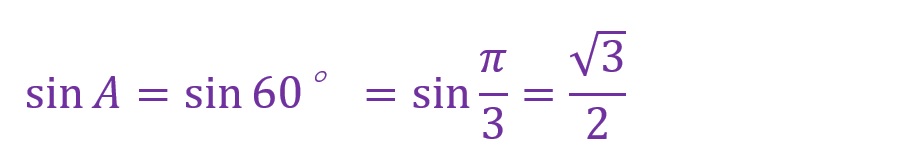
次にsinAと辺の比「a/sinA」を計算します。

sinBを算出します。
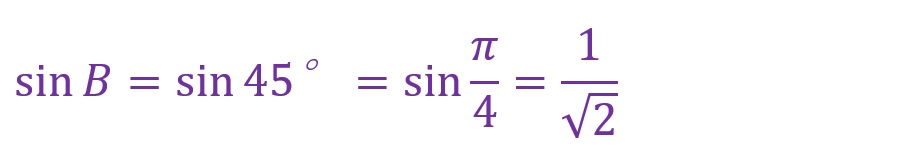
ここで「各々の角における正弦(sinθ)と向かい合う辺の比は各々等しい」ことから以下が得られます。
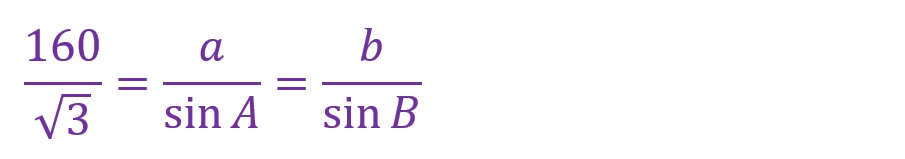


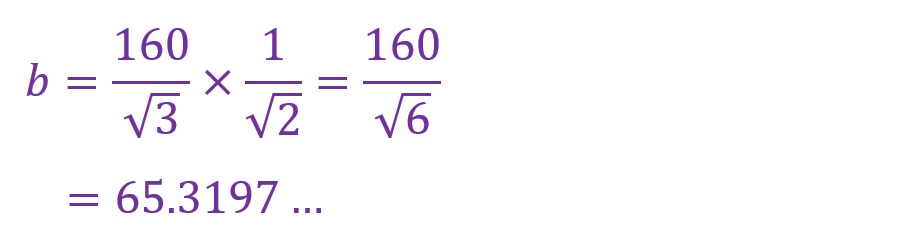
「b」の長さは65.3197…[mm]と算出されました。
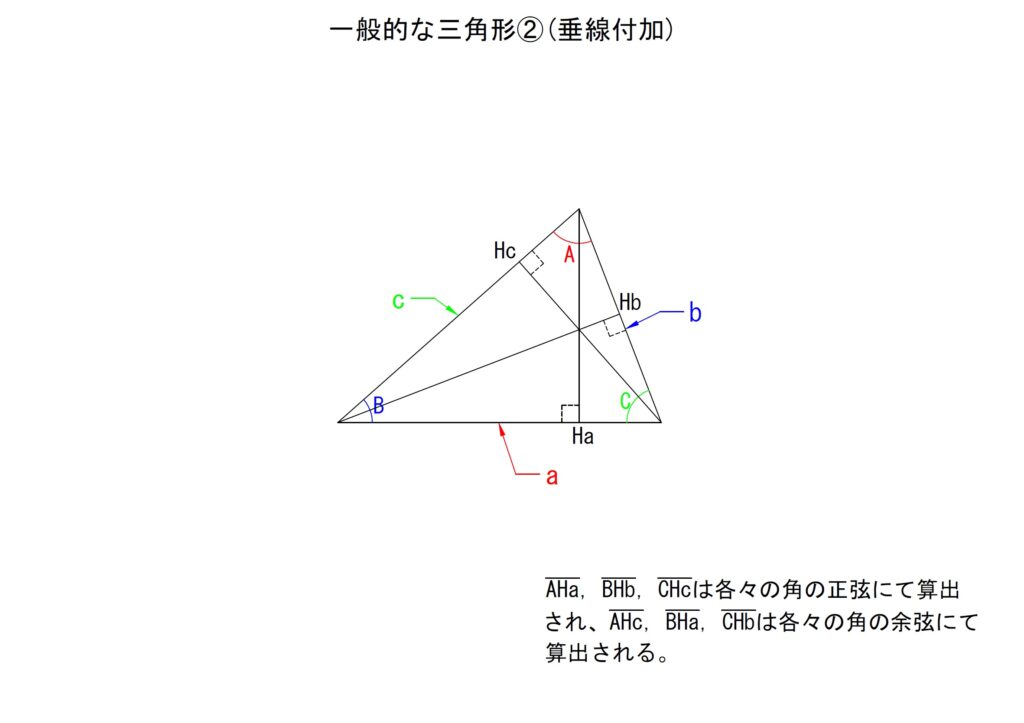
b.余弦定理
以下のような三角形があるとします。先ほどの正弦定理のときと同様に直角の存在しない三角形です。
上図の三角形もまた直角三角形ではありません。正弦定理同様に、このような三角形における各辺と角度の関係がわかれば、三角関数を正弦定理とは別の方法で応用することができるようになります。
先の三角形に以下のように図を付け加えます。
上図と三角比の基本公式「sin2θ+cos2θ=1」などから以下の三つの式が導き出されます。



式の中に三平方の定理が存在しており、またこの三平方の定理で算出する値から係数が付加された余弦を減算しています。
この定理の使い方を以下の例題にて記載します。
例題
下の三角形におけるbの長さを算出
《三角形の図:∠A=60°,a=80[mm],c=60[mm]》
この場合、余弦定理の公式に当てはめるだけで値を算出することができます。
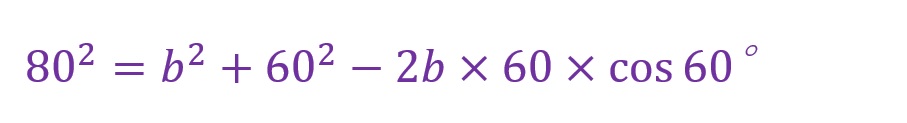
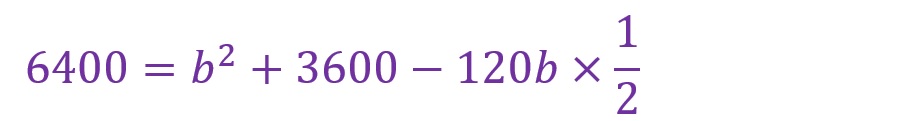

これを解の公式に当てはめます。解の公式は以下です。

記号の「b」が違う意味で存在するのでややこしいですが、上記に対して「x=b」と置き、「a=1」「b=-60」「c=-2800」として代入します。
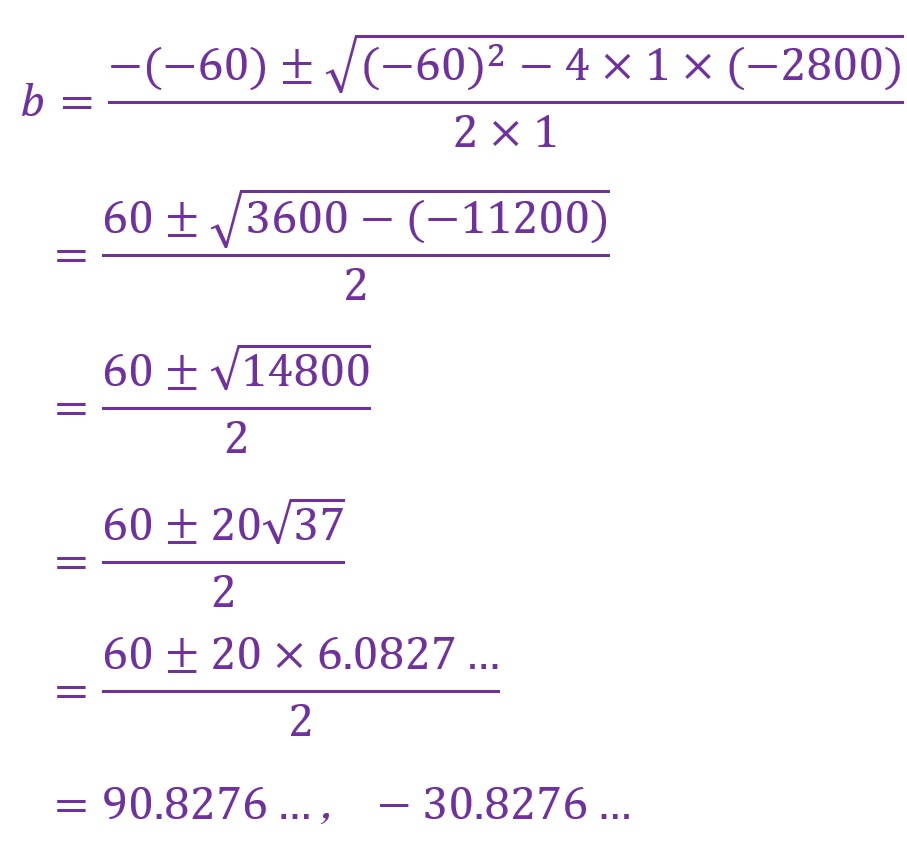
三角形にマイナスの直線は存在し得ないので「b」は90.8276…[mm]ということになります。
2)加法定理
ある角「α[rad]」と、ある角「β[rad]」を足し合わせたとき(加算)の三角関数における計算方法です。もちろん差し引き(減算)にも利用可能です。
極端な話ではありますが、この定理を利用することにより「1°」の三角関数がわかれば全ての整数による三角関数が算出可能ということになります。
以下が「加法定理」の式です。
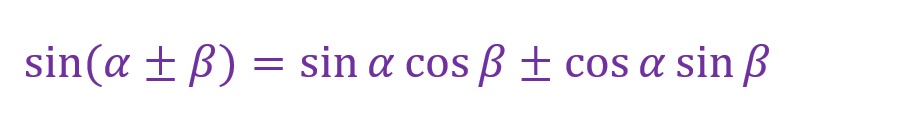
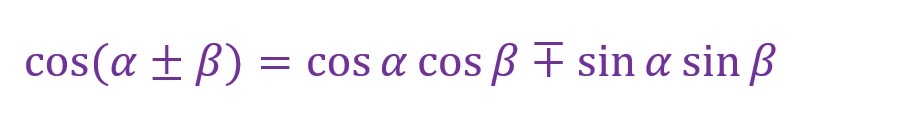
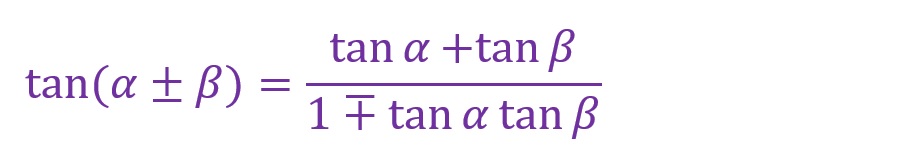
三角関数の角度はそのまま加減算できないということがよくわかる式となっています。たとえば、「sin(30°+45°)」ならばなんとなく「sin30°+sin45°」として計算したくなりますが、そうはならないということです。
なお、数式によって加減算の符号が逆になっているので充分注意が必要です。
この定理の使い方を以下の例題にて記載します。正弦の一例をあげます。
例題
①以下の正弦を計算

加法定理を適用します。
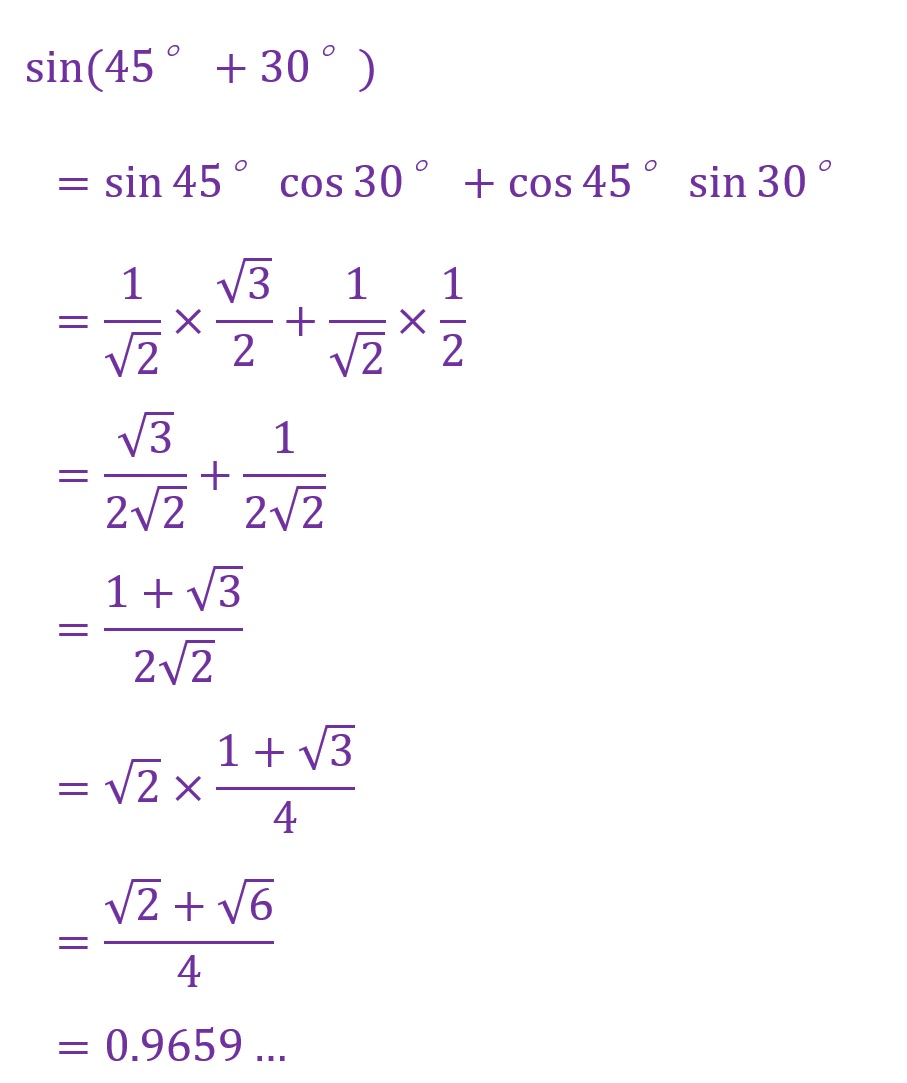
「sin(45°+30°)」は「0.9659…」という解答が得られました。
次いで、この定理が正しく機能しているか否かがよく分かる例をあげます。加算する角度を「30°」と「60°」とします。正弦を計算したときに果たして「sin90°」と等しくなるでしょうか。
②以下の正弦を計算

「sin(30°+60°)」は「1」という解答が得られました。加法定理が正しく機能していることがよくわかる例です。
3)倍角の公式と半角の公式
加法定理において角度が倍になったり半分になったりする場合、簡素化した式を用いることが可能になります。各々を以下に記載します。
a.倍角の公式
加法定理において角度が「α=β」であるときに倍角の公式を用いることができます。
倍角の公式は以下のようになります。

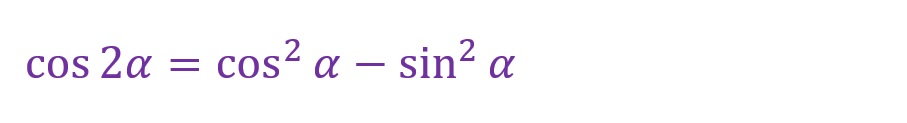

比較的複雑な加法定理がかなりシンプルな形になりました。注意すべきは余弦や正接で2乗が出てきていることです。
導き出した余弦や正接の結果を2乗するということを忘れないようにしましょう。
b.半角の公式
三角関数において、角度を2倍にする公式があれば1/2倍する公式もあります。
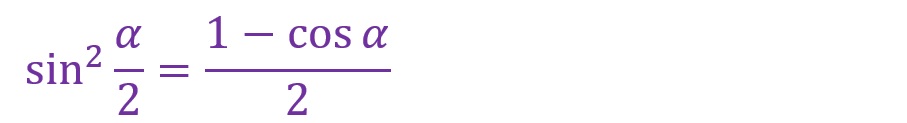

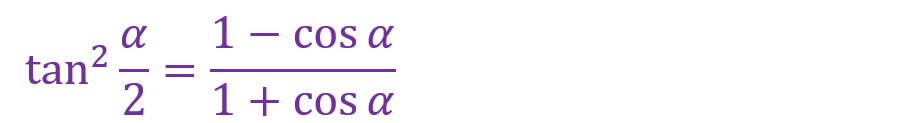
左辺が2乗になっていることに関して、倍角の公式と同じく注意が必要です。また、半角の公式は倍角の公式から比較的容易に導出できます。
4.交流計算では必須
ここまで、三平方の定理と三角関数について説明をしてきましてが、電気知識の習得においてこの概念を放置しておくことはできません。もちろん、取り扱う電気が直流であったり、交流でもごく簡単な計算のみであるならば三角関数などの出番は無いかもしれません。
しかしながら、交流回路において扱うレベルが少し上がるとすぐにここで述べている考え方が必要となってくることも事実です。
たとえば、電気エネルギーの管理などでは当たり前のように「力率」という概念が登場します。これを計測する「力率計」というものには「cosφ」などという表記もみられるくらい直接的に三平方の定理や三角関数が関与してきます。当然のことながらここで述べている知識無しではこの計器をどのようによめば良いのかすらわからないということになります。
また交流回路上で、ある瞬間において負荷がどのようなエネルギー消費をしているのかを計上するのにも三平方の定理や三角関数の知識を要します。
少し考えただけでも簡単に例が出てくるくらい、ここで述べた内容が電気における特に交流計算においては無視できない概念であることがわかります。
ややこしくてとっつきにくい分野かもしれませんが、毎度述べているとおり焦らずにひとつひとつ理解していけば必ず道は開けます。一歩一歩着実に前に進みましょう。