1.三相交流の特徴について
三相交流回路に関する電圧の印加状態や電流の発生状態を以前に単相交流と三相交流の記事で説明していますが、今回はその特徴をもう少しだけ深く見ていきます。ここで説明する内容は三相交流回路独特のものであり、ここを理解していなければ三相交流における試験や実務で少々困る場合があるというものになります。
その知識とは、三相交流回路においては「相」と「線(線間)」があるという考え方です。とても重要な考えかたですので丁寧にみていきましょう。
では説明していきます。
2.「相」と「線」の概念
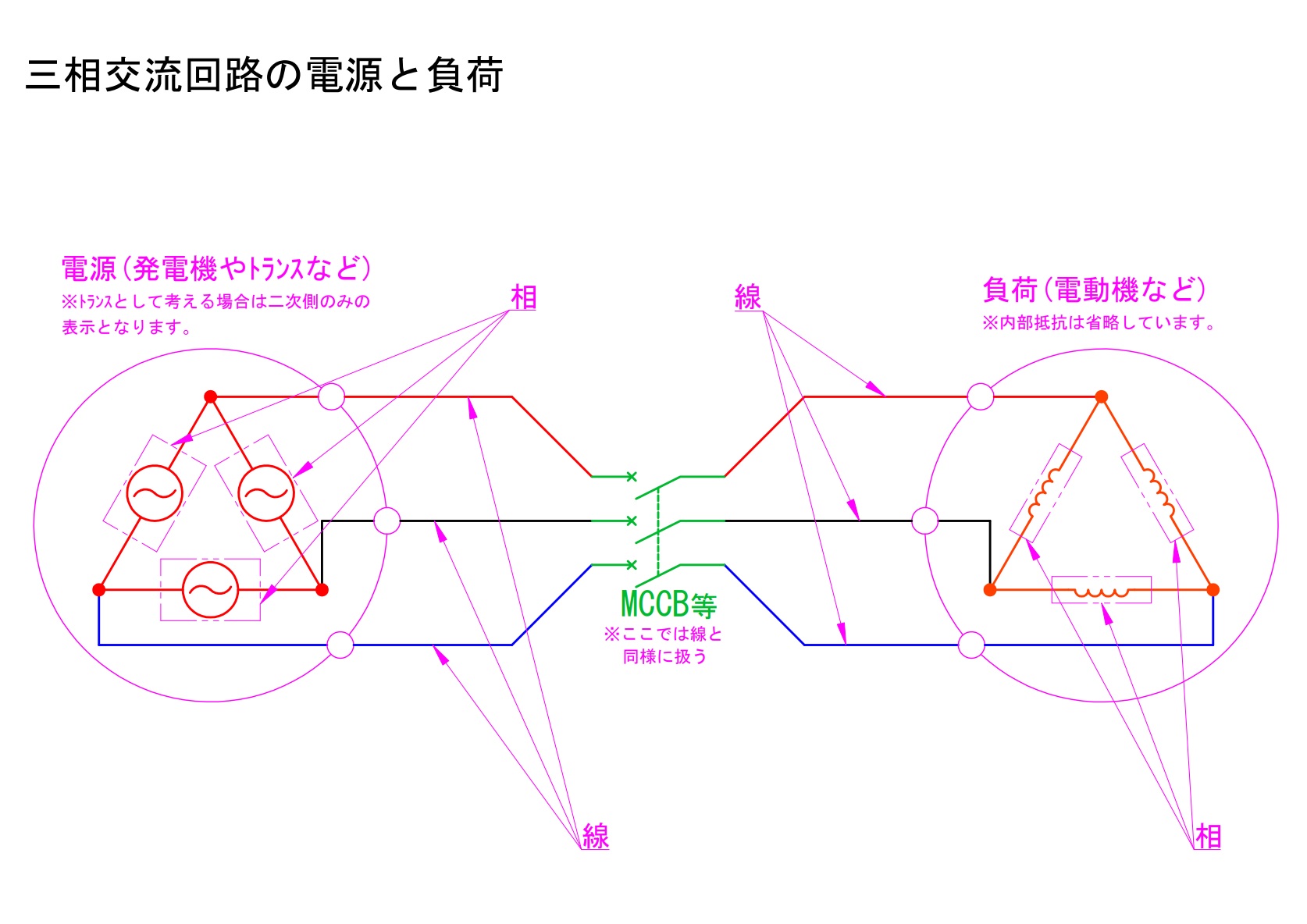
単相交流回路には無く三相交流回路に存在する概念が「相」と「線」という考え方であるということを前項に挙げましたがこれはどういう考え方なのでしょうか。まず、単相交流回路と三相交流回路は見た目でわかるくらい明確な違いがあります。以下の図は誘導電動機を駆動させるための単相交流と三相交流の主回路図です(単相誘導電動機では始動巻線などを省略し主巻線のみ表示しています)。
見た目から全く違いますよね。この図からでも見出にある「相」や「線」がどこの何を指すのか程度は説明できます。箇所としてはすでに図中に書き込んでいるものがそうです。図中の三角形の各辺に位置する電源やコイルが「相」であり、三角形の各頂点から外へ引き出されている線をそのまま「線」と表現しています。
単相交流回路では存在し得ないことが一目でわかりますね。また、同時に単相交流回路ではこのような「相」と「線」の概念が存在しない理由も図からわかります。
あえて言葉にするなら「相」は電源としてはたらくコイル部分、「線」は電源と負荷をつなぐ端子間の経路と表現して差支えないでしょう。単相交流回路にはこのように分ける境目が無いですね。単相交流回路では「相」でのエネルギー発生は「線」で伝達されるそれと同じです。
それではこの「相」と「線」、三相交流回路でどのように扱うべきなのかをみていきます。
1)スター結線とデルタ結線
「相」と「線」の違いを正しく理解していくために先ず必要となる知識が「スター結線」と「デルタ結線」という結線方法です。図面などではスター結線を「Y結線」、デルタ結線を「Δ結線」と書き表していることもしばしばあります。またスター結線を「星形結線」、デルタ結線を「三角結線」という場合もあります。さらにスター結線は「Y」を逆さまにした「⅄(ターンドY)」という記号を使用することもあります。
ここでは「Y結線」「Δ結線」の表記を使用します。
言葉の説明が長くなりましたが以下の図が電源と負荷におけるY結線とΔ結線になります。電源はコイル記号、負荷は抵抗器の記号を使用しています。
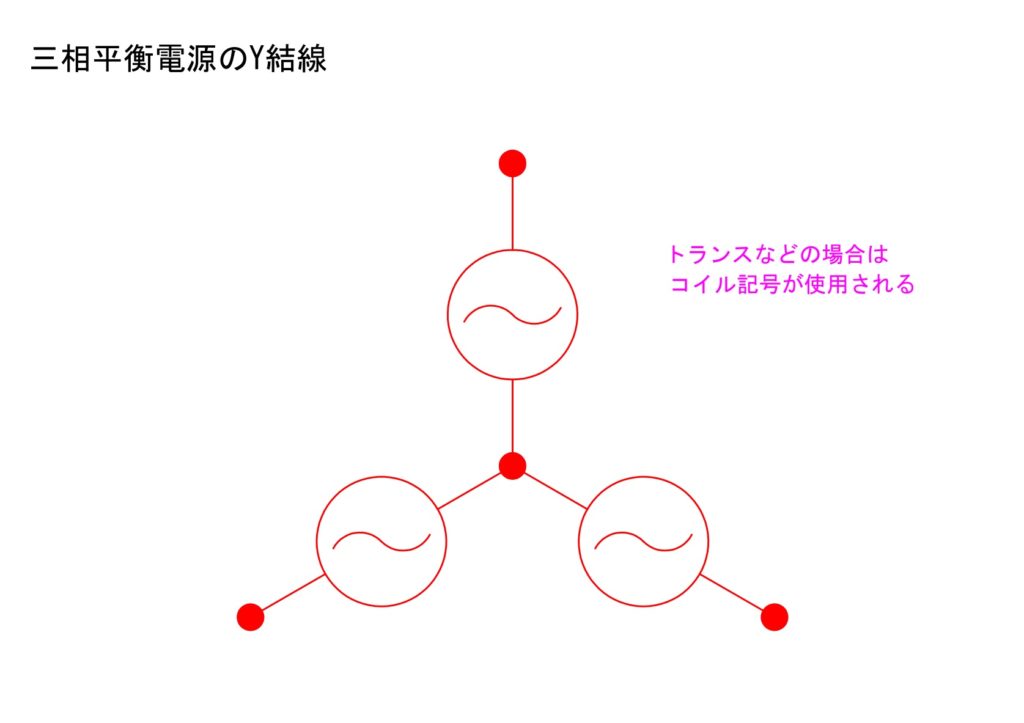
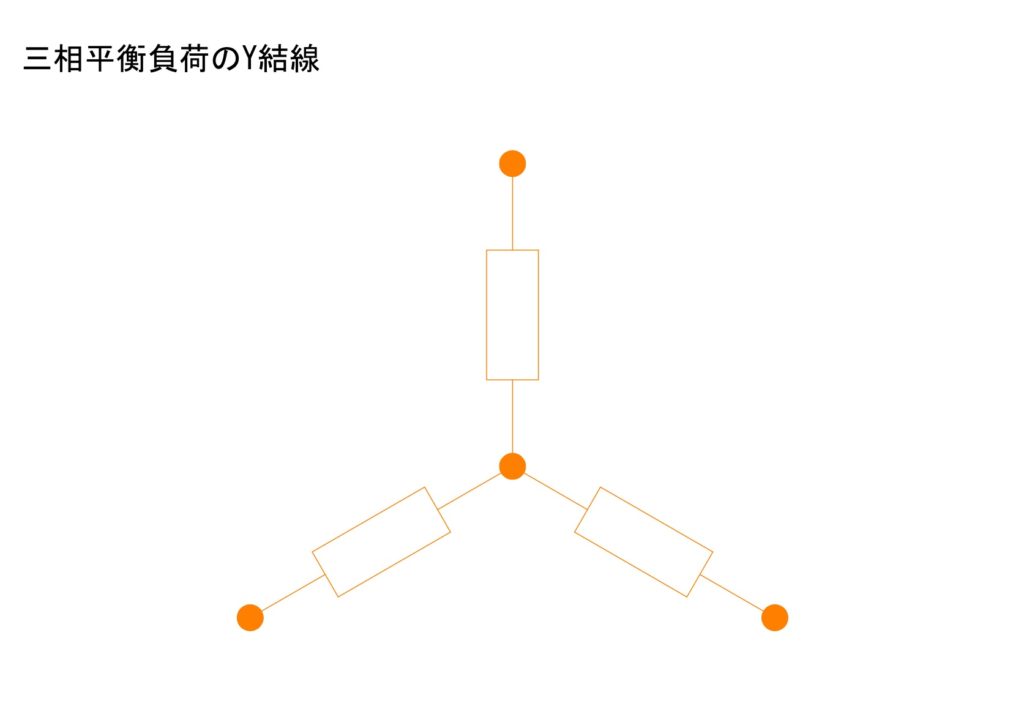
a.Y結線
電源も負荷も三つのコイルや抵抗がひとまとめに接続されている一点がありますね。見た目に⅄やYの形になっています。
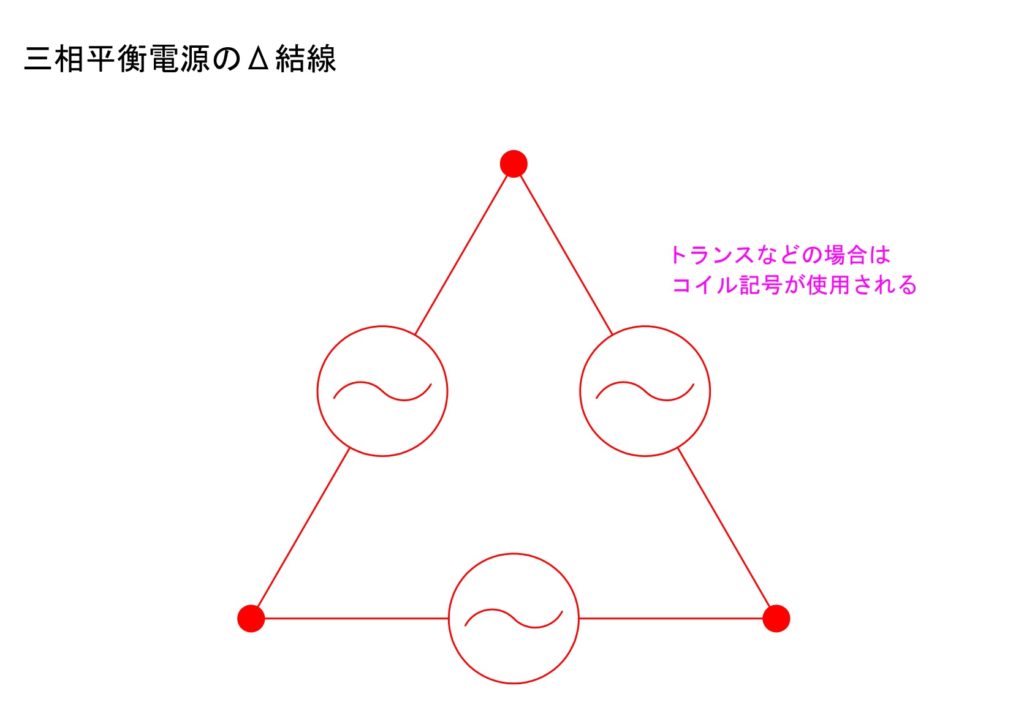
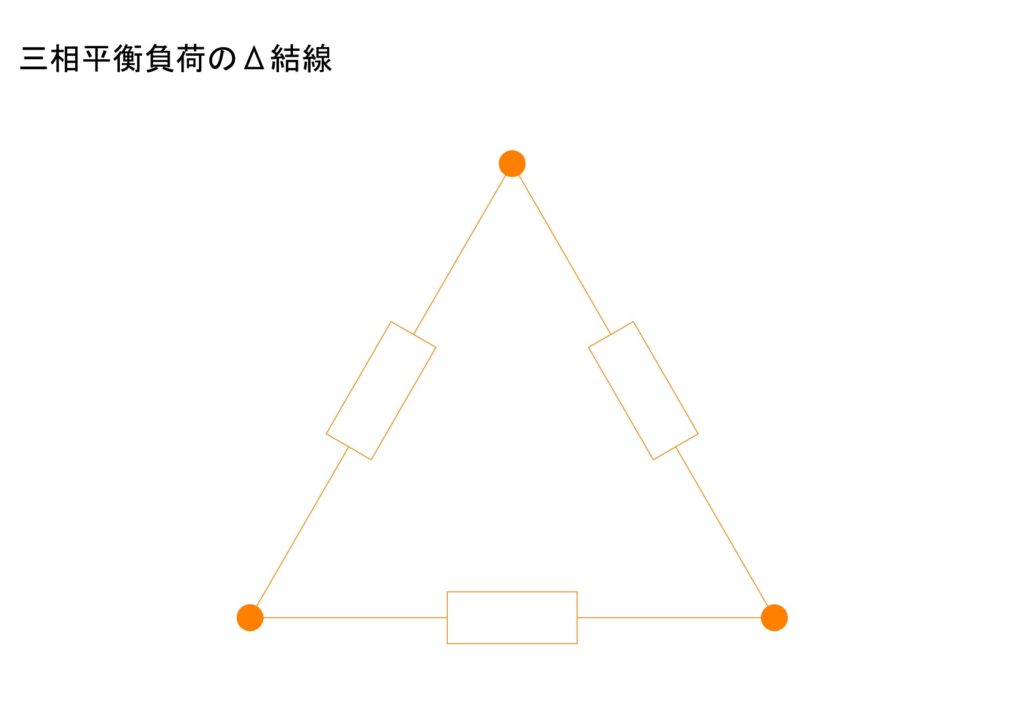
b.Δ結線
電源も負荷も三角形を形成するように接続されています。
2)接続の組み合わせは4種類
上記で電源と負荷に関する各々2種類の接続方法を図で説明しました。ということは電源2種類×負荷2種類で計4種類の接続方法が存在するということになります。以下にそのすべて接続の状態を図にしています。
いずれの場合の結線方法や組み合わせでも「相」と「線」の範囲に変化はありません。
3.「平衡」が前提
三相交流回路の「相」と「線」を理解するうえでもう一つおさえておかなければならない前提があります。それが「平衡」という考え方です。三相交流の電源が実用上有効にエネルギーとして作用するには多くの場合で電源も負荷も「平衡している」必要があります。
「平衡」とはバランスしている状態のことをいいます。
平衡していない状態としては、例えばY,Δのどのような結線であっても各相の電圧がここは100[V]それは200[V]あちらは500[V]となっており負荷もこれは10[Ω]それは100[Ω]あちらは0.5[Ω]などとなっていては電動機やヒーターなどで狙った効果が得にくいですし危険も伴います。というより計算が複雑になるだけであり、実用上わざわざそうする意味がありませんしデメリットしか生みません。
一部の炉などでは機械上負荷を平衡させられないものもある場合がを見てきましたが、結果各線電流がバランスしていませんでした。このアンバランスが大きくなると電源品質にかかわってきます。また省エネ法ではこのようなアンバランスは良しとしませんので三相交流回路は本来平衡状態であるべきです。
三相が平衡した電源を三相平衡電源といいます。そして三相が平衡した負荷のことを三相平衡負荷といいます。
4.「相」と「線」での電圧,電流
三相交流回路では電圧は電圧でも「相」に印加の「相電圧」か「線間」に印加の「線間電圧」かは別物として扱う必要があります。また、電流でも同じで「相」に生じる「相電流」か「線」に生じる「線電流」かも別物として扱うことになります。
ここで電圧について「線間電圧」だけ「間」という字が使われていますがこれにもちゃんと意味があり、電圧は同一の線上で測ってもほぼ0[V]であり、例えば無理やり線電圧として一本の電線のあちらとこちらで計測することに通常あまり意味がありません(電線の抵抗などに着眼する場合は別ですが)。「線間電圧」という言い回しに関してはあくまで線や端子をまたぐことで意味のある計測となることが起因していると考えられます。
では、各接続パターンにおける三相交流回路での「相」と「線」の関係をみていきます。ここには一定の現象であり約束事となるものがあります。この現象がとても大事であり試験上も実務上もこの理解が必要となってきます。あくまで三相平衡回路での話であることを前提としています。
この後の図に出てくる記号については以下のとおりとします。書籍では「´(ダッシュ)記号」の付加記号や大文字小文字や添え字など様々ですが、ここでは原則的に「相」という意味の「Phase」の頭文字から「P」を、「線」という意味の「Line」の頭文字から「ℓ」を添え字として用いています。また同じ「相」でも電源側を「Electromotive」の「E」を、負荷側を「Load」の「L」を添え字として使用しています。
【電圧】
電源側相電圧:E[V]
負荷側相電圧:VP[V]
線間電圧:Vℓ[V]
【電流】
電源側相電流:IEP[A]
負荷側相電流:ILP[A]
線電流:Iℓ[A]
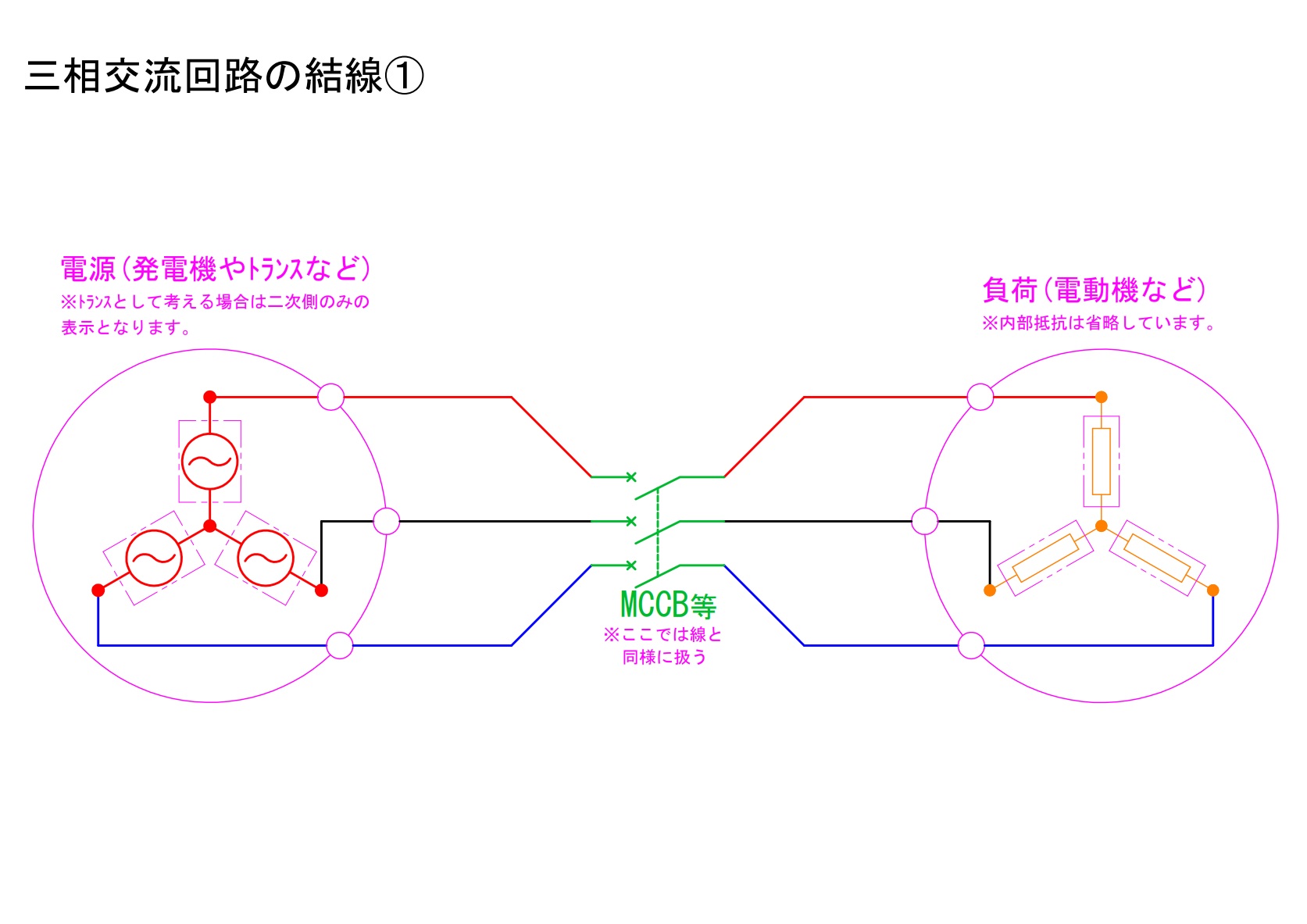
1)電源がY結線で負荷もY結線の場合
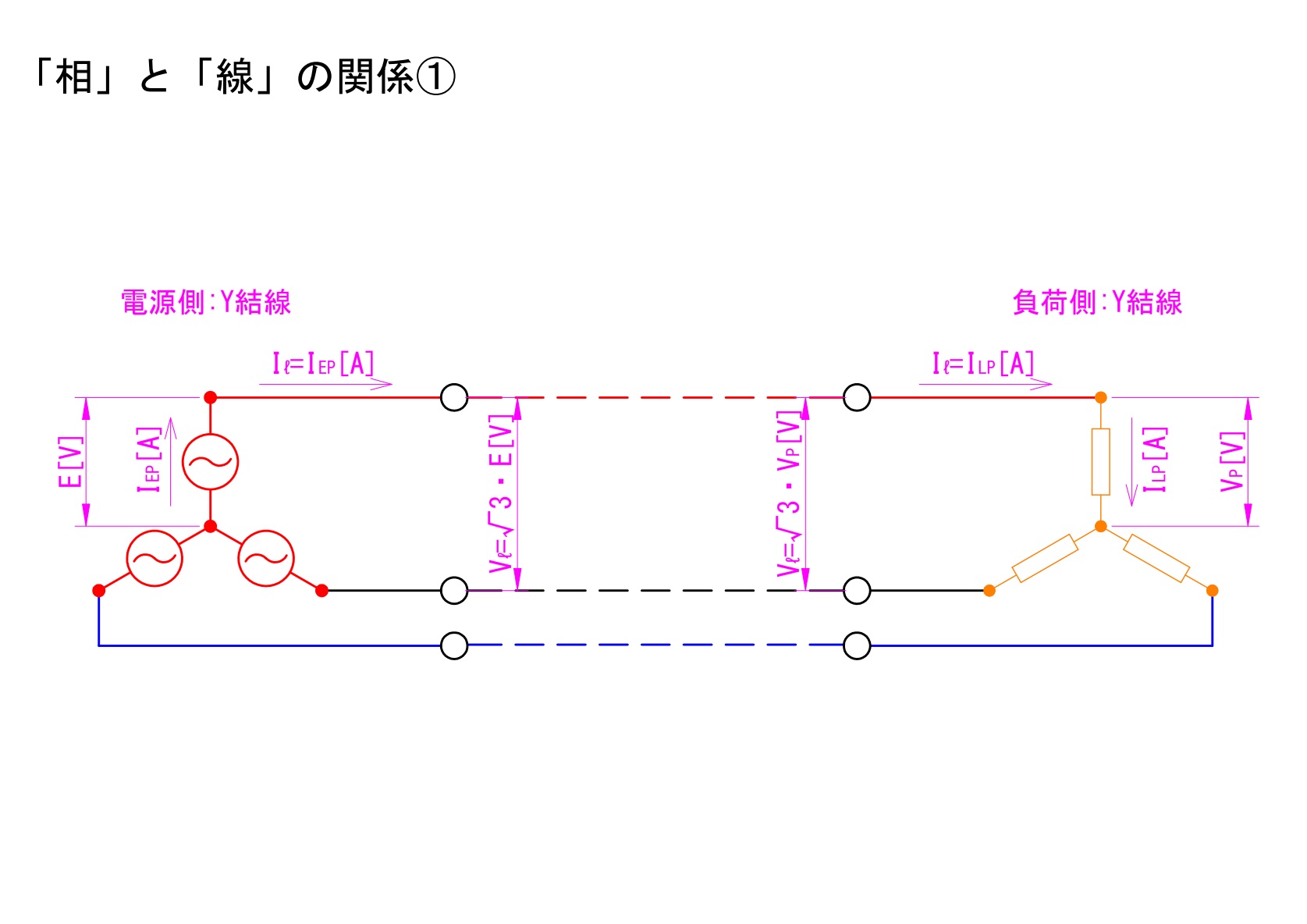
電源がY結線で負荷もY結線の場合における、「相」と「線」の関係について説明します。
電源側:線間電圧が相電圧の√3倍。線電流は相電流と等しい。
負荷側:線間電圧が相電圧の√3倍。線電流は相電流と等しい。
上記を説明したものが以下の図です。
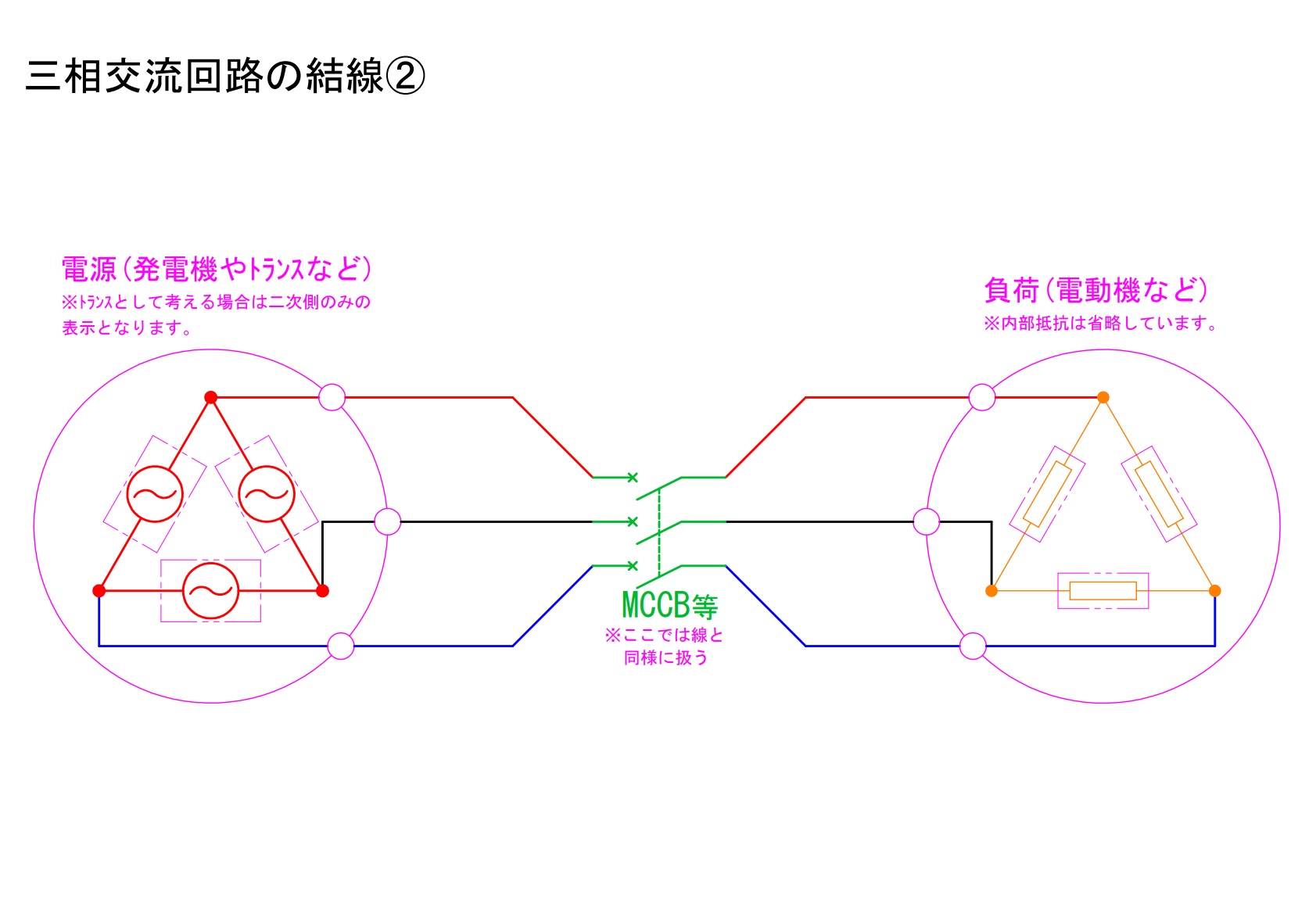
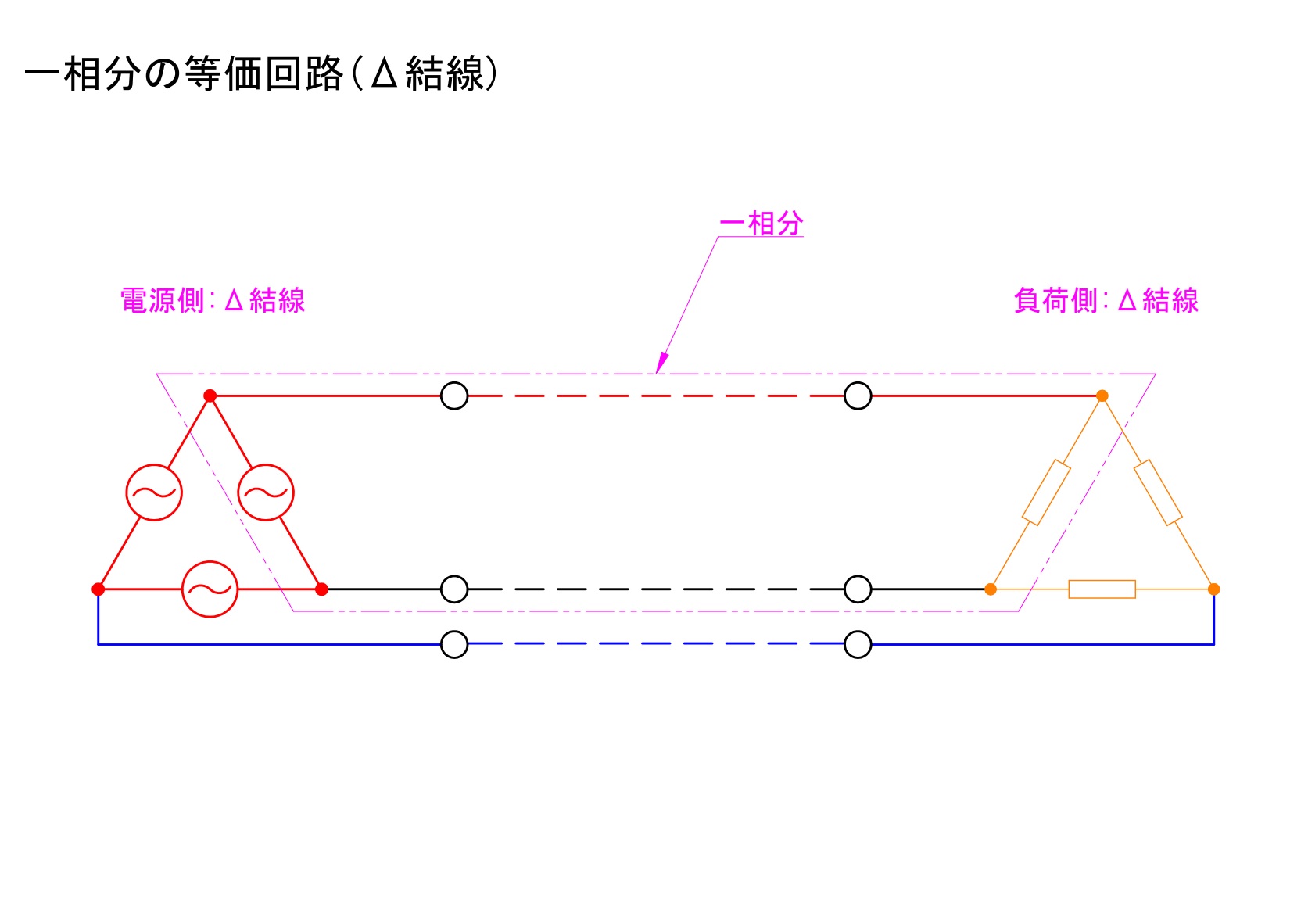
2)電源がΔ結線で負荷もΔ結線の場合
電源がΔ結線で負荷もΔ結線の場合における、「相」と「線」の関係について説明します。
電源側:線間電圧は相電圧と等しい。線電流は相電流の√3倍。
負荷側:線間電圧は相電圧と等しい。線電流は相電流の√3倍。
上記を説明したものが以下の図です。
3)電源がY結線で負荷はΔ結線の場合
電源がY結線で負荷はΔ結線の場合における、「相」と「線」の関係について説明します。
電源側:線間電圧は相電圧の√3倍。線間電流は相電流と等しい。
負荷側:線間電圧は相電圧と等しい。線電流は相電流の√3倍。
上記を説明したものが以下の図です。
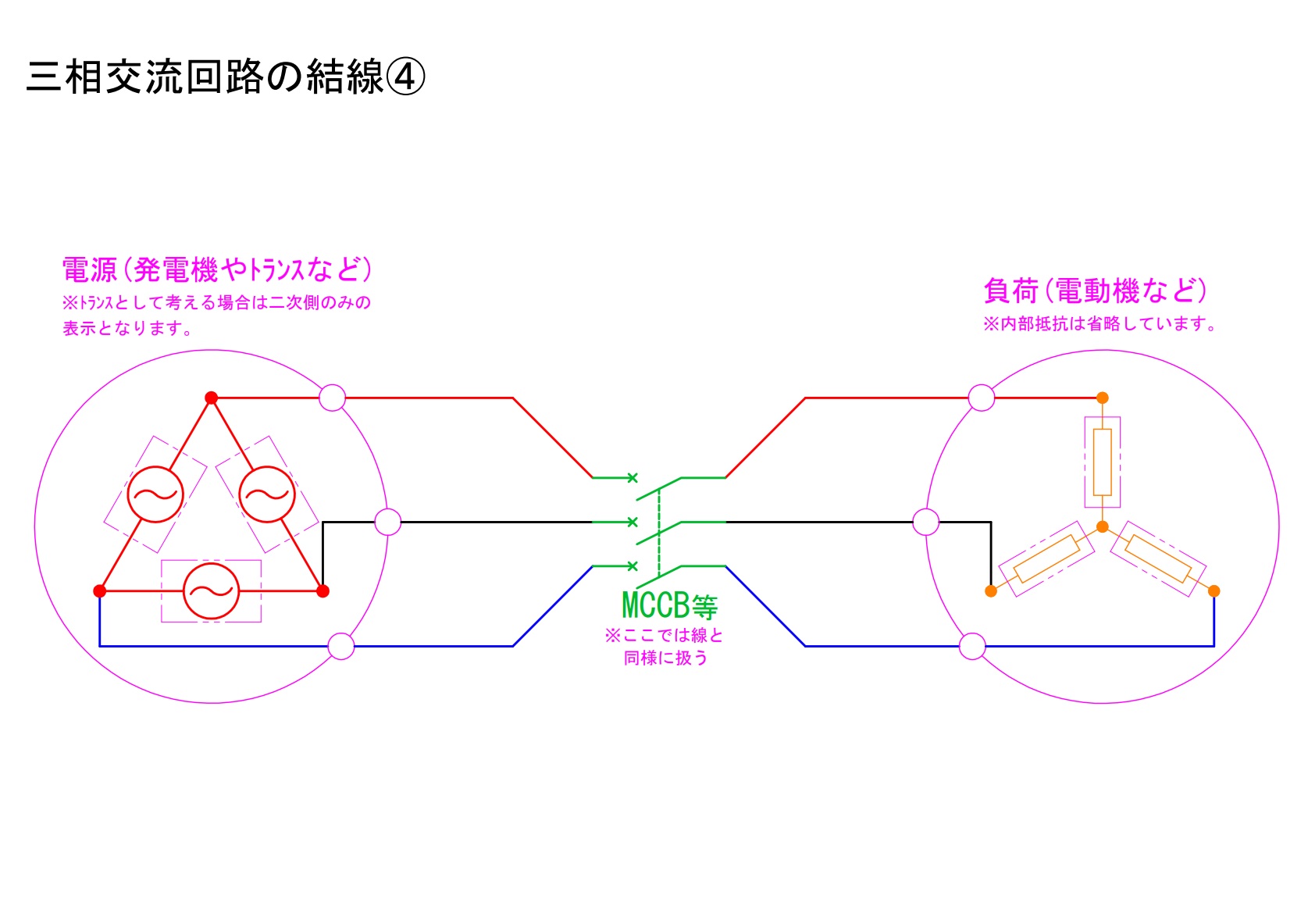
4)電源がΔ結線で負荷はY結線の場合
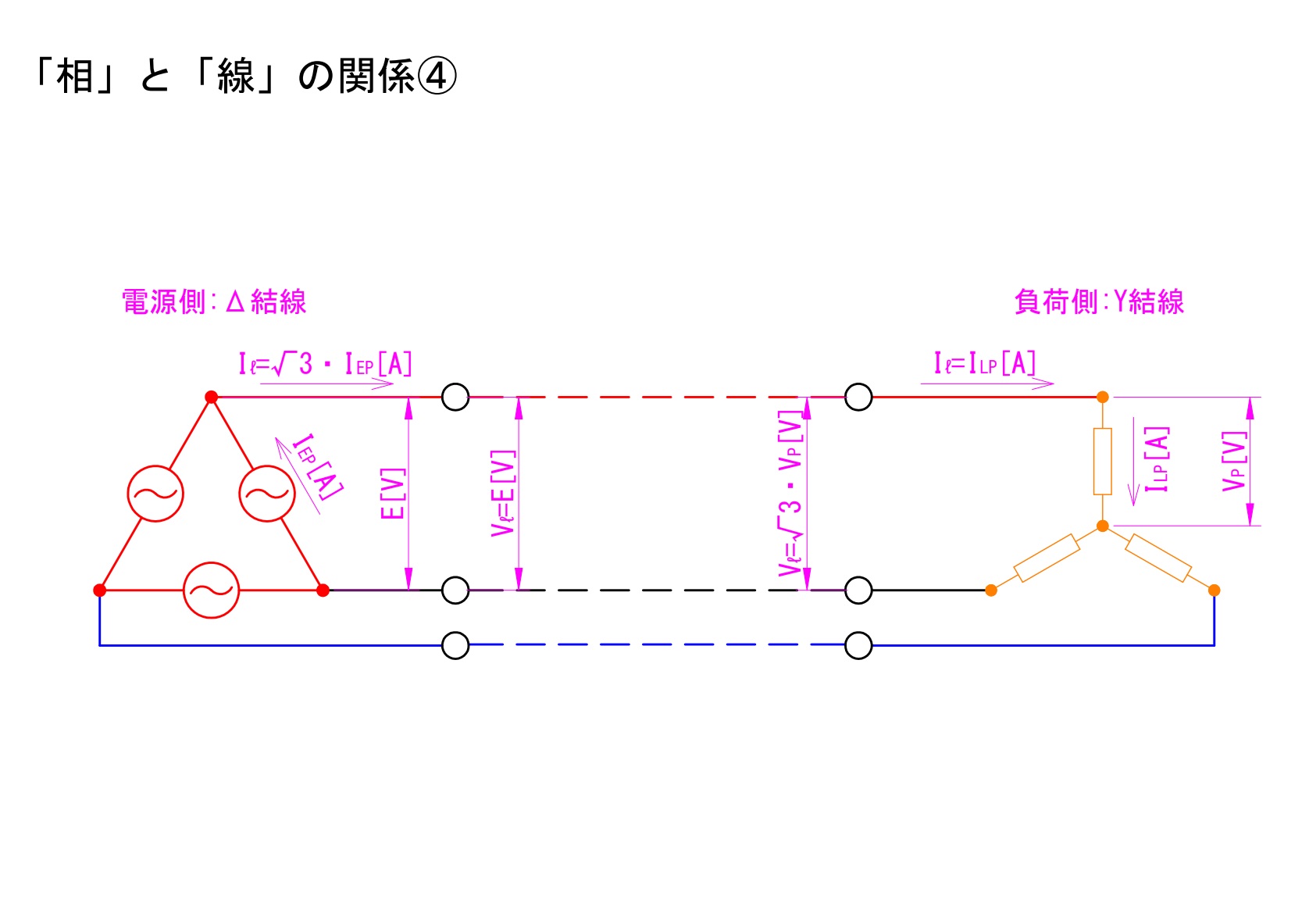
電源がΔ結線で負荷はY結線の場合における、「相」と「線」の関係について説明します。
電源側:線間電圧は相電圧と等しい。線電流は相電流の√3倍。
負荷側:線間電圧は相電圧の√3倍。線電流は相電流と等しい。
上記を説明したものが以下の図です。
5.一相分の等価回路へ変換
前の項目で各接続パターンにおける「相」と「線」の関係について説明しました。非常にややこしく、頭の中がごちゃごちゃになってしまいそうですね。
「相」と「線」の電圧,電流については理解できたとしてもこれらをどのように活用すれば三相交流回路での様々な計算に取り込めるのでしょうか。これについて以下に説明していきます。
結論からいうと、「一相分に変換する」ということになります。先のY結線やΔ結線を双方同じ形状の結線にみたてたうえで「相」と「線」での関係を適用することで一相分の回路へ変換して計算することができます。具体的には前項の「1)」や「2)」のように電源側と負荷側の結線を同じにするということです。そうすることで単相交流回路と同じように計算することが可能となります。
このとき必要となるのが負荷のY-Δ変換に関してです。電源側の場合「相」として扱うか、「線」として扱うかは対象となる機器に応じて決定しますが、一相分の回路変換により電流などの計算をするには負荷側の結線状態を電源側に合わせる必要がでてきます。その方が考えやすく計算しやすいからです。ということは電源の変換状況に応じて負荷側を自由に変換できる必要があります。
そして一相分の等価回路から三相回路へ戻す際に再び「4.」で説明した「相」と「線」の関係で整理するということになります。
1)負荷のY-Δ及びΔ-Y変換
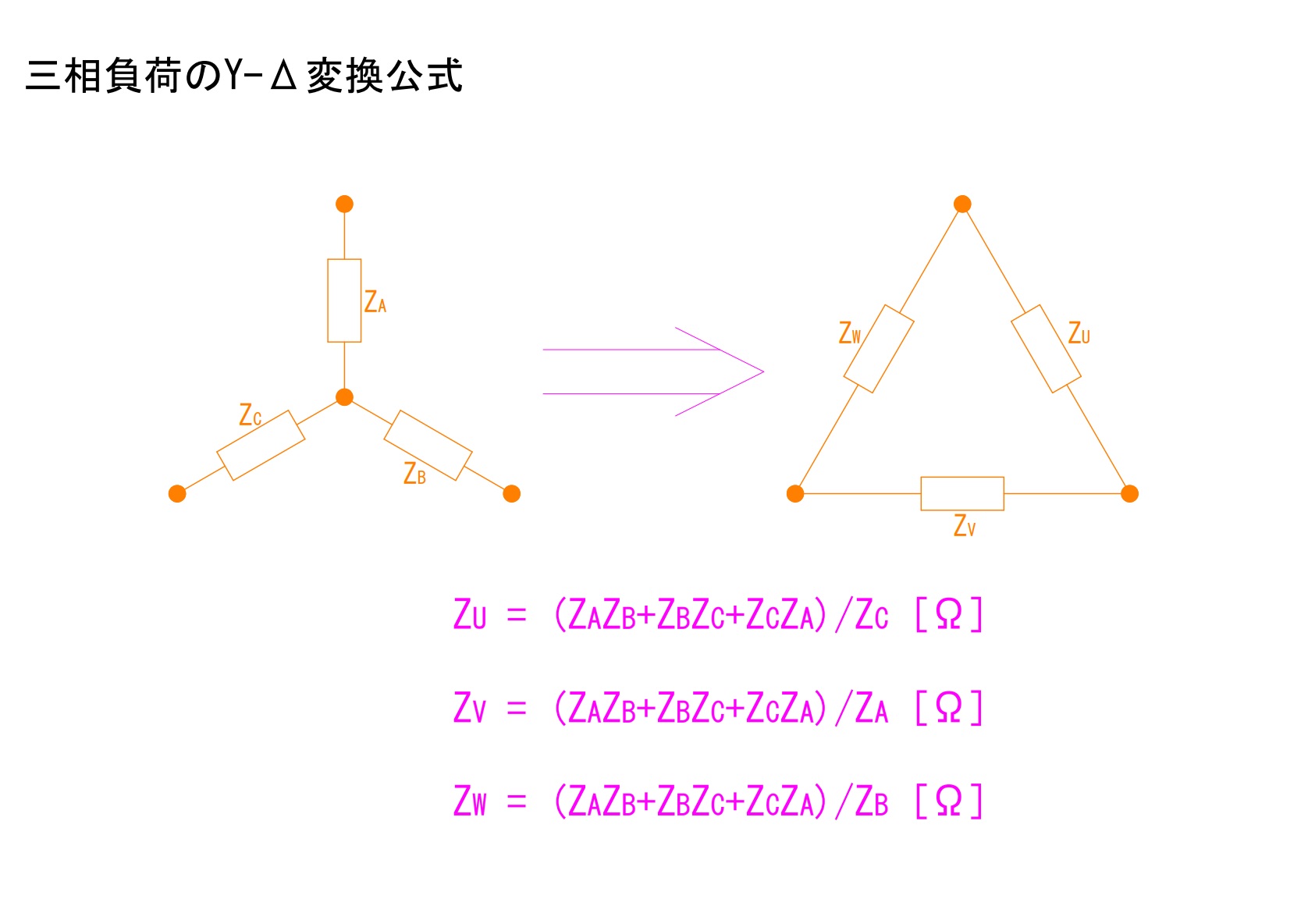
負荷のY-Δ変換やΔ-Y変換では以下の公式を用います。三相平衡負荷の場合はこの計算がすべて同じ大きさの負荷に対してのものになるので簡略化が可能となります。
以下に変換の公式を記載しています。
なお、以下で「Z[Ω]」の記号を使用していますが、これは電気抵抗を表す「R[Ω]」に対して負荷がコイル成分やコンデンサ成分を含む場合の表記となります。
この公式に則り三相平衡負荷を変換する場合、Y-ΔにおいてはZA,ZB,ZCが各々等しい状態です。そして、Δ-YにおいてはZU,ZV,ZWが各々等しい状態となります。仮に以下のように仮定すると三相平衡負荷における双方の変換はより単純化されます。
【Y-Δ変換においてZA=ZB=ZC=ZYの場合】
変換前をZY[Ω]、変換後をZΔ[Ω]とおく。
$Z_U=Z_V=Z_W=Z_Δ=\frac{3{Z_Y}^2}{Z_Y}=3Z_Y$ [Ω]
【Δ-Y変換においてZU=ZV=ZW=ZΔの場合】
変換前をZΔ[Ω]、変換後をZY[Ω]とおく。
$Z_A=Z_B=Z_C=Z_Y=\frac{{Z_Δ}^2}{3Z_Δ}=\frac{Z_Δ}{3}$ [Ω]
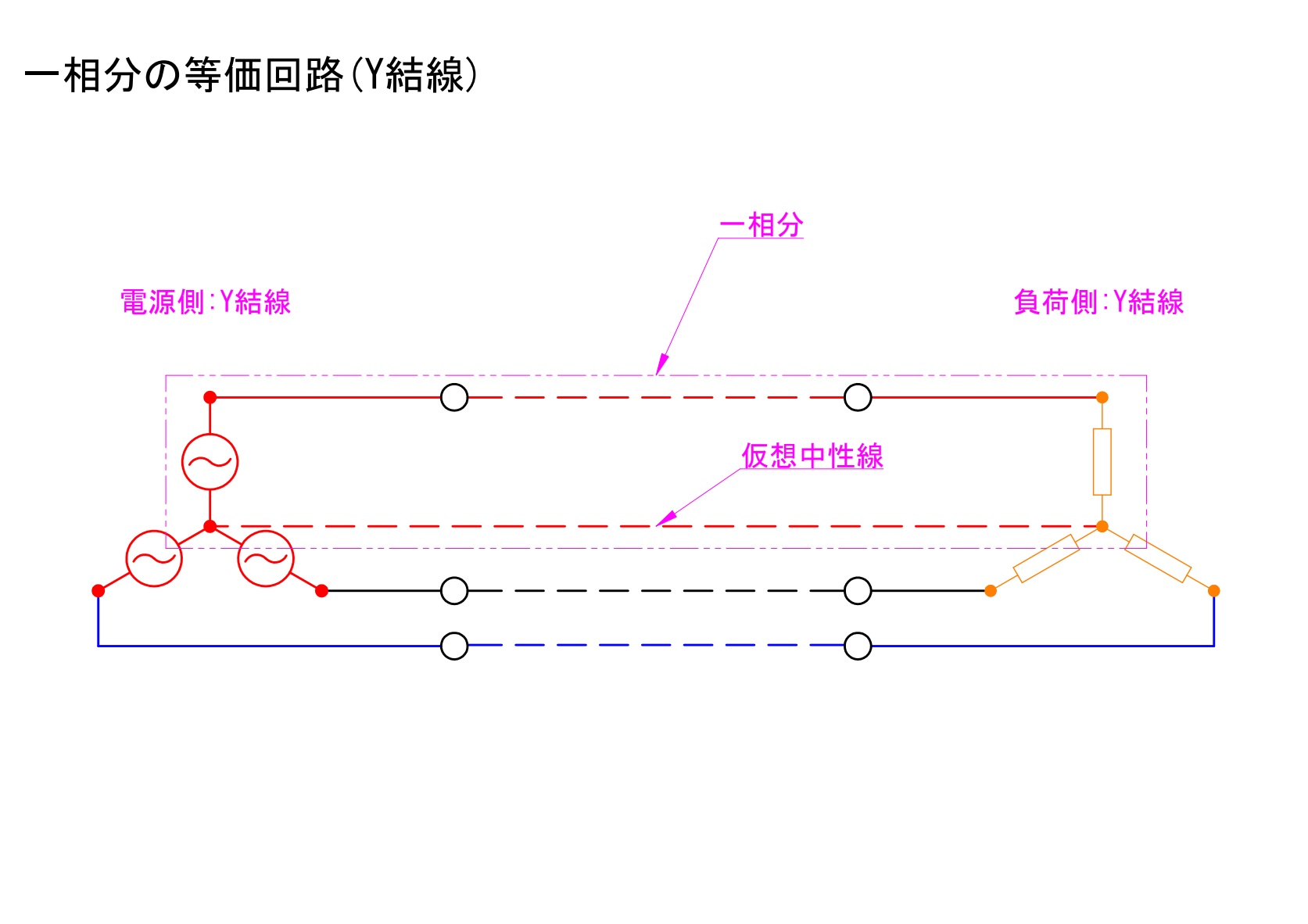
2)一相分の等価回路
電源と負荷の結線状態を合わせた状態であればこれらを各々1:1で取り出して考えることが可能となります。そうすると、前述のとおり、単相交流回路として計算することが可能となります。留意点としては、Y結線での一相分の等価回路変換においては帰線としての仮想中性線を考慮しなければならないということがあります。
計算自体は負荷が純抵抗ならばオームの法則にそのまま当てはめる形となります。負荷にコイルやコンデンサを含む場合は力率の考え方を適用します。
そうして計算した結果は再び該当の結線状態に戻す際に必要に応じて「4.」の関係にあるとおりに換算することで完了します。
6.関係性の理解のうえで
ここまで三相交流回路における「相」と「線」の関係とその計算方法について解説してきました。ここでの知識の必要性は、各電気試験においては言わずもがなであり、実務においても変圧器選定や電動機始動時の設計などに大きく響いてきます。
また、力率や計測について理解を深めるためにも必須の知識となります。是非、ゆっくりと理解を深め三相交流についてマスターしていきたいものです。