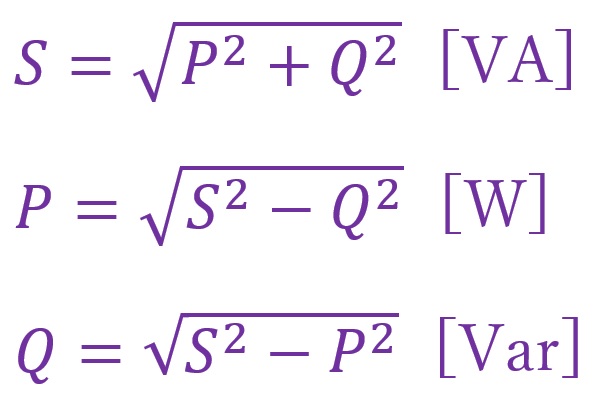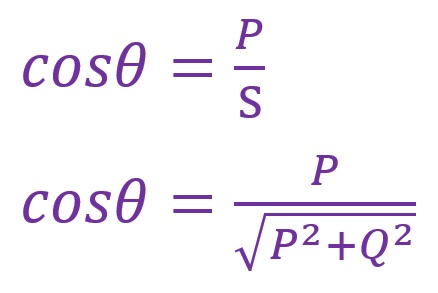1 .「力率」という概念
電気について学び始めて交流回路の項目に入っていくと、ほどなくして「力率」という言葉を見かけるようになります。この「力率」っていったいどのようなものなのでしょうか。学習中にいきなり出てきてその理解に困ったという方へ向けて初歩的ではありますが解説をします。
1)「有効」利用できたか「無効」であったか
「力率」について端的にいうと、電力を「有効に利用(消費)できたかどうかの比率」であるといえます。では電力を「有効」に利用するということはどのようなことなのでしょうか。また「無効」である状態とはどのようなことをいうのでしょうか。
ここでいう電力の有効利用とは、電力会社などから供給された電力を、熱などのエネルギーとして消費できた分を指します。これを「有効電力」といいます。そして無効である状態とは電力使用の回路内で蓄積と放電を繰り返すのみとなり、目的とするエネルギーとして利用されない分を指します。これを「無効電力」といいます。
このエネルギーとして利用されない無効である電力も回路を動作させるために必要である場合、有効に利用する分とは別途供給される必要があり、電力会社などはそれを含めたエネルギーを送り出すこととなります。この有効電力も無効電力も含めた全供給電力を「皮相電力」といいます。
ちなみに各々単位が異なりますので、その記号とともに以下に記載しておきます。
【有効電力】:P[W] (単位の読みは「ワット」)
【無効電力】:Q[Var] (単位の読みは「バール」)
【皮相電力】:S[VA] (単位の読みは「ボルトアンペア(ブイエー)」)
2)「皮相電力=有効電力」が望ましい
もちろん電力は供給された分をすべて有効電力として使用することが望ましいです。
これは電力供給側から見た場合においては、有効に消費されない無効電力分も加味した供給を強いられる必要がなくなることを意味しています。また、消費側から見れば有効に消費していないエネルギーの対価まで用意する必要から逃れられるということを意味しています。
電力消費においては需要供給ともに「皮相電力=有効電力」であることが望ましいのですね。では、この有効電力と無効電力とを切り分ける条件とはいったい何になるのでしょうか。どうすれば有効電力として消費でき、どうすれば無効電力になってしまうのでしょうか。
以降、電気エネルギーを有効に消費する条件と無効である場合の条件について解説します。
2.「有効電力」と「無効電力」を決めるもの
力率とはどういったものかについて説明しましたが、ではこの有効電力や無効電力といったエネルギー利用の状態は何によって決定されるかについて説明します。
1)回路素子で決定される
ある電気回路で供給された電力を有効に消費できるか否かはその回路を構成する素子によって決定されます。回路素子と一言にいっても、よく耳にするダイオードやトランジスタまたサイリスタやICなど様々ですが、ここでとり上げられる素子は「電気回路」の構成素子という意味で「抵抗」「コイル」「コンデンサ」のことになります。
先にあげたダイオードなどの素子は「能動素子」といわれ、電子回路に組み込まれて増幅や整流という作用を生み出します。対して「抵抗」「コイル」「コンデンサ」は「受動素子」といわれ、能動素子のような性質はありません。文字通り受け身な反応を示すものです。抵抗では電圧降下を、コイルでは反発の、コンデンサでは蓄積の反応を各々示す素子となります。
この三つの素子が電力を有効に消費できるかどうかの決め手となります。
2)有効利用できるのは「抵抗」のみ
では「抵抗」「コイル」「コンデンサ」がどうあれば電力を有効に利用できるかについて説明します。一言で終わってしまうのですが電力を有効に消費できるのは抵抗のみです。
「えっ!?」と思われた方も多いと思います。電動機(モーター)や電源用のアダプターやインバーターなどコイルやコンデンサを使った機器なんていくらでもあるのにそれらすべては電力の消費上無効であり、かつ抵抗のみが有効消費しているなんてちょっと感覚が追いつきませんよね。
簡単にいうとコイルなどは特に顕著ですが、コイルにも抵抗成分というものが存在し有効に消費できる部分と無効である部分とに分けられます。しかし、あくまで電力を有効に消費するのは抵抗成分です。
3.「力率」の計算
ここまで力率が何に依存するのかについて説明してきました。では、次にその比率は如何ほどかについて、計算のしかたを説明していきます。まず力率は皮相電力に対する有効電力の比率となります。ここまで聞くと「じゃああとは有効電力を皮相電力で割れば計算できるでしょ。」と考えるのが普通ですね。はい、そうです。合ってます。
しかしこの「皮相電力」、一般に使われる比率計算上の100%とは少し違う概念をもっています。ここがこの力率計算のややこしいところなのです。
数式の表示がうまくいかない場合のために、画像も用意しています。ご活用ください。
1)一般的な比率計算
まずは、一般的な比率計算についておさらいしておきます。
例えばアンケートで「あなたは勉強がすきですか?」という質問があったとします。これを200[人]に尋ねたところ、その回答で「はい」と答えた人が40[人]、「いいえ」と答えた人が160[人]だったとします。
この場合「はい」の回答割合は40/200=0.2となり、百分率ならこれに100をかけて20[%]という結果になります。同様に 「いいえ」の回答割合は160/200=0.8となり、百分率なら80[%]という結果になります。そしてこの20[%]と80[%]を足し合わせると100[%]になります。
これが一般的によく見る比率計算です。
ですが、力率では上記ように「はい」の回答と「いいえ」の回答を足したら100[%]なるという計算が成り立たないのです。本当にややこしいですね。では力率ではどのような計算になるのかというと「三平方の定理」別名「ピタゴラスの定理」を用いることになります。
2)三平方の定理
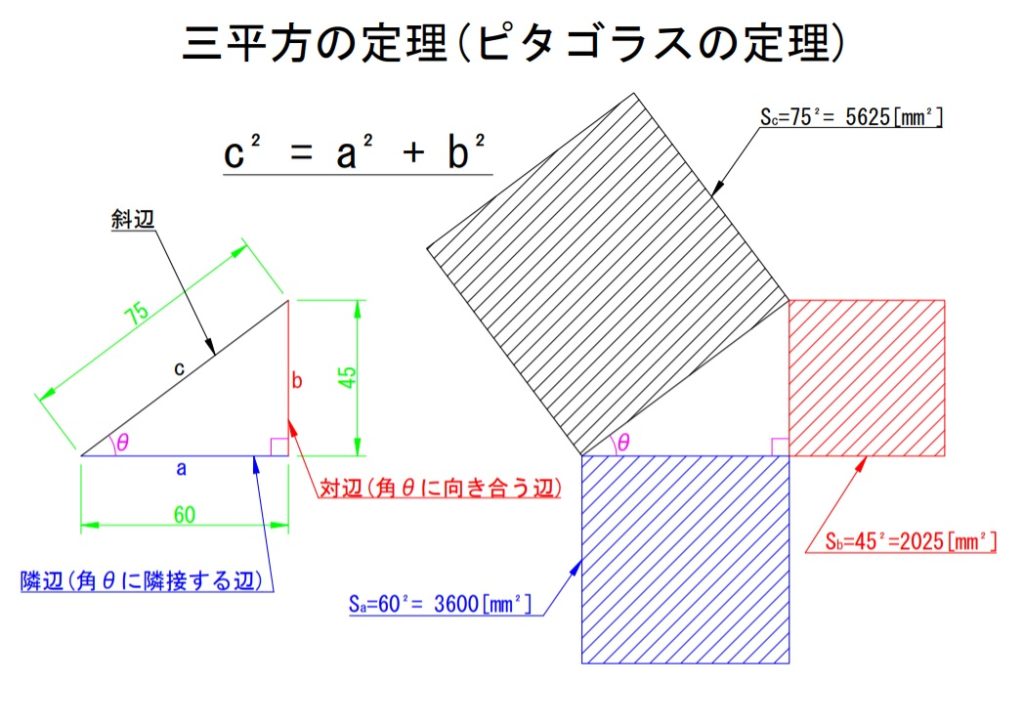
三平方の定理とは「直角三角形において斜辺を2乗したものは、隣辺(底辺)を2乗したものと対辺を2乗したものの和と等しい」という性質のことをいいます。これまた言葉だけではわかりにくいですね。以下に図で説明しています。
例として「a=60[mm]」「b=45[mm]」「c=75[mm]」とします。
「2乗」ということは正方形の面積の計算方法であり、三平方の定理では隣辺,対辺各々の辺で形成される正方形の面積の和は斜辺で形成される正方形の面積に等しくなるということをいっています。
これが、力率計算の肝となります。
3)「皮相電力」「有効電力」「無効電力」
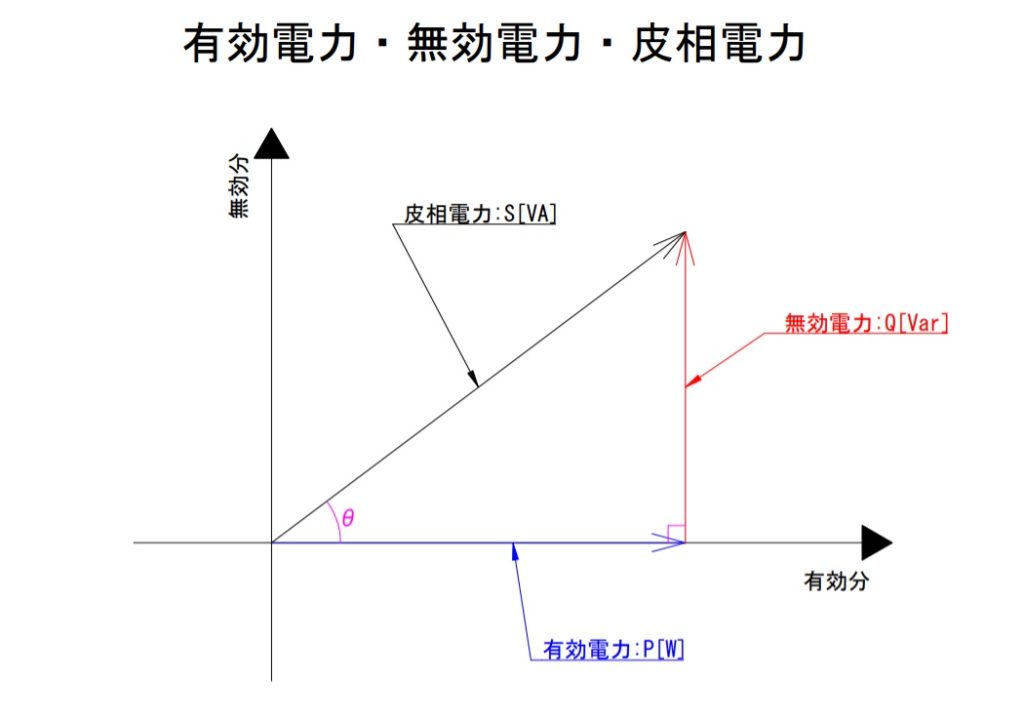
では、三平方の定理で説明される各辺と各電力成分はどれがどれに位置するのでしょうか。それを図で以下に記載します。
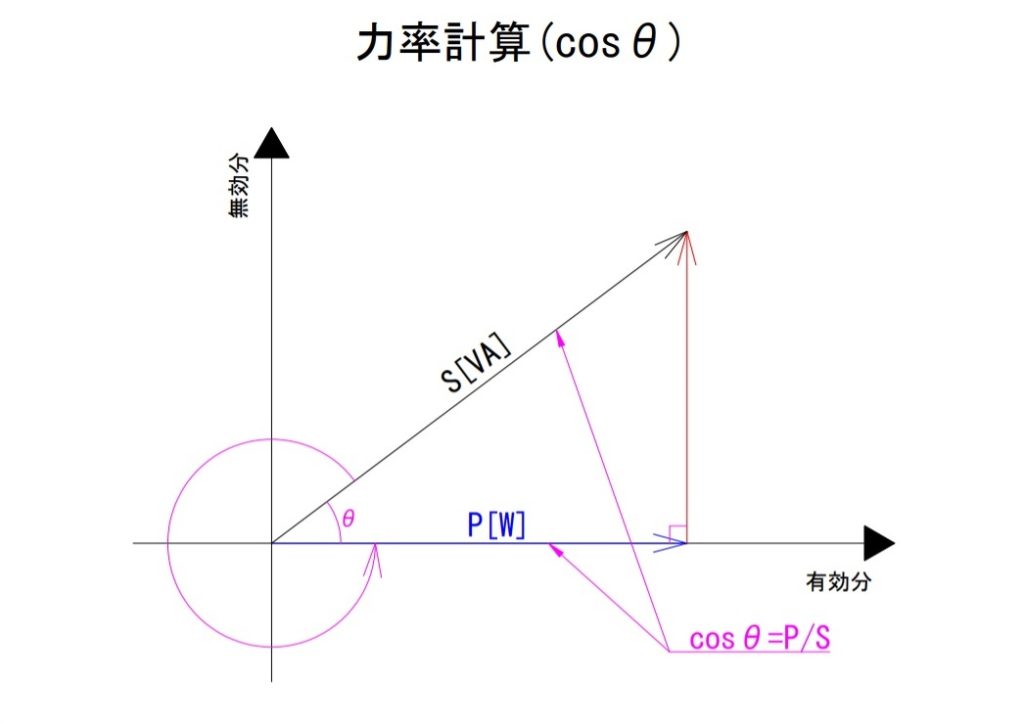
力率計算においては、横軸つまり隣辺を有効電力とし、縦軸つまり対辺を無効電力とし、斜辺を皮相電力としています。これが力率計算における各電力成分の関係となります。
改めて言葉で説明するならば、「有効電力の2乗と無効電力の2乗の和は皮相電力の2乗に等しい」ということです。式に表すと以下のとおりになります。
$S^2=P^2+Q^2$
書き換えると以下になります。
$S=\sqrt{P^2+Q^2}$ [VA]
$P=\sqrt{S^2-Q^2}$ [W]
$Q=\sqrt{S^2-P^2}$ [Var]
4)皮相電力に対する有効電力の比
上記で皮相電力と有効電力と無効電力の関係を説明しましたがこれらを踏まえることでやっと力率を計上することが可能となります。先に説明したとおり、力率は皮相電力に対する有効電力の比ですので単純な分数で計算できますが、あくまで各電力成分は三平方の定理から導かれるものであることを忘れないように注意してください。
ちなみに力率は「cosθ(コサインシータ)」で表されます。これは数学の三角関数の表記と全く同じです。測定機器などでは「PF[%]」で表されることもあります。[%]がつく場合は一般的な比率計算と同様に百分率表記となります。以下力率の計算式です。
$\cos\theta=\frac{P}{S}$
$\cos\theta=\frac{P}{\sqrt{P^2+Q^2}}$
5)遅れ力率と進み力率
力率には「遅れ」と「進み」があります。英語表記では「LAG」と「LEAD」となります。直角三角形の対辺つまり無効電力成分が隣辺に対して(紙面の)下に伸びている場合は「遅れ力率」といいます。「位相が遅れている」ともいいます。また無効電力成分が隣辺に対して(紙面の)上に伸びている場合は「進み力率」となります。「位相が進んでいる」ともいいます。遅れや進みによる差分を「位相差」といいます。
「位相差」については、有効電力を基準としたときの皮相電力の時間的なズレと認識してください。
そして力率が遅れとなるか進みとなるか、はたまた遅れも進みも無しになるかについてはコイルとコンデンサの有無およびそのバランスにより決定します。
4.「遅れ」「進み」の要因
上記で力率の遅れと進みについて述べましたが、これにはコイルとコンデンサが関係しているということでした。まず「遅れ」や「進み」とは何に対して遅れているのか、進んでいるのかを把握する必要があります。
結論からいうとこの「遅れ」や「進み」は印加された電圧に対して電流が遅れているのか進んでいるのかを言っています。抵抗やコイル,コンデンサを電源と接続し電圧を印加した直後、素子の一次側二次側間で電位差が生じた後に遅れて電流が生じる場合これを遅れ力率と表現し、電圧を印加した直後、素子一次側二次側間で電位差が生じる前に先行して電流が生じる場合これを進み力率と表現します。
感覚的につかみ取るのが難しい現象ですが今はそうであることだけ掴んでいただければ良いです。
そして抵抗を含むコイルとコンデンサで構成されている回路を「RLC回路」とよびます。
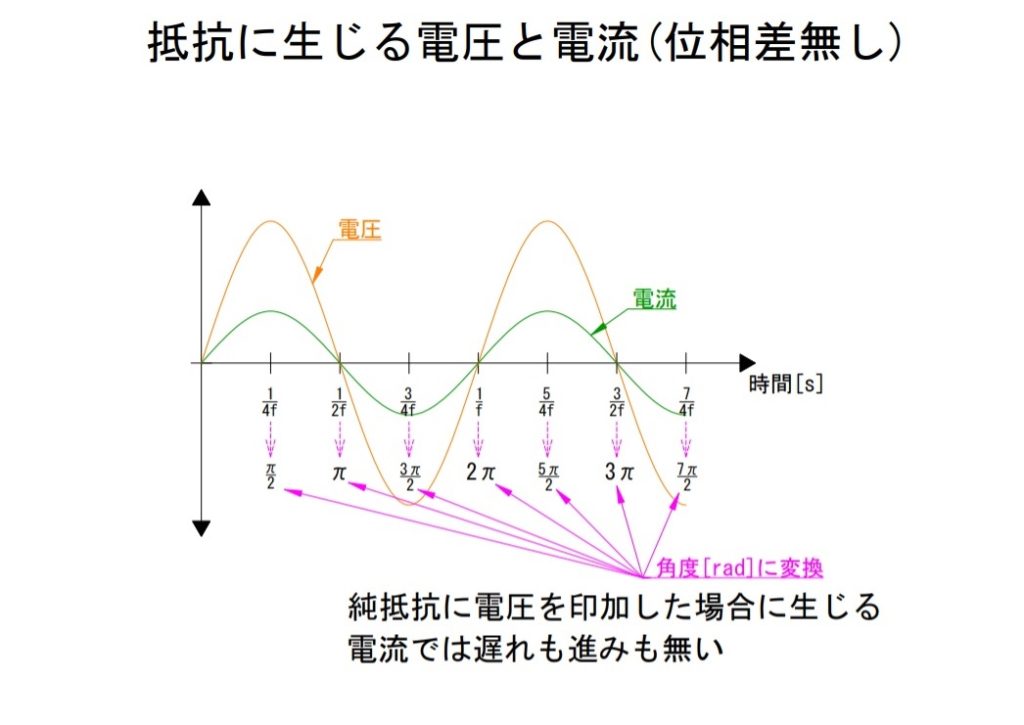
1)抵抗では遅れも進みもない
抵抗ではこれまでに説明したような無効成分は発生しません。すなわち電圧の変化と電流の変化にはタイミング的なズレはありません。
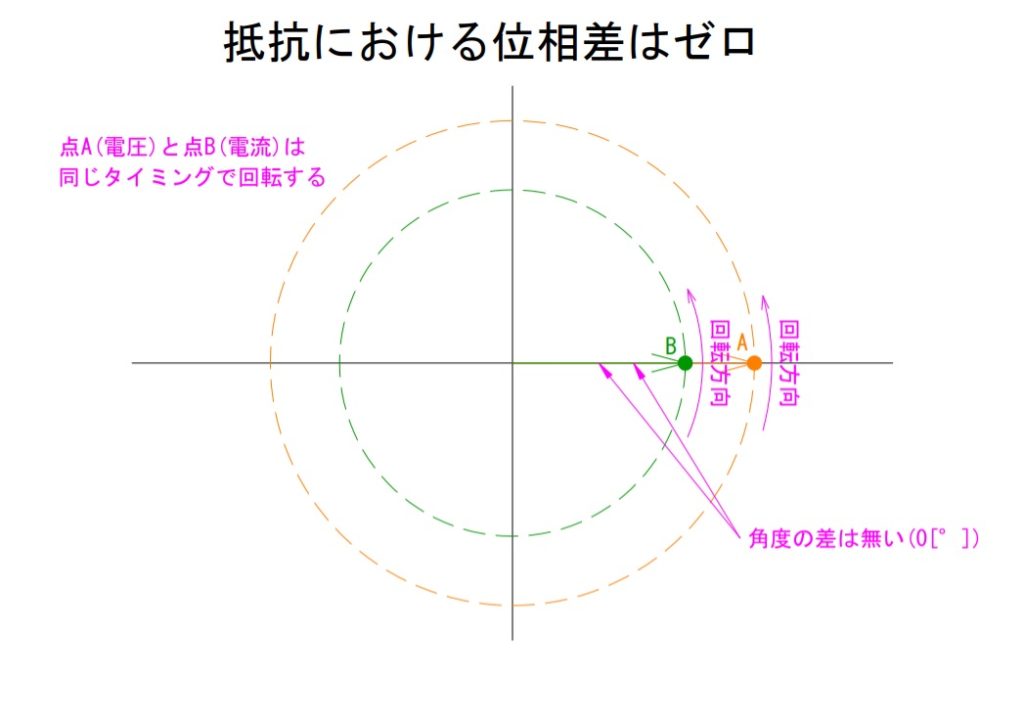
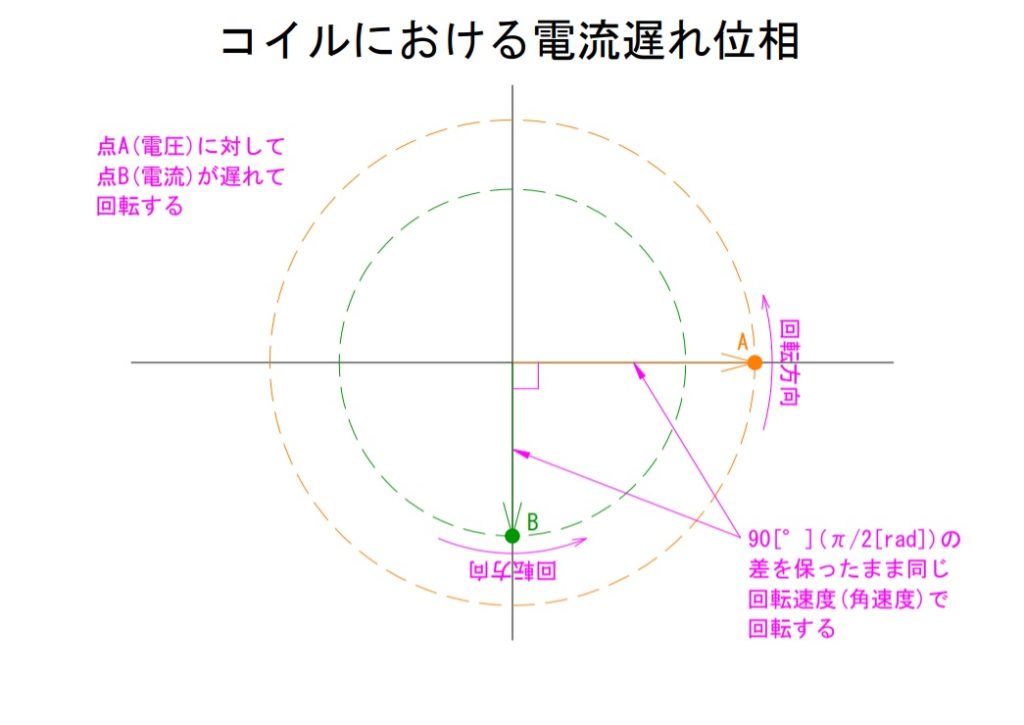
電圧と電流の遅れや進みについてもう少し説明するならば、ある半径ごとの同心円上を回転する点Aと点Bがあるとします。これらを各々電圧と電流に見立てます。そして点Aも点Bも1[回転]するのに例えば1[s]かかるとします(あくまでわかりやすさのため1[s]としています)。この一回転が上記のグラフの一周期に相当します。位相差が無いということはこの回転タイミングがぴったり一致しているということになります。
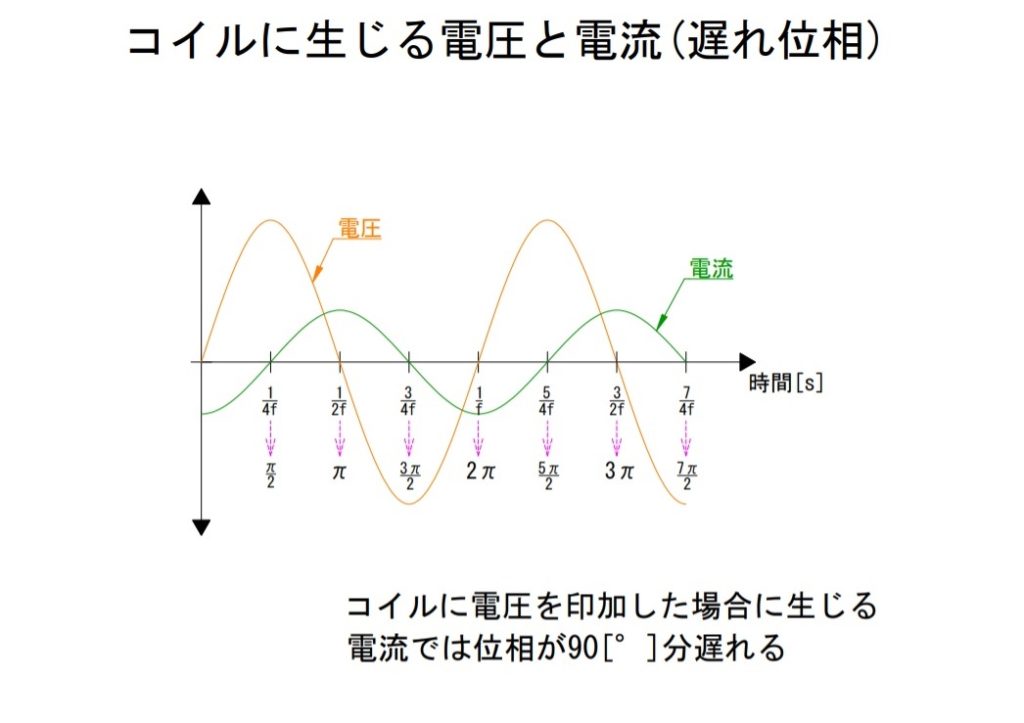
2)コイルは遅れ要素
位相の遅れを生じさせるのはコイルの性質となります。コイルでは電圧を印加した際に90°遅れて電流が生じます。コイルが挿入されている回路では電源とコイルが接続された瞬間にコイルでの電磁誘導という電流の発生を阻害する作用がはたらきます。その結果電流の発生は90°遅れることとなります。
では90°遅れるというのはどういうことでしょう。
抵抗の説明の時同様、点Aと点B、及び回転速度を1[s-1]とします。点Aに対して点Bが90°遅れるというのは、この場合では常に0.25[s]分遅れて点Bが点Aついてくるということを表しています。
上記の点Aを電圧、点Bを電流とすると、コイルでは電圧の変化に対する電流の変化は常に90°分遅れてやってくるということになります。これがそのまま無効電力としてあらわれます。
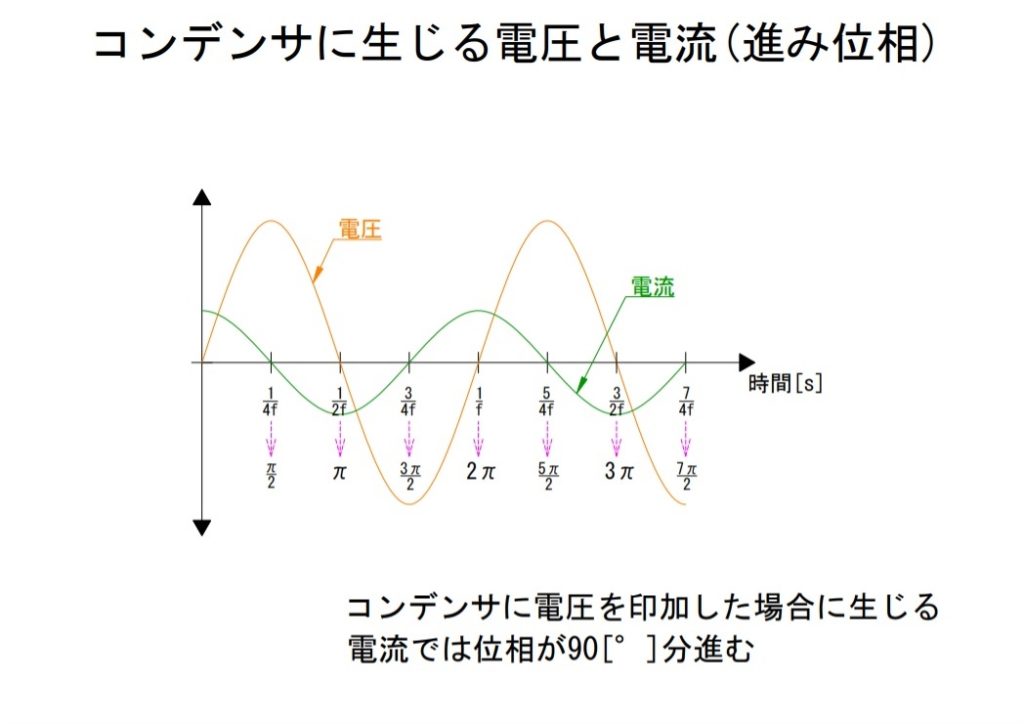
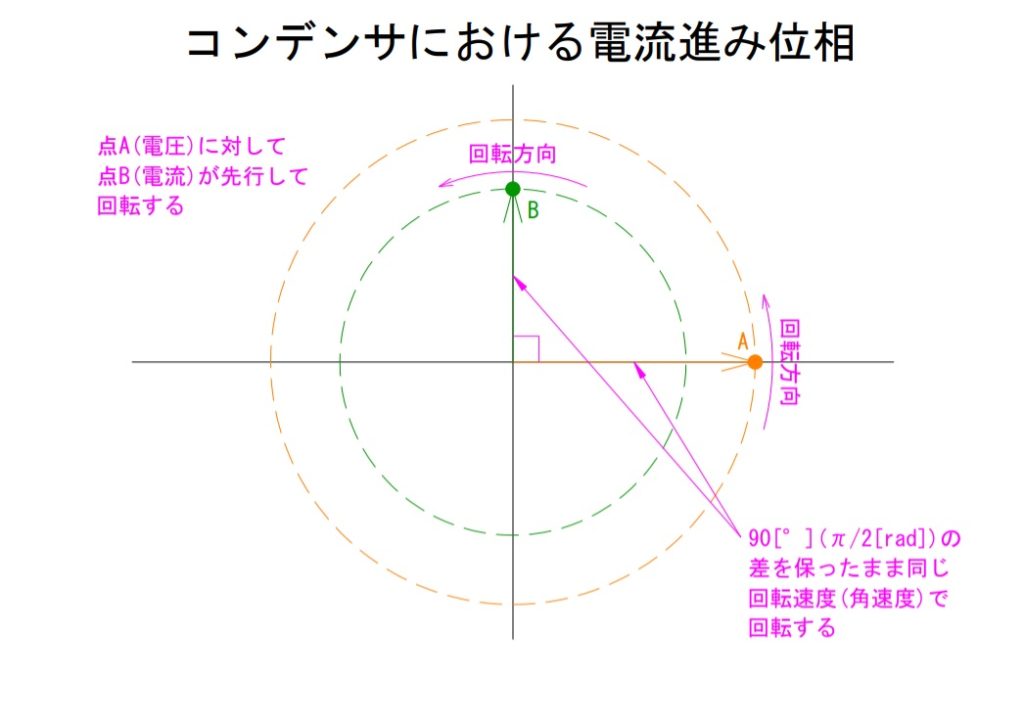
3)コンデンサは進み要素
位相の進みを生じさせるのはコンデンサの性質となります。コンデンサが挿入されている回路ではそのコンデンサと電源が接続された瞬間にコンデンサへの蓄電が開始されることで真っ先に電流が生じます。そしてコンデンサへの蓄電が進みその容量に迫るにつれ電圧があらわれるようになります。その結果電圧があらわれるより先に90°先行して電流が生じます。
90°進むというのはどういうことかということに関して、前述のコイルの項で説明した点Aと点Bの関係が逆になると考えてください。ですがあくまで基準は点Aつまり電圧です。
抵抗やコイルと同じように説明するならば、点Aに対して点Bが90°進むというのは、この場合では常に0.25[s]分だけ点Bが点Aに先行して回転するということを表しています。
コンデンサでは電圧の変化に対する電流の変化が常に90°分はやく生じることになります。そしてコイル同様、これがそのまま無効電力としてあらわれます。
3)コイルとコンデンサは打ち消し合う
ここまで、コイルとコンデンサの性質や影響について説明しました。すでに想像されている方もおられるかもしれませんが、このコイルとコンデンサの作用は互いに打ち消し合う性質をもっています。コイルによる誘導性の無効電力が大きい場合にコンデンサをもってしてその無効分を打ち消すことが可能であり、その逆もまた然りです。
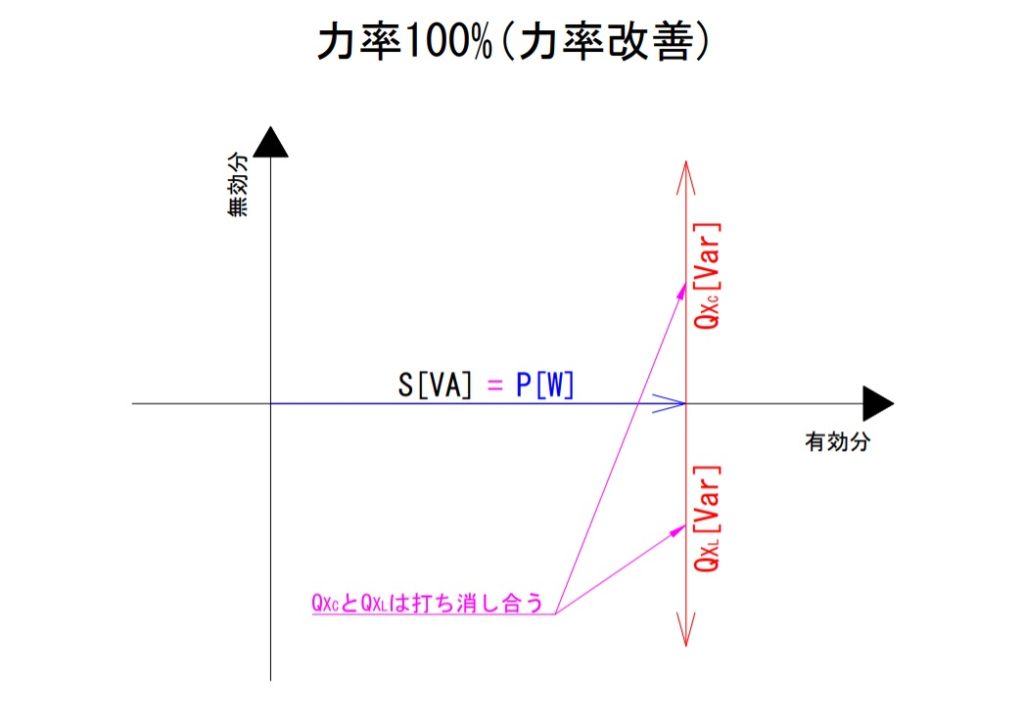
ということは、遅れや進みのどちらかに偏った回路でも打ち消す素子を回路内に挿入することで力率の改善を図ることができます。それを表現した図を以下に記載します。
力率が改善され、皮相電力と有効電力が近しくなっている様子や等しくなっている様子が表現されています。
5.電力を有効に!
電力には「有効電力」「無効電力」「皮相電力」という概念があることを説明してきました。またそのバランスにより「力率」という有効利用比率があり、それには「遅れ」や「進み」があることも説明しました。
電力を利用する際には前述のとおり、電力供給側からみても電力消費側からみても有効に消費するに越したことはありません。受変電設備や特に負荷の大きい電力消費機器ではこのことを考えて設計や保守管理を進めていく必要があります。
資源の乏しい国では特に必要な概念かと思います。
是非、この知識を有効に利用していただき、それをそのまま電力の有効利用へと役立ててください。
電験など難関資格取得は通信教育もアリ!
思い立ったが吉日!即行動で合格!!
![]()
三相電力計測に関して記事を作成しました。単相とは違い、3本の線で構成される回路の電力計測がどのように行われるのかまとめています。