1.電気と方程式,電気と関数
以前、電気を扱うに際して必要な数学知識として指数や対数に関する記事をまとめました。電気や制御に対する知識を少しでも深めていこうとするとき、どうしても数学の知識が必要となることが多くあります。
今回は「方程式」と「関数」について説明します。方程式や関数も、電気を扱ううえで必須の知識となります。簡単な部品選定から少し専門的な値の整定や設定などありとあらゆる場面で必要になります。
方程式の理解無しでは回路計算すらままならず、電気における基礎中の基礎である「オームの法則」の理解にも至ることはできません。
そして、関数も同様です。電気を扱う業務では場合によって「〇〇曲線」というグラフを相手にしなければならないこともあります。例えば各種「特性曲線」などから数値としての情報を取得する場合などです。このようなときに関数の概念や知識が無ければグラフが何を意味しているのか、数式をどう扱えば思ったとおりの動きをしてくれるのかがわからないという状態に陥ります。電気を扱うのであれば是非とも手に入れておきたい知識になります。
仮に数学に苦手意識があっても心配はありません。どちらかというと要領の良くない、あまり頭が良い方ではない筆者でも「ゆっくり着実に」を念頭において学習を進めた結果、ある程度は理解できてきました(もちろんまだまだ学び中ではあります)。
数学に苦手意識のある人は、一気に駆け抜けるのではなく着実に前に進むことを目標にしてみてはいかがでしょうか。
2.方程式
中学校で学ぶ数学で、多くの人が初めてふるいにかけられるような思いをするのがこの「方程式」という項目ではないでしょうか。数学に出てくるファーストステージのボスのような存在といったところでしょうか。「方程式」という字面や響きにも何だか難しそうなイメージが先行します。
そんな方程式ですが、解けたときの達成感やスッキリ感は労力の割に大きいのではないでしょうか。
1)方程式の形
方程式は以下のような形で表現されます。



上記はすべて方程式です。各々特徴はあるもののいずれも「方程式」という式の形に分類されます。上から「1次方程式」「連立方程式」「2次方程式」とよばれます。
いくつかの方程式の形を出しましたが、これらに共通するものは何でしょうか。
上のどの式でも「x」や「a」,「b」が、計算の結果どれか特定の値で定まるというところにあります。
式中にある「=」の記号を「等号」といいます。その左側の数式(数字)を「左辺」といい、右側の数式(数字)を「右辺」と言います。左辺と右辺が等号で結ばれる場合、その左辺と右辺は必ず等しくならなければなりません。これを「等式」と言います。これらのことから、方程式中の文字記号は自ずとある特定の値に決定されます。そして特定された値のことを方程式の「解」といいます。
2)1次方程式
これまで言葉で説明した方程式というものを実際に解いてみましょう。「1次方程式」というスタンダードで最もわかりやすい式を例にあげて説明します。
そもそも「1次方程式」とは式中に文字記号が一つのみ存在し、その文字記号の次数が「1」であるということです。次数が「1」というのは「1乗」であることを表し、「2乗」や「3乗」などの累乗(冪乗)ではないということです。表記でいうと「x2」や「a3」などの指数の文字記号は式中に含まれないということです。累乗や指数については指数・対数~電気計算で当然のように…~の記事で説明していますので参考にしてください。
おそらくですが、一般的には単に「1次方程式」というと「1元1次方程式」のことを指すと考えられます。「1元」は文字記号が一つであることを意味します。
まずは、この1次方程式で方程式とはどのような性質のものなのかを理解してください。
a.簡単な方程式 1

上の式も立派な方程式です。瞬時にその解が出てくるひとも多いのではではないでしょうか。
結論からいうと上の式の解は「x=3」となります。試しに「x」を「3」に置き換えてみてください。見事に等式が成立するのがわかります。この、「xを3に置き換える」という作業を「代入」といいます。「x」という箱の中に「3」という数値を入れて計算するというイメージです。
では、暗算で「3」とすぐに出てきたものの、いったいどのような手順をもってこの値は導かれたのでしょうか。わかりきってはいるかもしれませんが一度みてみます。
①移項
例の式は非常に簡単なのですぐにでも解が出ましたが、その中にひとつだけ大切な手順があります。暗算でもこの手順が無意識に実行されることが数多くあります。それが「移項」という作業です。
「項」を「移」すと書きますが、式中の「x」や「5」,「2」のようにその式を構成する値を「項」といいます。また、今回は見えない形ですが、「x」の前に表記される数字を「係数」といい乗算される値です。この例の係数は「1」ですので表記が省略されています。
式では「2」に何を足せば「5」になるのかということを問うています。このときに頭の中では「5-2」という計算が実行させることとなります。この「5-2」の形をつくりだす作業中に「移項」という大事な手順を踏みます。
移項は左辺と右辺にある項(数値や代数の加減算ではないかたまり)を各々移動することをいいます。




上記が解を導くための手順となります。上の手順の1行目と2行目が正に移項という作業になります。
②符号に注意
そして移項を実行する際に、気をつけなければならないことがあります。それが「符号」についてです。等式で移項をするときは移した項の符号を入れ替える必要があります。「正(+)」は「負(-)」へ、「負(-)」は「正(+)」へと入れ替えなければなりません。上記の式でも符号の入れ替えが行われています。
そして3行目では、左辺と右辺の各々に「-1」を乗じて(掛けて)符号の再整理をしています。最後の行では単純に減算(引き算)をした結果を表記し、これが直接「x」の解となっています。
b.簡単な方程式 2
もう一つだけ基本的な方程式を解いてみます。

上記のような式でも基本的な手順は同じです。ただし、先ほどと違うのは「x」に「6」という係数があることです。
ひとまずは、わかっている手順として移項をして符号の整理をします。移項時の符号の入れ替えに注意してください。


右辺の計算をします。

ここまできたらもう解が出ているも同然です。符号の整理をしたときと同様の考え方で解にたどり着きます。
等式では左辺と右辺に同じ処置をすることで等号を保ったまま、数値を都合のよい形に変えることができます。今回の例では左辺と右辺の両辺を「6」で除算(割り算)します。

解が出ました。実際に「x」に「3」を代入してみることで、等式が成り立つことがわかります。
また今回はわかりやすさのために途中に符号の整理作業を入れましたが、マイナス(負の数)のまま計算して最後に「-6」で除して(割って)も問題はありません。
c.分数なども同じ解き方
では、分数が方程式に混ざってきた場合はどのように処理すべきでしょうか。とはいっても、作業はほとんど同じです。下の例で説明をします。

まず、分数の式を自然数の式へと変形させたいので、両辺に「8」と「10」の公倍数である「40」を乗じます。
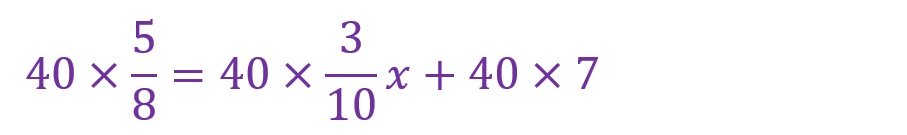

移項をします。

符号を整理しつつ、右辺を計算します。

両辺を「12」で除します。


解が算出されました。「x=-21.25」となります。特に、ルールや作業上のデメリットが無ければ解を分数で出しても小数で出しても問題はありません。
分母に対する処理があるものの、両辺に同じ値を乗じたり除したりすることで計算しやすくすることに変わりはありません。
大切なのは左辺と右辺の等式の関係を崩さずに計算しやすい状態へと変形することです。もちろん、分数のまま左辺と右辺を整理して通分を利用して計算しても問題ありません。
3)連立方程式
先程までは、方程式の最もシンプルな形として、1次方程式における解の出しかたを説明しました。
次いでここでは、「連立方程式」という計算について解説します。
連立方程式とは方程式二本以上から成る式のことをいいます。このとき出てくる文字記号も二つ以上になります。ただ、これだけではどのような方程式なのかイメージしにくいので、以降で例をあげて説明します。
a.2元1次の連立方程式を解く
いきなり「2元1次」なる単語が出てきました。これは二つの文字記号(2元)でかつ各々の文字記号はいずれも累乗されていない(1次)式となります。「連立方程式」という場合、まずはこの「2元1次方程式」が二本ある方程式が例にあげられます。以下のような式となり、これを「連立2元1次方程式」とよびます。

上記のような式が2元1次の連立方程式です。各々の式だけでは「x」も「y」も解は導けませんが、条件として二本の式が与えられることで解を出すことができるようになります。当然のことながら、解は「x」と「y」のふたつが導かれることになります。
つまり、上記二本の式を同時に満たす「x」と「y」を求めることが目的となります。
b.加減法で解く
またまた新しい単語が出てきました。「加減法」とのことですが、これはいったいどのような処理方法を言うのでしょうか。
平たく言うと式の状態のまま加算減算してしまおうという方法です。このときの加算減算には明確な目的があり、それは文字記号のある項のいずれかを相殺するということです。
そうすることで1元1次の方程式として扱えるようになった式の解を出すということです。
以下に処理の手順を記載します。
①相殺できる文字記号の項をつくる
加減法は、文字記号の項をひとつ相殺してしまうことが目的ですので、加算か減算で「0」にできる項をつくる必要があります。
例の連立方程式をみると「6x」と「3x」という項があります。「3x」は2倍すると「6x」になり、「6x-6x=0」をつくりだせます。
等式では両辺で同じ処理をすることができますので「24=3x+8y」の両辺に「2」を乗じます。

②減算(加算)する
二本の式の各々に「6x」ができましたのでこれを式ごと減算すると定数と「y」の項だけの式になります。どちらからどちらを減算しても良いです。
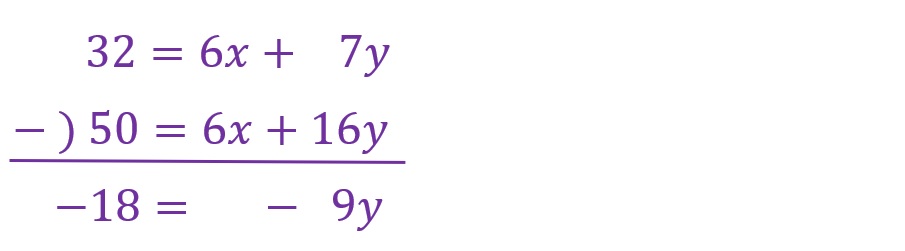


ひとまずは解の一つである「y」について「2」であることがわかりました。
もし、絶対値が同一で符号だけが逆の項がある場合は加算することで相殺します。
③判明した解を利用
続いて「x」についての処理をします。
すでに「y=2」が判明しているので、連立方程式のどちらかにこれを代入して「x」の解を導きます。
計算しやすそうな式をえらび「y」に「2」を代入したものが以下です。





よって

もうひとつの解である「x」について「3」であることがわかりました。
これで「x=3,y=2」という解答を得ることができました。
c.代入法で解く
連立方程式のもうひとつの解法として「代入法」というものがあります。
この方法では、先ずいずれかひとつの式において「x」または「y」について解きます。つまり「x=」か「y=」の形の式をつくります。次にこの式をを残ったもうひとつの式に代入することで解を出すというものです。
以下具体的にみていきましょう。
①式の変形

上の式のどちらかを、いずれかの文字記号について解きます。ここでは二本目の式を「y」について解きます。以下がその結果になります。



移項と両辺の処理によって上のような「y=…」の式が得られました。このような作業を式の変形といいます。
②式ごと代入
「y=…」を得られたところで、ここからが代入法の醍醐味です。まだ何も手を付けていない式の「y」に、変形した式をそのまま代入します。右辺の分数を含む式を括弧でくくる形で入れ込みます。

以下が代入した状態です。
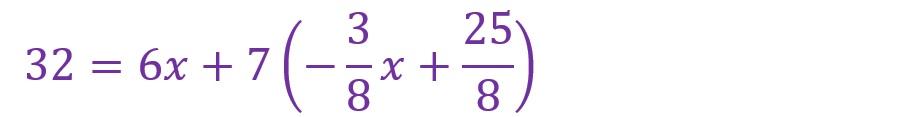
得られた式を展開して計算します。




「x=3」が解で得られました。
③判明した解を利用
「x=3」が判明したのでこの後は加減法のときと同様に、いずれかの式の「x」に「3」を代入して「y」の解を導きます。以下、手順です。




もう一つの解となる「y=2」が得られました。

加減法のときと同様に「x=3,y=2」という解答を得ることができました。
4)2次方程式
次に説明するのは「2次方程式」といわれる式です。文字記号は1種類のみですので「1元」なのですが、これは省略されています。次数が「2」ということですので最高次の文字記号は「2乗」されているということになります。
以下が2次方程式の例です。

パッと見ただけでは「x」がどのような値になるのか皆目見当もつきません。
解がどうなるのか、その解き方における考え方を説明します。
a.括弧でくくる
2次方程式はこれまでの方程式とは少しだけ計算過程が違います。移項やその他等式の性質利用などは変わりませんが、別の知識が必要になります。それが「括弧でくくりだす」という作業におけるものとなります。
具体的な手順を以降から説明します。
①移項して「0=…」をつくる

まずは元の式の定数を移項して「0=…」の式に変形します。「0=…」の形にするのには理由があり、これは以降の解法を読み進めることで自ずと明らかになります。
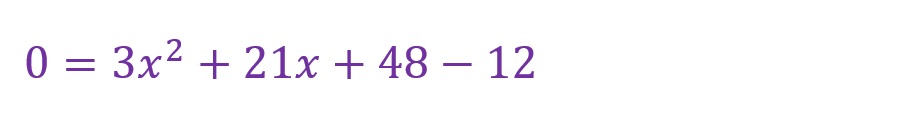

②括弧でくくるとは
いよいよ、「括弧でくくる」作業になります。
例の式ですぐにピンとくるのは、どの項も「3」の倍数であるということです。これを利用して括弧でくくります。

「括弧でくくる」という処理の正体は「式の展開」の逆操作です。このとき公約数として括弧の外に括りだされた「3」という値を共通因数といいます。
③さらに括弧でくくる
現状で「3」という値と括弧内の「x2+7x+12」という式の乗算の形ができました。
しかしながらこれでも「x」の解を計算しやすい状態であるとはいえません。式中に「x2」があることにより解の算出が難しくなっています。
「x2」をどうにかするためには再度括弧を利用することとなります。
注目すべきはもちろん「x2+7x+12」の式です。以下の展開公式と似ています。
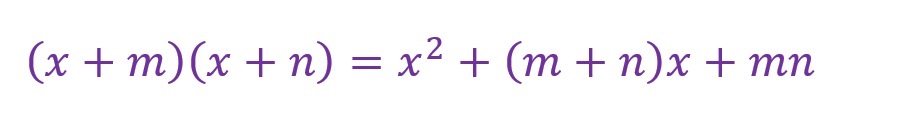
この公式を逆操作すると「x2」を回避することができます。
では「x2+7x+12」にどうアプローチすると「(x+m)(x+n)」の形にできるのでしょうか。
これまで注目してきた「x2+7x+12」の式と展開後の式をよく見比べてください。「7x」の「7」と「(m+n)x」の「m+n」,「12」と「mn」、これらは各々が対応しているようです。つまり「m+n=7」となり「mn=12」となる「m」と「n」を探せば良いのです。
それならばと連立方程式で解きたいところですが、そうしてしまうと計算過程に「m2」や「n2」が出てきてしまいます。せっかく2乗をどうにかして回避しようとしているのに新たな2乗をつくり出すのは全くナンセンスです。
そこで別の手段を講じる必要があります。ここで役に立つ方法として「たすき掛け」という便利な方法があります。この「たすき掛け」という解法について説明をします。
「x2+7x+12」のうち「x2」の前に隠れている「1」と「12」に着目し、各々を乗算の結果とする二つの値(ここでは整数)を割り出していく作業です。
まずは「1」についてです。乗算の結果が「1」、つまり「α✕β=1」となるとなる二つの値「α」「β」は最早ワンパターンでしかありません。「1✕1」です。ですので「α」も「β」も各々「1」となります。
次に「12」についてです。「α✕β」が「12」になる値については複数のパターンがあります。そのパターンは「1✕12」「12✕1」「2✕6」「6✕2」「3✕4」「4✕3」となります。
「1」と「12」の乗算パターンが出たところで各々をたすき状に乗算し、その結果を足し合わせたときに「7」となるパターンによって得られる値がここで得たい「(x+m)(x+n)」の「m」と「n」になります。
下の図をみてもらうと一目瞭然です。
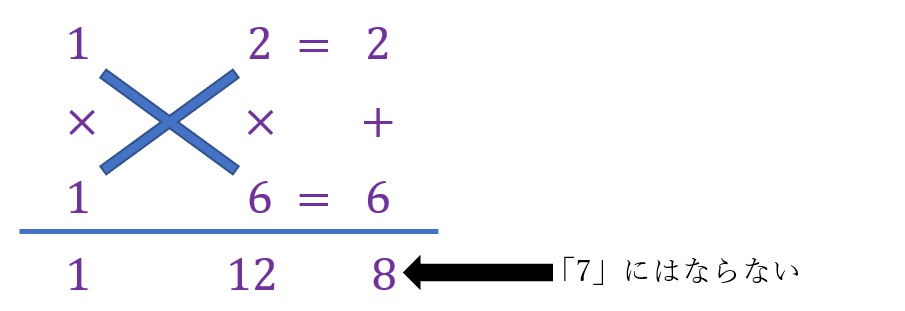
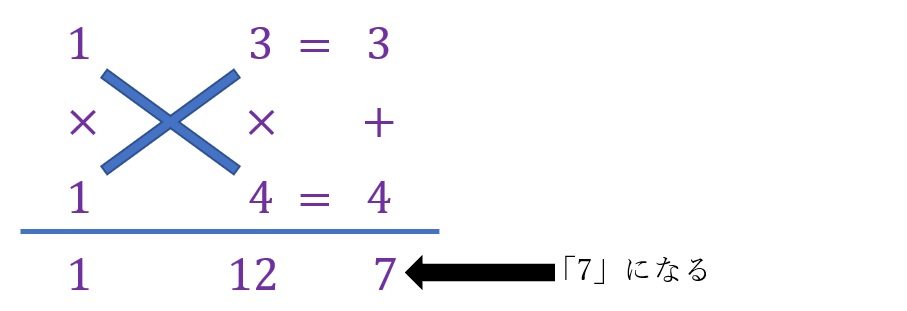
図の手順により「m」と「n」は各々「3」と「4」になります。この例題では「m」と「n」の値が入れ替わっても問題ありません。理由は符号がいずれも「+」であり値が逆でも計算結果に変化がないことにあります。
この結果をもとに括弧でくくると、以下の式が得られることになります。

実は、たすき掛けは「0=3x2+21x+36」の状態からでも可能です。「x2」の前の「3」と「36」に着目して、先ほどと同様に各々を乗算の結果とする二つの値(ここでは整数)を割り出していけば良いです。
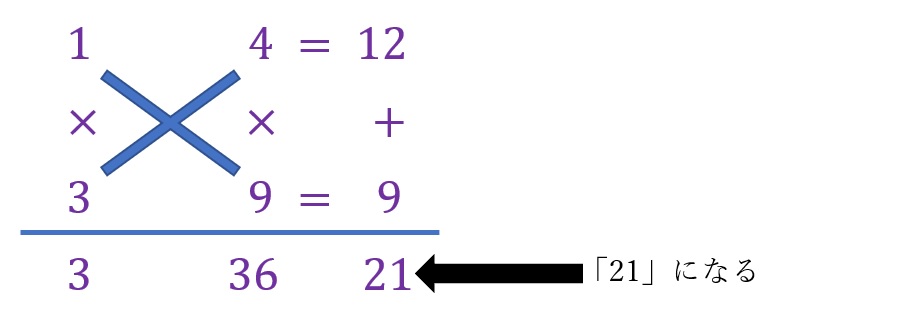
この場合は以下の式を得ることとなります。

ここまでの括弧でくくるという作業の全般を「因数分解」といいます。加減算として表された式を乗算の形にすることをいいます。因数分解は、これのみで充分に奥深い手法です。
④「0 = …」の式
ここまできたら、最早解は出ているようなものです。「0=3(x+3)(x+4)」の式で説明を続けます。
式は「0=…」なので右辺で「0✕…」をつくり出せば良いということになります。これが「0=…」の式をつくらなけらばならない理由となります。
右辺の「3」はもちろん変形しようがありませんのでそのままです。なにもアプローチする必要はありませんしできません。ということは「x+3」と「x+4」のうちどちらかを「0」にできれば良いです。
そうすると以下の二つの解が得られることになります。
・一本目の式


・二本目の式


よって、この例題の解は「x=-3,-4」となります。
「0=3x2+21x+36」から「0= (x+4)(3x+9)」という式を得た場合では因数分解が実質完了と考えて差し支えはありません。しかし、この場合の解の算出には注意が必要です。それは、括弧内に「3x+9」という式が混ざっているということです。「x+4」では「0=x+ 4」という式から単純に「x=-4」が算出できますが、「0=3x+9」は1次方程式を丁寧に解くか、再度因数分解(「3」で括る)かをして解く必要がありますので注意してください。
・一本目の式


・二本目の式



b.解の公式で解く
ここまで、2次方程式を「因数分解」を用いて解く方法について説明しました。しかし、因数分解を適用するには難解な式ももちろん存在します。そのようなときもそうでないときも抜群の力を発揮するのがこれから説明する「解の公式」というものです。2次方程式においてこんなに心強いものはありません。
①解の公式
では早速解の公式を以下に記載します。
2次方程式

解(解の公式)

2次方程式「0=ax2+bx+c」に対する、解を導く公式が上記となります。
ややこしい式にみえますが、公式ですので2次方程式の「a」「b」「c」を公式の「a」「b」「c」に当てはめるだけで解が得られます。「√」の前に「±」があるのは2次方程式には二つの解をが存在し得るということを意味しています(一つの場合もあります)。
②解の公式を使ってみる
ではこれまで解いてきた例題を、解の公式を用いて解いてみます。たすき掛けのときと同じ例題を記載します。

まずは「0=…」の形にします。

解の公式に当てはめます。
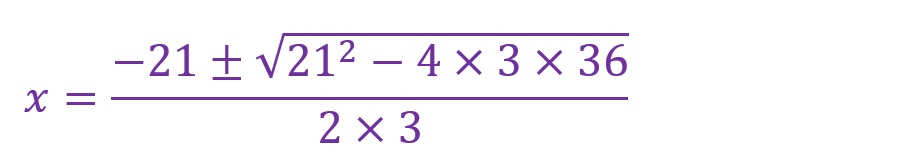
これを計算していきます。



・一つ目の解
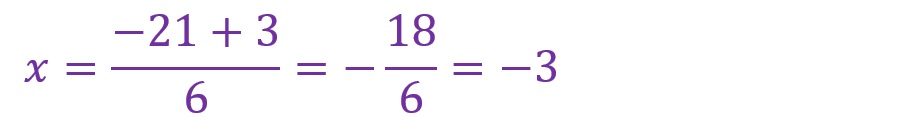
・二つ目の解
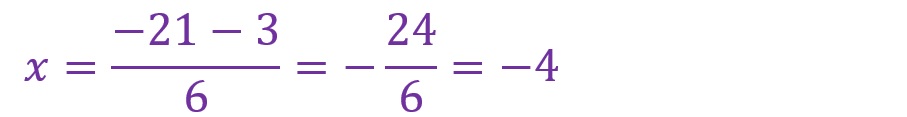

計算しやすい数値であったこともありますが、速やかに解が出ました。もちろん結果は因数分解で算出した場合と同様です。
5)高次の方程式
2次方程式までをみてきましたが、方程式にはもちろん3次や4次それ以降も存在します。解法としては2次方程式までの応用で対応可能ですが、各々の次数における展開公式や因数分解を利用することとなりますのでその複雑さは格段に増すこととなります。
3次や4次での解の公式(筆者は覚えていません)もあるようですがかなりの長文公式となるようです。
必要に応じて高次の方程式も解けるようになるとなお良いかと考えます。そのためにはより高次の展開公式や因数分解を使いこなすことが必要となります。
3.関数
方程式からさらに数学らしさを増すのが、見出しにある「関数」という項目です。「関数」ももちろん忌み嫌われることが多く、この文字を見ただけで拒絶反応が出る人もいるでしょう。
ですが、この関数というものは事象を説明するのに非常に便利な考え方であり、論理的思考を必要とする場面では特に重要な役割を果たすことがあります。
以降から、あくまで概念程度としての説明になりますが、関数の種類と共にその扱いについて簡単な例をあげて説明します。
1)関数とは
では、まず「関数」というものが何者であり、どのような性質をもつのかについて説明します。定義文はありますが解釈が難しいので、あえて筆者の言葉で説明します。
「関数」とは【「独立変数」と「従属変数」、場合により「定数」から成り立つ、ある事象の変化の根拠を説明するための数式。】のことと認識して差支えはないでしょう。
「独立変数」は能動的に値を決定することができる変数と考えてください。「従属変数」は独立変数と数式で受動的に値が決定される変数と考えてください。「能動」「受動」とはありますが、逆算的に使用することも可能です。
関数の中には変数が三つ以上あるものも存在します。このような関数のことを「多変数関数」といいますが、ここでは一般的な「2変数関数」で話をします。
2)関数の種類とグラフ
一言で「関数」といっても、その形態は数多く存在します。そのため関数は種類によって「〇〇関数」というよばれ方をします。「三角関数」などは多くの人が一度は聞いたことのある単語ではないでしょうか。
関数の表記として「f(□)」という表現方法を使用します。「f」は「関数」の意味をもつ「function」の頭文字です。同時に二種類の関数を表現する際の二本目の式で「g」を使用することもあります。
そして「f(□)」は「変数□をもつ関数」であることを意味します。「□」には一般的に「x」などがよく使用されます。
記号の使用に関しては、上で述べた「f」や「x」などが一般的ですが、もちろん任意であり別の記号を割り当てても問題があるというわけではありません。
式の変数が「x」である場合、その関数は「f(x)」と表現することができます。このときの変数「x」が独立変数ということとなります。

また、関数「f(x)」の独立変数「x」により値が決定されるもう一つの変数にも文字記号を割り当てることができます。一般的には「y」を用います。このときの左辺と右辺の関係を以下のように表現することができます。
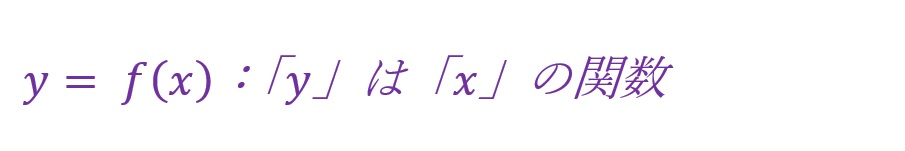

上記の例では、「y」の値は「x」の値とその数式によって決定されます。このときの「y」を従属変数といいます。
関数の内容が「ax+b」であり、変数が「x」となる場合「f(x)=ax+b」と表すことができます。そしてこのとき「y=f(x)」であるならば「y=ax+b」と表すことができます。ということは少し強引に表現すると以下のように表すことも可能です。

この例でも前述同様に「x」が独立変数であり「y」が従属変数となり、さらに「y」は「x」の関数であるといえます。
関数は各変数の関係性について、計算式の形で表現されます。そしてその計算式はグラフと共に表記されたり、グラフ化が必要となったりします。関数をグラフ化することで独立変数の変化により従属変数で表される結果がどのように変化するのかを視覚的に捉えることが可能になります。少し電気的に表現すると、グラフ化によって「入力に応じた出力の様子を視覚的に捉えることができる」ということになります。
以降から、独立変数を「x」として、従属変数を「y」として話を進めます。
a.1次関数
関数の最もシンプルな基本形である「1次関数」について説明します。
①1次関数の式
1次関数の式は以下のようになります。

変数(ここでは「x」)が累乗(冪乗)されていない関数です。「a」は「係数」といい、「x」に乗じる値です。「b」は「定数」といい、ある一定の値となります。「a=1」で「b=0」の場合「f(x)=x」となります。
例えば「a=2」で「b=5」であるときの関数は以下になります。

②1次関数のグラフ化
「y=f(x)」とすると以下のグラフが得られます。


この関数の中にある「2」は直線の傾きの度合いを表し、「5」は直線の原点(x = 0,y = 0の点)に対するシフト(ずれ)量を表しています。比較として以下のような関数をグラフ化してみます。もちろん「y=f(x)」が前提です。


係数が減ると共にグラフの傾きが緩やかになるのが確認できます。また、定数の変化と共に直線とy軸(x軸)との交点が変化しているのがわかります。
係数で表されるグラフの傾き、すなわち「a」は独立変数の変化に対する従属変数の変化量の割合になります。先ほどまではこの「a」が正の数である関数を例としていたのでいずれも右肩上がりの直線になりましたが、「a」が負の数ならば傾きは逆になり右肩下がりのグラフになります。つまり変化量がマイナスであるということです。
定数「b」は直線と軸との交点を表すと述べましたが、これを確かめる方法としては独立変数に「0」を代入すると良いです。つまりここでいう「x」を「0」にするということです。


従属変数「y」が「5」となりました。「x=0」のとき「y=5」で直線はy軸と交わるということになります。
なお、「x=0」のとき「y=5」になるポイントを「(x,y)=(0,5)」と書き表すことができます。このようなグラフ上のある一点を表現した値の組み合わせを「座標」といいます。
1次関数ではそのグラフが直線の形をとります。変数の前に付加される係数がその直線の傾きを表し、定数は軸との交点を表します。
b.2次関数
1次関数より少し発展した「2次関数」について説明します。
①2次関数の式
2次関数の式は以下のようになります。
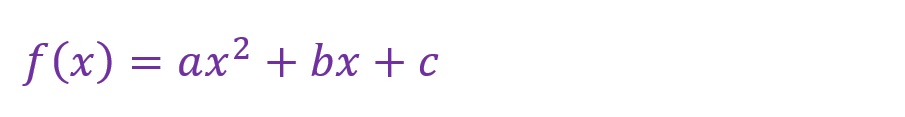
最高次の変数(ここでは「x」)が2乗されている関数です。「a」「b」は1次関数同様「係数」といい、「x2」や「x」に乗算する値です。「c」も1次関数同様に「定数」といい、ある一定の値となります。「a=1」で「b=0」また「c=0」の場合「f(x)=x2」となります。
例えば「a=2」で「b=4」,「c=6」であるときの関数は以下になります。

②2次関数のグラフ化の前に
「y=f(x)」とし、グラフを作成したいところではありますが、2次関数の場合はグラフ化の際にひと手間必要になります。このひと手間は「f(x)=ax2+bx+c」の式を「f(x)=a(x-p)2+q」の形にするというものです。
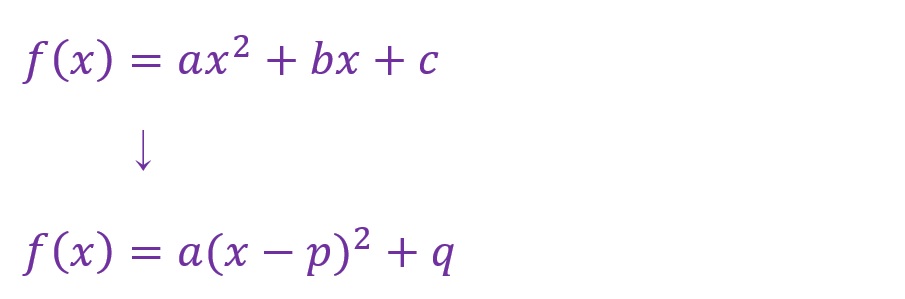
この形にすることではじめてグラフが描けるということになります。そしてこの処理のことを「平方完成」といいます。
以下に平方完成の実施手順を、先ほどの例を用いて記載します。

先ず「x」の付加されている項を「x2」の係数つまり「2」で括ります。

括弧内の「x」の係数を「2」の倍数の乗算へ変形します。
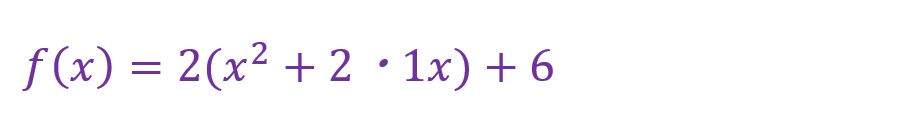
「x」に付加されている「2」以外の係数(ここでは「1」)を2乗し加算した後減算する形をつくります。
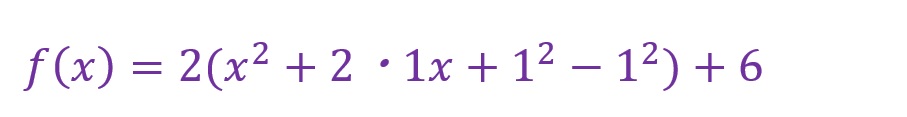
括弧内の「x2+2・1x+12」を因数分解公式に則って因数分解します。
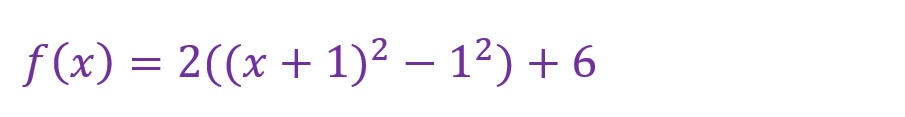
「(x+1)2」を保持したまま外側の括弧のみを展開し計算します。
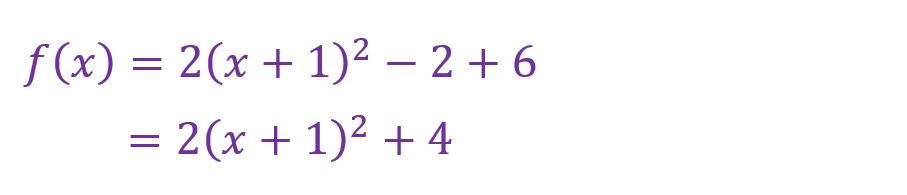
例題では「p=-1」「q=4」となりました。
一般式でも計算してみます。
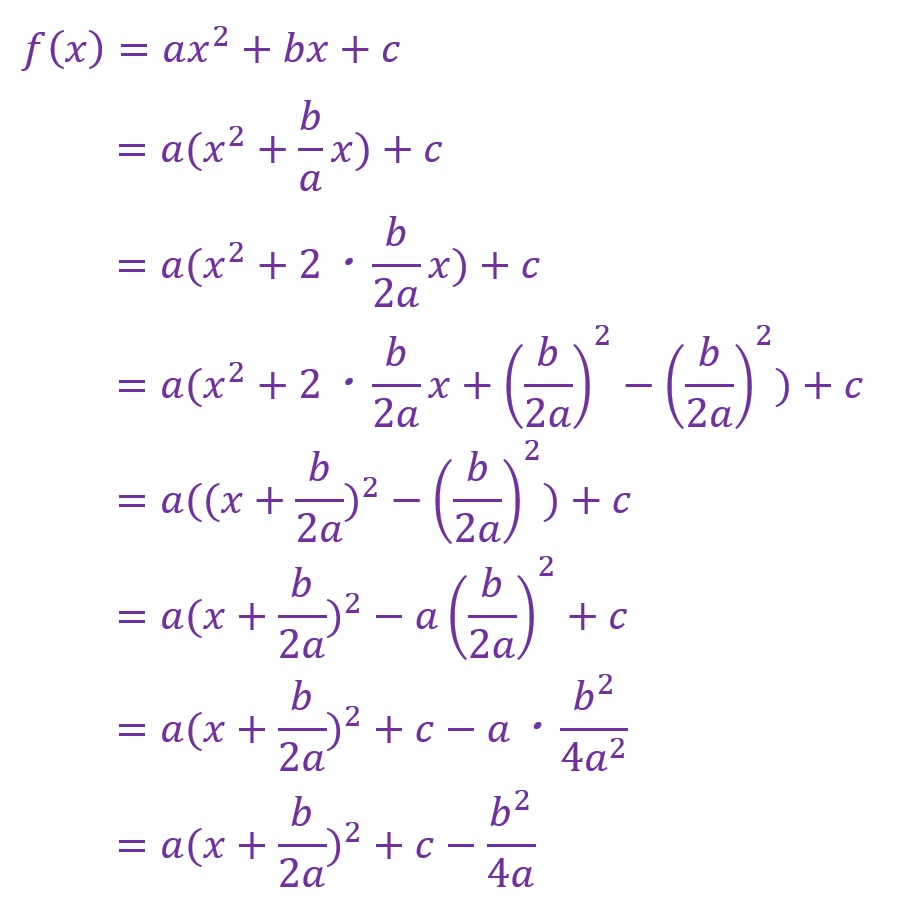
一般式では以下のような値が得られます。
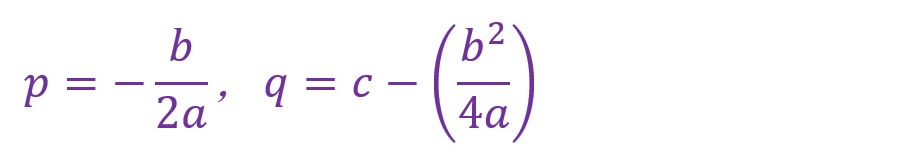
やっと「f(x)=a(x-p)2+q」と同じ形の式が得られました。「p」における符号の違いがありますのでここには注意が必要です。
③2次関数のグラフ化
では、なぜ「f(x)=a(x-p)2+q」の形の式がほしかったのでしょうか。その理由は「p」「q」が2次関数のグラフの頂点座標を示す値となるからです。
2次関数のグラフは上に凸か下に凸の「放物線」になります。放物線は字の如く、ものを投げたときの軌跡に似ていることから名付けられています。そしてこの放物線の頂点が座標上の(p,q)になるということです。
今回の例では「(x,y)=(-1,4)」という頂点座標が得られたということです。
ここまでに得られた頂点座標と他のポイントをつなぐことで2次関数のグラフを描くことができます。「y=f(x)」としたグラフを以下に記載します。
頂点に関してはここまでに述べたとおりですが、この関数の中にある括弧にかけられた「2」という値はやはり係数となり、描かれる放物線の開き方の度合い、言い換えれば開度を表します。係数が大きければ大きいほど放物線の開度は狭くなり、鋭く尖ったようになります。またこの係数が負の数である場合は放物線が上に凸の曲線になります。
係数と頂点座標の違いによってグラフがどうなるかをみてみます。以下の式のグラフを追加で載せます。
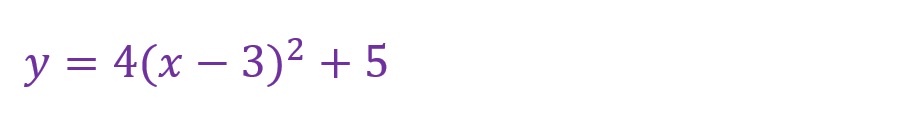

係数の増減と共にグラフの開度が変わっていることや係数の符号により凸の方向(上下)が入れ替わることが確認できます。また頂点座標によって曲線の頂点位置が変わることも確認できます。
2次関数ではそのグラフが放物線の形をとります。グラフ化のためには平方完成という手法を用いて「f(x)=a(x-p)2+q」の式をつくる必要があります。
括弧の前につく係数は符号と共に放物線の開度と凸の向き(上下)を決定し、式でいう「p」と「q」が放物線の頂点位置を決定する座標となります。
c.(1次)分数関数
ここでは分数の形で表される「分数関数」というものについて説明します。分数関数にも次数がありますが、ここでは1次の分数関数についての説明とします。
①(1次)分数関数の式
(1次)分数関数の式は以下のようになります。

分数関数では分母に変数(ここでは「x」)が存在することとなります。分子のみに変数があるだけならば見た目が分数でもそれは単なる1次関数ですので混同しないように注意してください。
②1次分数関数のグラフの特徴
1次分数関数のグラフは「双曲線」という形をとります。「双」という文字が入っていますが、これは曲線が二つ存在することを述べています。1次分数関数では点対称位置に二つの曲線が描かれるということです。またこのグラフには「漸近線」という値(ライン)が存在します。1次分数関数での変数は、この漸近線で示される値に限りなく近づきますが決して到達することはありません。
漸近線における簡単な例として、以下の式を用いて考えます。

上の式で変数「x」に「1」から順番に自然数を代入してみます。結果「y」は「1」「1/2」「1/3」「1/4」…と減少していきます。さらに「x」を増やして「1000」「10000」「100000」…と代入すると「y」は「1/1000」「1/10000」「1/100000」…と限りなく「0」に近づきます。しかし決して「0」になることはありません。
式を変形して「x=1/y」としても現象に変わりはありません。「y」がどんなに増えても「x」が「0」になることは無く、しかし「0」へと限りなく近づいていきます。
このときに「x」と「y」の各々で、限りなく近づきはするものの決して到達しない値で形成されたラインを「漸近線」といいます。直交する漸近線を有することも1次分数関数の大きな特徴です。
③(1次)分数関数のグラフ化の前に
1次分数関数のグラフの特徴について最もシンプルな「f(x)=1/x」を例に説明しました。その特徴は、原点(x,y)=(0,0)で直交するライン、つまり「x」軸と「y」軸を漸近線とする双曲線ができるということでした。
では、一般的な1次分数関数のグラフは「f(x)=1/x」に比べどのような違いがあるのでしょうか。これについて説明します。
なお、この項目の最初に出てきたような分数関数は、そのままではグラフ化することができません。グラフ化のためには以下のような式に変形する必要があります。
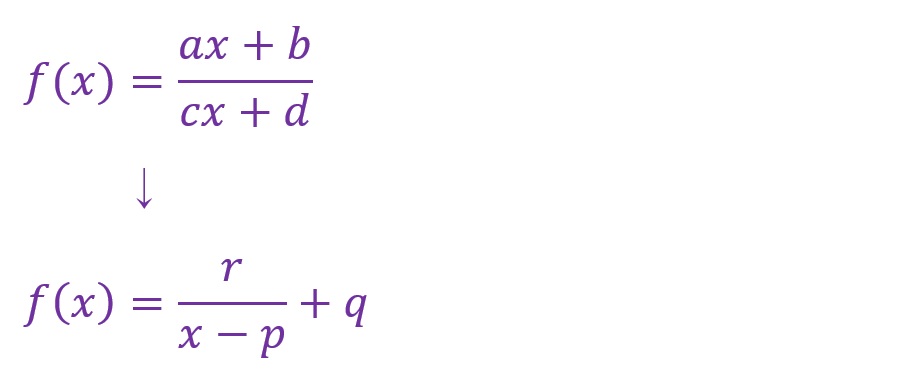
先ずは、その変形について手順を追っていきます。早速ですが以下の式を例に変形過程を記載します。「a=1」「b=6」「c=2」「d=4」とします。

先ず、分母の式を強引に分子の式へ入れ込む作業をします。分子の「x」に掛かる係数「1」を分母の「x」に掛かる係数「2」で除した値をつくります。つまり分子に「1/2」をつくります。そこに分母の「2x+4」を乗じます。結果、分子が「(1/2)(2x+4)+6」となります。しかしこのままだと、これを展開したときに「(1/2)✕4=2」という値が余分に出てきてしまうので、これを差し引く形にします。そうすることで分子は「(1/2)(2x+4)-2+6」の形になります。
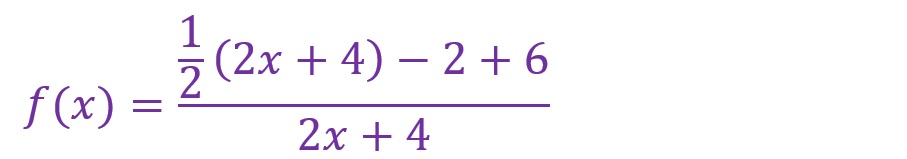
分数の加減算の形にします。
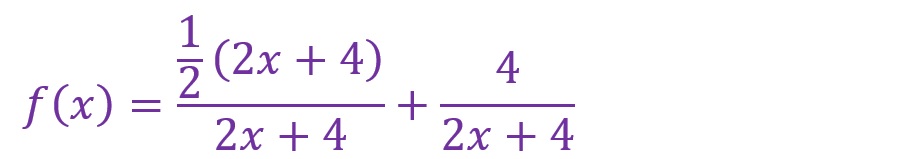
「(1/2)(2x+4)/(2x+4)」について約分します。

「(4/(2x+4))」について「2」で約分します。
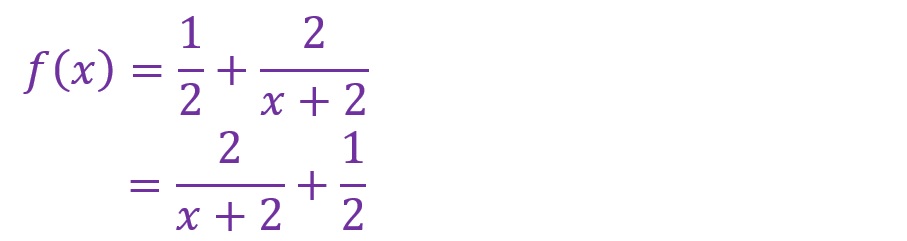
この例題では「r=2」「p=-2」「q=1/2」となりました。
一般式でも計算してみます。
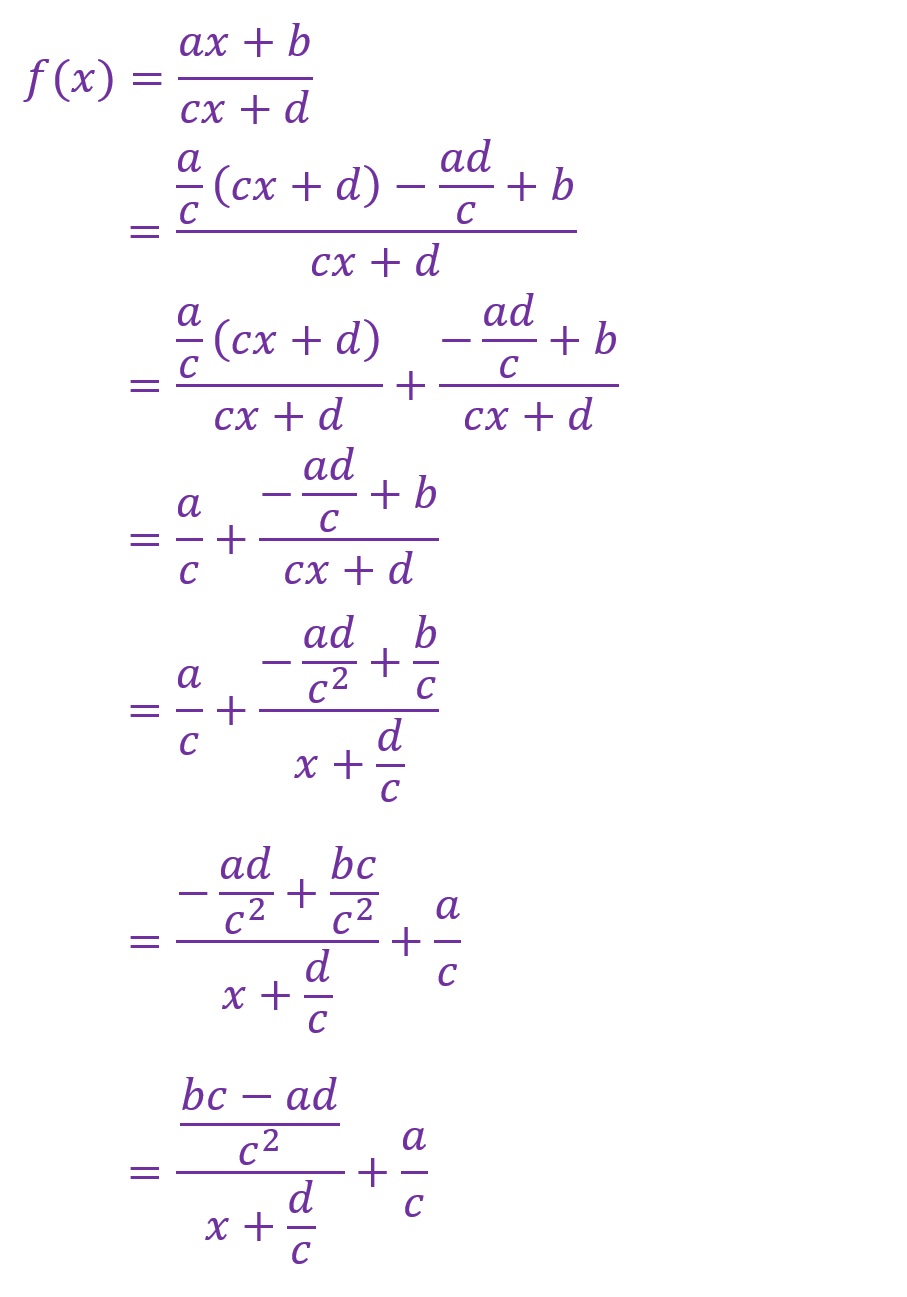
一見、欲しい形には全くなっていないような気がします。しかし、「(bc-ad)/c2」と「d/c」そして「a/c」は定数ですのでこれらを各々「r」「p」「q」と置き換えてみるとグラフ化に必要な形になっていることがわかります。

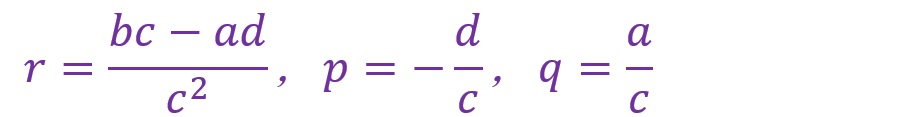
式の変形が完了したことでグラフ化のための準備ができました。
③1次分数関数のグラフ化
式の変形が完了したのであれば、この関数をグラフ化することができます。
前の項で変形した式をグラフ化してみます。「y=f(x)」とします。
漸近線の位置が「x」方向に「-2」,「y」方向に「1/2」移動した形になっていることがわかります。
この他に以下の例も混じえて係数の変化などもみてみます。


1次分数関数ではそのグラフが双曲線の形をとるとのことでした。双曲線は点対称に二つの曲線が存在するということであり、さらに各曲線には漸近線という限りなく近づくが決して到達しないラインがあります。グラフ化の式における「p」「q」は各々横軸と縦軸における漸近線の値を示しています。
d.指数関数
「指数」とは「底」で示される値が繰り返し乗じられている(掛けられている)ときの繰り返し数をいいます。詳しくは 指数・対数~電気計算で当然のように…~の記事にまとめていますのでこちらを参考にしてください。
ここで説明する「指数関数」は先で説明の繰り返し乗じる回数、すなわち「指数」が独立変数である関数となります。
①指数関数の式と特徴
基本的な式は以下のようになります。

係数や定数が付加される一般的な式は以下になります。
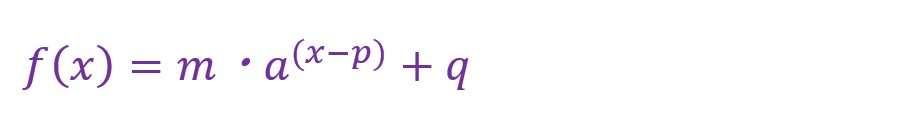
ここではわかりやすさのために「p=0」「q=0」「m=1」とします。つまり「f(x)=ax」が例となります。ただし、「a」は実数の範囲とします。これについては「a」を負の数とした場合に「虚数」という平方根の中が負の数となる数値を扱うこととなり、話が複雑になることからここでは割愛します。
指数関数で表される計算の結果は非常に大きな変化量を伴います。仮に「底」が「2」である指数関数でみてみます。式は「f(x)=2x」となります。
変数「x」が「1」のときは「f(1)=2」、変数「x」が「2」のときは「f(2)=4」となりさほど大きな変化は無いように感じます。しかし、さらに変数「x」に代入する値を大きくしていくと、得られる値の変化が顕著になります。変数「x」に「5」を代入すると「f(5)=32」となり、「6」を代入すると「f(6)=64」、「7」を代入すると「f(6)=128」という具合に得られる値は倍々で増加します。「底」が「3」や「4」それ以上になるとその増加量は変数に代入される値が「1」増えるだけで3倍,4倍またそれ以上になります。
余談ですが、このような特徴から日常生活でも、時間の変化等に伴い著しい変化量で増減する事象に対して「指数関数的な変化」と表現することがあります。例えば「彼の成長は指数関数的だ。」などといった具合です。
また「f(x)=ax」の指数関数は次のような特徴も合わせ持ちます。
a.いかなる「底」であっても「x=0」では得られる値(f(0))は「1」となることです。このことは「指数法則」にもあり、指数・対数~電気計算で当然のように…~の記事にもまとめています。
b.「底」が「1」であれば、変数「x」が何であれ「f(x)」はいかなる場合も「1」となります。当然といえば当然ですね。「1✕1」を何度繰り返しても得られる結果は「1」です。
c.「底」が「0」でない場合、つまり「a≠0」であれば真数「f(x)」が「0」になることはありません。変数に、負方向(マイナス)に大きな値を代入していったとしても、限りなく「0」に近づきはしますが決して「0」にはなりません。つまり「y=0」を漸近線とするということになります(「y=f(x)」が前提です)。
d.指数関数の大きな特徴として、「a」がどの範囲にあるかが変化の方向を決定します。具体的には「a」が「1」を超える場合はグラフが右肩上がりとなり、「1」未満の場合はグラフが右肩下がりとなります。これについてはグラフ化のところ(後述)を参照してください。
指数関数を理解するにあたって、非常に大切なことがあります。それは指数法則の理解です。これに触れずして指数関数を理解するのはかなり厳しいです。
②指数関数のグラフ化
なお、「f(x)=ax」の指数関数をグラフにすると以下のようになります。「a>1」の範囲では「a=2」を、「0<a<1」の範囲では「a=0.5」を例にグラフ化します。もちろん「y=f(x)」が前提です。
先に説明のとおり、「a>1」では右肩上がりのグラフが描かれます。対して「0<a<1」の範囲ではグラフは右肩下がりとなっています。また、上記二つのグラフでは一見「y=0」になっているように見えますが数値が非常に小さいためにそう見えるだけであり、実際は「y=0」になってはいないということに注意してください。
ここで説明の式はごく基本的な「f(x)=ax」という形のものでしたが、前述で少しだけ触れたとおり、「f(x)=m・a(x-p)+q」のように係数や定数が付加される場合もあります。
このような場合は変数「x」が「0」だったとしても「f(0)」は「1」にならなかったり、漸近線がずれたりします。ですが係数が付加されても定数の加減があったとしても指数の計算における規則である指数法則から外れなければ自ずととるべき座標がわかります。少し形が変わっていても焦らずに対処するのみです。
e.対数関数
指数関数が出てきたのであれば、「対数関数」を出さないわけにはいかないでしょう。対数は指数の逆処理のようなものです。対数に関する説明も指数・対数~電気計算で当然のように…~にまとめていますので参考にしてください。
①対数関数の式と特徴
対数が指数の逆処理であることは広く知られています。指数関数と対数関数のような表裏の関係を「逆関数」の関係といいます。対数関数は指数関数の、指数関数は対数関数の逆関数であると表現します。
対数関数はその算出結果(f(x))が指数そのものとなります。このことは、独立変数「x」が大きくなっていっても、「f(x)」の変化量が小さいことを意味します。指数関数を逆からみるわけですので自然なことです。
対数関数の最もシンプルな式は以下のようになります。

係数や定数が付加される一般的な式は以下になります。
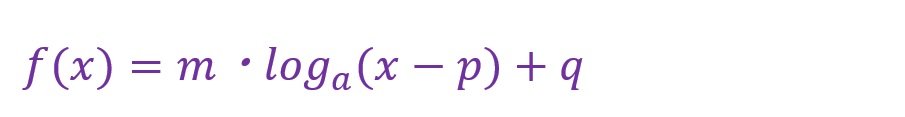
以降は指数関数のときと同様に「f(x)=logax」で対数関数を説明します。ここでも、わかりやすさのために「p=0」「q=0」「m=1」とするということです。また、これまで同様「y=f(x)」が前提です。
ただし、「a」は「0」より大きくまた「1」ではない範囲とし、変数「x」も負の数ではない範囲とします。ここで「底」に負の数を用いない理由は指数関数のときと同様です。
この式において「x」は「真数」といい、「底」である「a」が繰り返し乗じられた(冪乗)結果となる値です。そして「f(x)」で算出される値こそが「対数」であり、「指数」と全く同じ意味をもち、視点(基準や起点)のみが違うという値です。
②対数関数のグラフ化
「a=2」を例に説明を進めます。式は以下のようになります。この式を例にグラフ化の説明をします。これまでのとおり、前提は「y=f(x)」です。

指数関数「f(x)=ax」の場合、「a」がいかなる値であっても変数「x」が「0」ならば「f(0)=1」となりました。対数関数は指数関数の逆関数ということですので似たようなポイント(座標)があるはずです。といっても、この答えは単純で「x=1」のとき「y=0」となる座標です。変数であると同時に真数である「x」が「1」であるならば「y=f(1)=log21=0」となります。
また、対数関数が指数関数の逆関数であることから推測できますが、この対数関数のグラフにも漸近線が存在します。漸近線がどこになるのかを考えます。
先ほど「y=log2x」のグラフでは「x」が「1」のとき「y」が「0」となりました。では、試しに「x」が「0」のとき「y」はいくつになるのでしょうか。式として書き出すと以下のようになります。

「2」が「0」になるためには何乗するとよいのでしょうか。結論からいうと上記のような「log20」という値は定義されません。これは「loga0」でも同じです。「2」であろうが「a」であろうがこれらを何乗しても、正確には負方向(マイナス)に何乗しても限りなく「0」に近づくものの、決して「0」にはなりません。つまりこれ(「x=0」)が漸近線ということになります。
x軸との交点および漸近線が判明しましたので、あとは複数の座標がわかれば、以下のようなグラフが描けることになります。
また、指数関数のときと同様に、「a>1」では右肩上がりのグラフが描かれます。対して「0<a<1」の範囲ではグラフは右肩下がりとなっています。また、上記二つのグラフでは一見「x=0」になっているように見えますが数値が非常に小さいためにそう見えるだけであり、実際は「x=0」になってはいないということに注意してください。
「y=log2x」をグラフ化できたところで、「y=2x」と見比べてみます。共に「a=2」で係数や定数の付加が無いことが共通点です。互いの式におけるグラフを同一の平面に描画すると以下のようになります。
これらのグラフを見比べてみたとき、どうにかすると二本の曲線はピッタリと重なり合うような気がします。
実はこの二本の曲線は「y=x」を軸とした線対称図形となります。「底」や係数,定数などの条件が同じである場合、紙面に描き出された指数関数と対数関数のグラフは、「y=x」で折り曲げるとピッタリ一致するということです。これが、対数関数は指数関数の逆関数であるといわれる視覚的な理由です。
指数・対数~電気計算で当然のように…~の記事でも述べていますが、対数には「常用対数」と「自然対数」という、基準となる「底」をもつ対数があります。常用対数では「底」は「10」であり、自然対数では「e」となります。対数関数を扱うときに、「底」が今ひとつピンとこない値である場合は特に数値的にわかりやすい常用対数へ変換するとイメージしやすい値になります。
そのためには、「底の変換公式」が必要になりますが、これも指数・対数~電気計算で当然のように…~の記事で説明しています。

f.三角関数
「関数」といわれたとき、多くの人が連想するほど有名なのが「三角関数」ではないでしょうか。そしてその有名さに比例するように毛嫌いされているのではないでしょうか。
高校数学に出てくる非常にとっつきにくい項目です。ですが、表面だけでも一度理解すると、その利便性に驚かされます。それが証拠にこの考え方は、工業においても様々な場面で実用として利用されています。
では、この便利と思しき三角関数について基本的な説明をしていきます。またここでは基本的な内容ということで倍角や半角の扱いなどは割愛します。
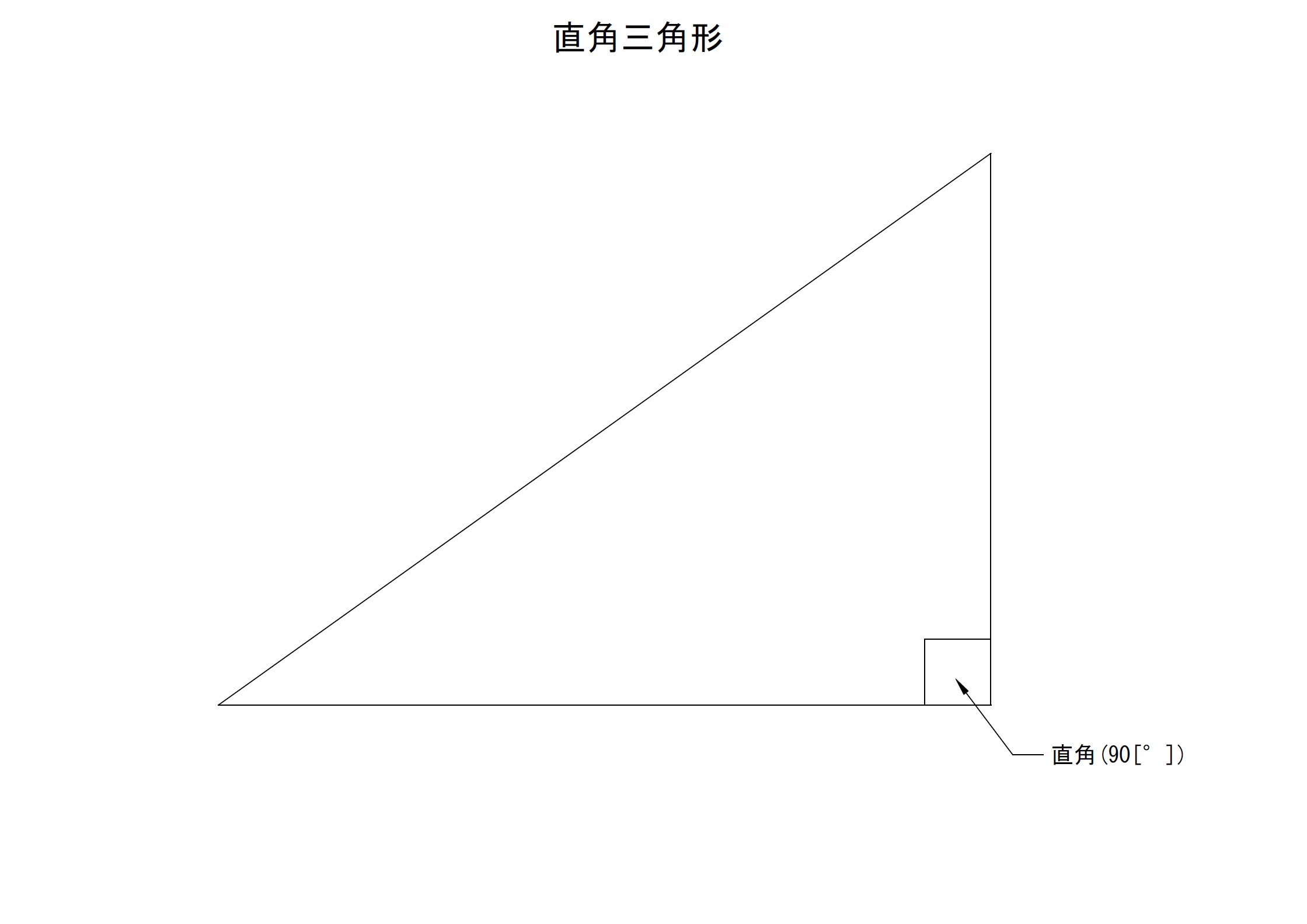
①直角三角形を前提とする
三角関数を説明するにあたって、述べておく必要があるのは基本的に「直角三角形」を対象としているということです。あくまでも「基本的」にということではあります。理由としては「正弦定理」や「余弦定理」という定理を用いれば必ずしも直角三角形でなくとも良い場合もあるからです。
しかしながら、「三平方の定理」や三角関数の基礎部分、また電気数学における「力率計算」では直角三角形を前提としています。まずは直角三角形を前提とした三角関数をきっちりと理解しましょう。
直角三角形は以下のような図形です。三角形の内角のひとつが必ず直角であることが条件です。
この直角三角形における、「各辺の長さの比」が三角関数の正体です。
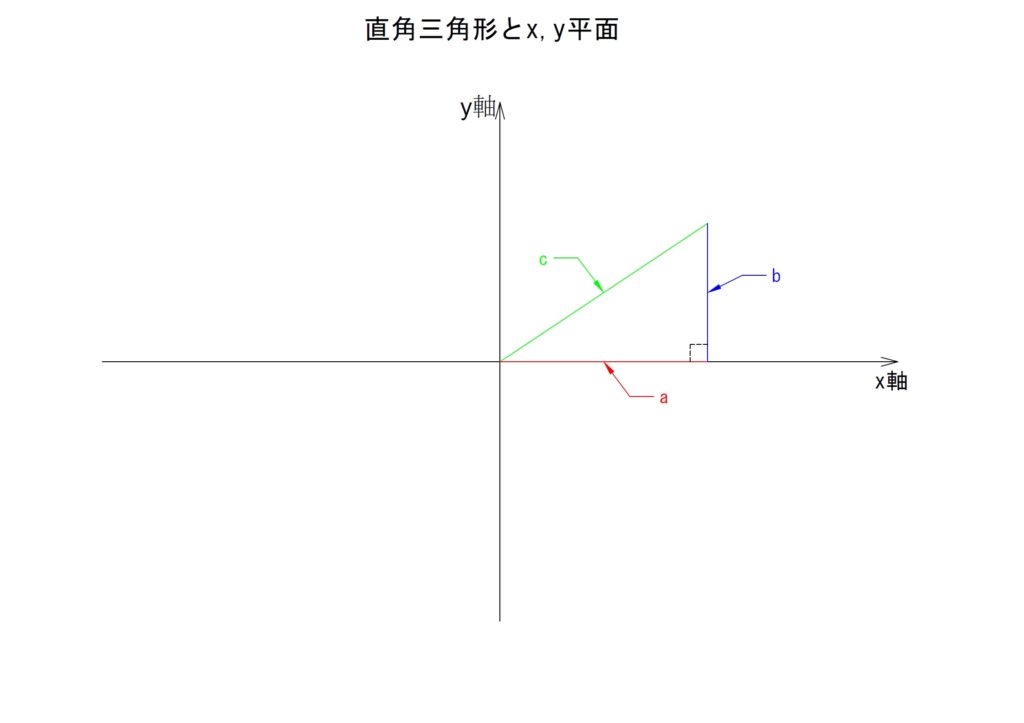
②各辺の長さの比
前述で「各辺の長さの比」と述べましたが、これだけでは「どんなときのどことどこの辺を比べた結果」なのかがわからないので以下に図示します。
まずは縦軸と横軸からなる平面が必要です。これに関しては、今までの関数と同じです。仮に縦軸を「y」とし、横軸を「x」とします。原点となる(0,0)の座標から任意の線をひきます。任意の線の端点に向かってx軸からの垂線を立ち上げます。各辺に「a」「b」「c」と記号を割り付けます。
このようにしてつくられた直角三角形に対して、各辺の長さがどのような比率になるかを求める計算式を、三角関数として扱います。
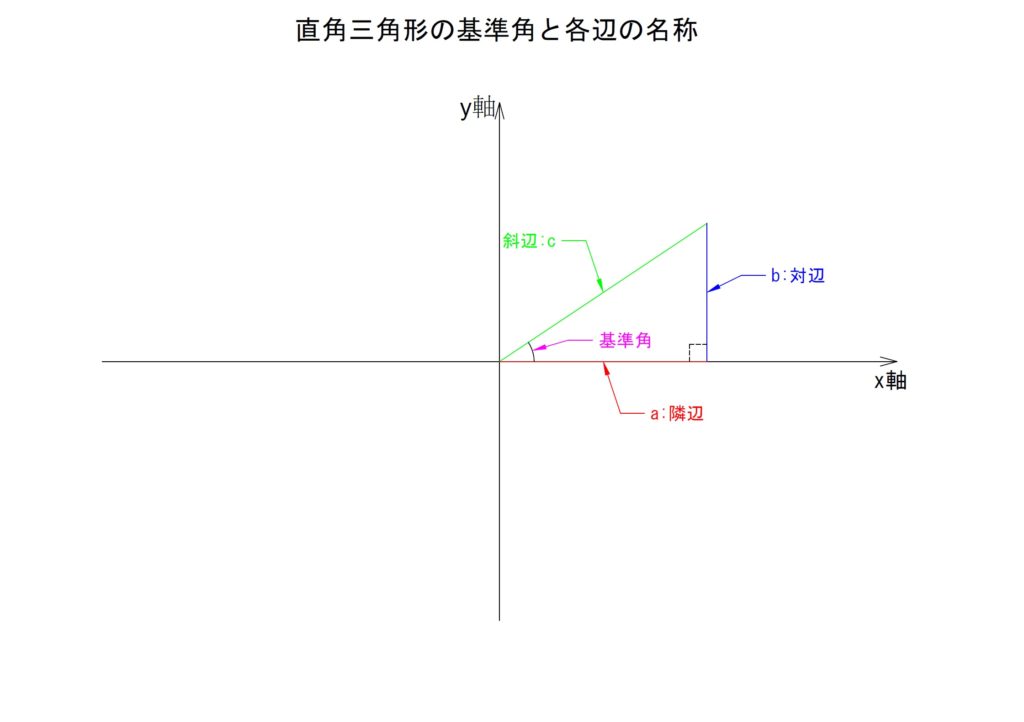
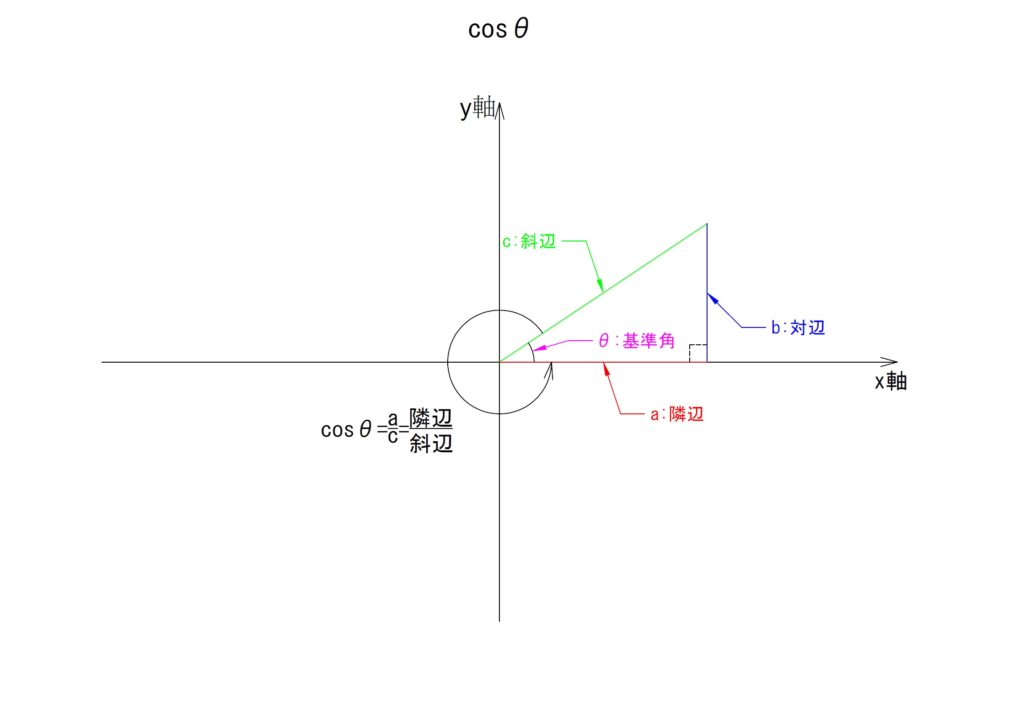
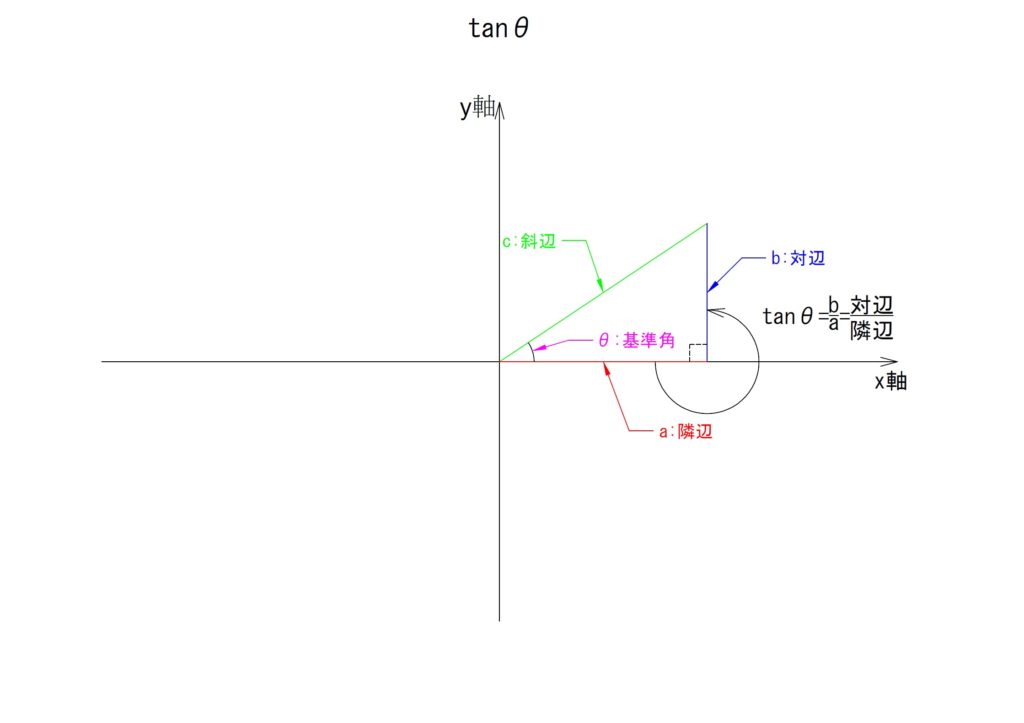
③斜辺,対辺,隣辺
三角関数における直角三角形では各辺に名称があります。各々「斜辺」「対辺」「隣辺」と名付けられています。では、これらの名称はどれがどれなのでしょうか。
これを知るためには先ず基準となる角を必要とします。基準となる角は「平面の原点を中心とし、横軸を「0°」として反時計回りに広がる角」になります。言葉で説明すると解りにくいですが、図で示すと一瞬です。下の図で示す角が基準となり、各辺の名称を決定します。
横軸に対して基準となる角をつくりだす斜めの一辺を「斜辺」といいます。
基準となる角の基(もと)となる横軸に沿う一辺はその角と隣り合うことから「隣辺」といわれます。
そして基準の角に相対する一辺を「対辺」といいます。
三角関数を扱うにあたって、基準となる角は必ず横軸からの角である必要があります。勝手に別の角を基準としてしまうと導かれる値は当然のことながら異なってしまいます。このことはしっかりおさえておくようにしましょう。
④sin,cos,tan
この見出しの文字を見ただけで「うわ〜(最悪…)」と感じる人も多いのではないでしょうか。
三角関数といえば、この記号です。「sin」は「サイン」の略号で「cos」は「コサイン」の略号、「tan」は「タンジェント」の略号となります。これに基準となる角の角度を示す記号である「θ(シータ)」や「φ(ファイ)」、または「ψ(プサイ)」などを組み合わせて表現することとなります。
例えば「sinθ」「cosφ」「tanψ」などです。必ず角度を表す記号とセットです。なお、これ以外に「sec(セカント)」「csc(コセカント)」「cot(コタンジェント)」という考え方もありますが、まずは「sin」「cos」「tan」の三つの概念をしっかり理解しましょう。
例えば基準となる角度を「θ」としたときの「sinθ」「cosθ」「tanθ」の各々の意味を、日本語と式そして図で表すと以下のようになります。前提として隣辺の長さを「a」とし、対辺の長さを「b」とし、斜辺の長さを「c」とします。
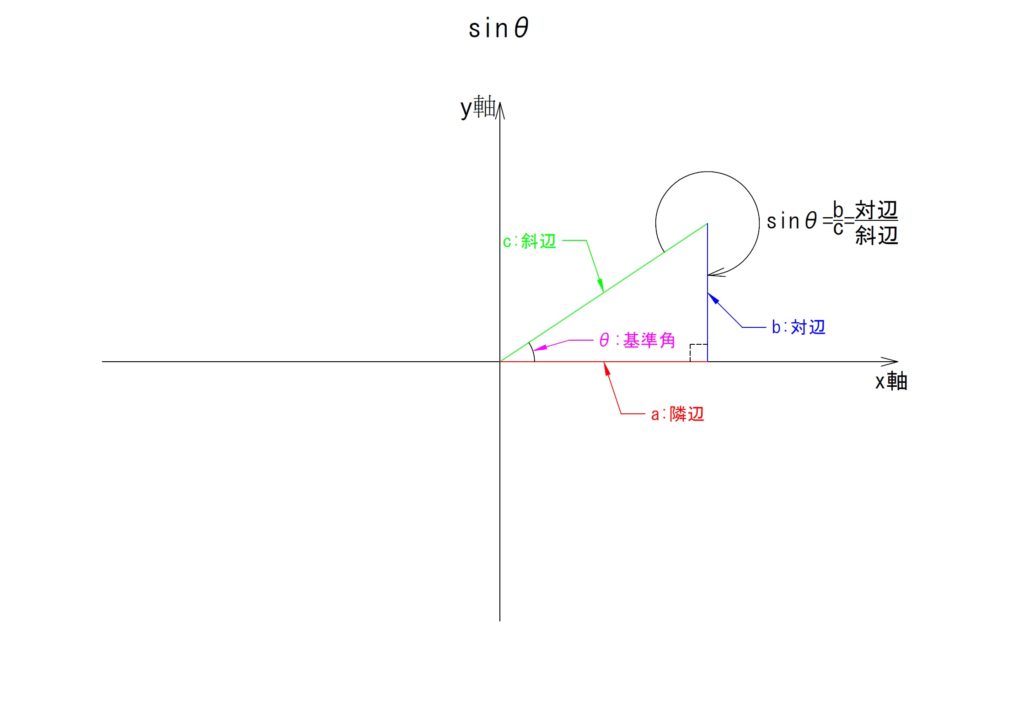
Ⅰ, sinθ
基準角「θ°」における斜辺に対する対辺の比
Ⅱ, cosθ
基準角「θ°」における斜辺に対する隣辺の比
Ⅲ, tanθ
基準角「θ°」における隣辺に対する対辺の比
上記の三つの例から、三角関数では基準となる角の角度がわかると各辺の長さの比が算出可能になるということがわかります。各辺の長さの比がわかったのであれば、どれか一辺の長さがわかった時点で残りの二辺の長さも算出可能となります。
⑤角度の表現
三角関数では角度の表現が二種類あります。その二種類は各々「度数法」と「弧度法」です。
度数法は一般によく利用される角度表現で、一周の角度を360°として表す方法です。
一方、弧度法は半径に対する弧の長さに着目した表現方法であり、さらに半径を「1」とする単位円では「角度」と「弧」が等しくなるという特徴を利用した角度表現方法です。
円周の長さは「2πr」により算出可能であることを算数の授業で習いますが、このとき「r=1」つまり単位円であれば一周の長さは「2π」となります。つまり「360°」は「2π」であるといえます。そして角度を「2π」とするときの単位は「rad(ラジアン)」となります。
このことを利用するとその他の角度について以下の例のように表現することが可能となります。





この弧度法は三角関数ではよく利用される表現であるため、しっかりおさえておかなければ、三角関数の理解が難しくなります。
しかし、なぜこのような別の視点の角度表現を利用するのでしょうか。弧度法によりどんなメリットが得られるのでしょうか。これについて簡単に端的に述べると、「角度を長さの一つとして考えることが可能になる」というメリットがあります。このことから三角関数における微分等の計算において式の単純化が図れるという恩恵が受けられます。
⑥三角関数のグラフ化
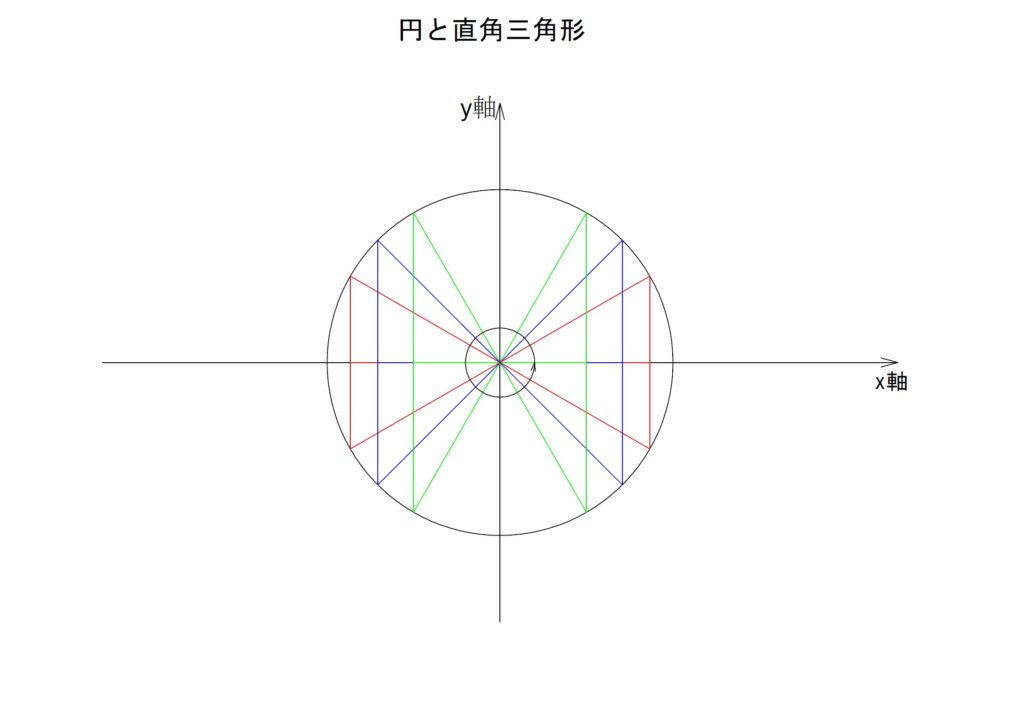
ここから三角関数のグラフ化について説明しますが、これまでにも述べたとおり三角関数には「sin」「cos」「tan」と基本的なものでも3パターンがあります。ひとつずつ説明しますが、まずは下の図を見てください。
三角関数は直角三角形を前提とするということを先に述べましたが、「円」とも深いつながりがあります。
斜辺を半径とする単位円において横軸と斜辺が成す角を「θ」とします。三角関数は任意の角「θ」における各辺の比ですので、「sin」「cos」「tan」のいずれにおいても繰り返し同じ値を計上することになります。
つまり三角関数のグラフは、繰り返される円の動きの中で、任意の角度で形成される直角三角形の各辺の比を表現していることとなります。
上記を踏まえて一つずつグラフ化していきます。なお、グラフ化において独立変数が角度であることから、「x」ではなく「θ」を用います。それに伴い従属変数も「y」ではなく「γ(ガンマ)」を用います。この記号を用いることに特別な意味はありません。ただ、「x」「y」を変数として用いると三角関数が「角度」と「辺の比」による関数であることが見えづらくなると考えた結果、別の記号をあてたというだけです。「γ=f(θ)」となります。
Ⅰ,γ=sinθ
「γ」が、ある値の間を行ったり来たりするグラフとなっていることが見てとれます。、「γ」は直角三角形の斜辺と対辺の比ですので「-1」と「1」の間を行き来することとなります。
このようなグラフには名前がついており「正弦波」や「正弦曲線」また「サインカーブ」とよばれます。
Ⅱ,γ=cosθ
「γ=sinθ」のグラフを「π/2」(90°)だけ紙面左側にずらしたグラフになります。「γ」は直角三角形の斜辺と隣辺の比ですので「sinθ」のときと同様に「-1」と「1」の間を行き来することとなります。
この曲線のことを正確には「余弦波」や「余弦曲線」または「コサインカーブ」とよぶのでしょうが、形としては正弦波と同じなので、まとめて正弦波やサインカーブなどとよばれることが多いです。
Ⅲ,γ=tanθ
「sinθ」や「cosθ」の場合とは大きく見た目の異なるグラフとなっています。先ほどまでは斜辺に対する隣辺や対辺の比でしたので「γ」が「-1」と「1」の間を行き来する形のグラフとなりましたが、今回はそのようにならずS字を描くような形になります。注意すべきは「対辺/隣辺」が「0/a」となることはあっても「a/0」はあり得ないというところです。数学において分数の分母「0」は定義できません。隣辺が限りなく「0」に近づくとき対辺との比は限りなく大きくなるということであり、それはこのグラフが漸近線をもつということを意味します。そしてある角度(ここでは「π/2」)を境に「γ」の値は逆方向(負方向)へ転換し、以降これを繰り返すということになります。
4.ベースになる知識
今回は「方程式」と「関数」という内容について説明をしました。これらは数学でも基礎となる知識であると同時に、電気の分野においても理解していることを前提とされる項目です。
方程式から「解」を導き出すという作業は、電気の実務においては容量計算や電流算出の他、非常に多岐にわたる場面で使用することとなります。これの利用方法がわからないということは、電気の特に技術的な業務に携わることが非常に困難であるということとほぼ同義になってしまいます。
さらにいうと、方程式は日常生活でも時間計算や距離計算,支払いや収入の計算(割増・割引は顕著な例です),スコアや確率の計算など、実は様々なケースで利用されます。意識せず使っていることも多いのではないでしょうか。
また関数は、事象を数値化しさらに可視化することでこの先に起こりうる現象を予測したり、コントロールすることに用いられます。多くは物理学や工学での応用ではないでしょうか。もちろん確率統計の分野や経済などでも用いられることはあるでしょう。
電気の分野でも様々なところで関数が出てきます。なにかを制御しようとするときに、関数を用いた計算の結果に基づいて、制御対象へのアクションを決定するということが多々あります。また、安全を目的とした制御などでは、安全動作へ移行する閾(しきい)値自体に関数を設定し、異常状態の度合いによってアウトプットを決定するというものもあります。そもそも交流回路においては非常に早い段階で関数の理解を求められることになります。電気の世界は関数と非常に密接であるといえます。
以上、「方程式」と「関数」について説明しました。掘り下げれば掘り下げるほど、それこそ指数関数的に難易度があがる数学ですが、自身に必要な知識であるならば諦めず習得を目指すべきであると筆者は考えます。同時に、そのための行程すら無駄にならないとも考えています。筆者もまだまだ未熟ですが共に邁進しましょう!